Imenovalec geometrijske progresije: formule in lastnosti
Geometrijska progresija, skupaj z aritmetiko, je pomembna numerična serija, ki jo preučujemo v tečaju algebre v 9. razredu. V tem članku upoštevamo imenovalec geometrijskega napredovanja in kako njegova vrednost vpliva na njegove lastnosti.
Opredelitev napredovanja geometrijskega
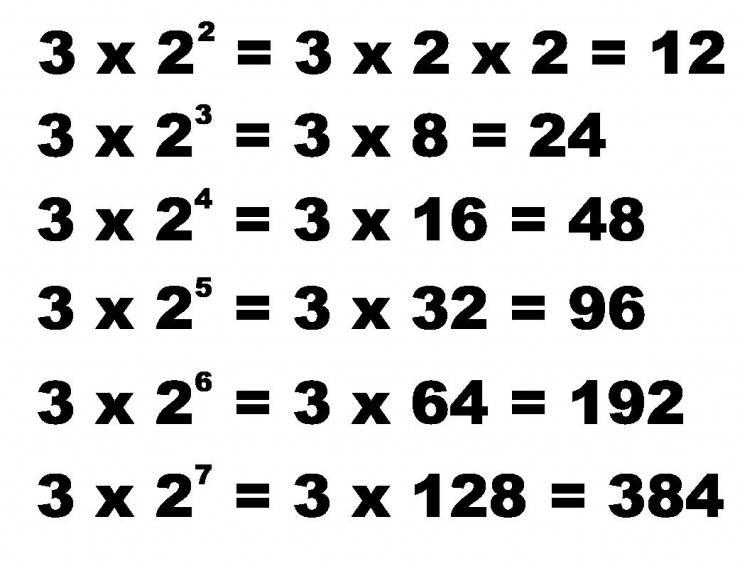
Za začetek bomo podali definicijo tega števila. Takšna vrsta racionalnih števil, ki se oblikuje z zaporednim množenjem njenega prvega elementa s konstantnim številom, imenovanim imenovalec, se imenuje geometrijska progresija.
Na primer, številke v vrsticah 3, 6, 12, 24, ... so geometrijska progresija, ker če pomnožimo 3 (prvi element) z 2, dobimo 6. Če se 6 pomnoži z 2, dobimo 12, in tako naprej.
Člani obravnavanega zaporedja so običajno označeni s simbolom a i , kjer je i celo število, ki označuje število elementa v seriji.
Zgornja definicija napredovanja je lahko napisana v jeziku matematike na naslednji način: a n = b n-1 * a 1 , kjer je b imenovalec. To formulo lahko enostavno preverimo: če je n = 1, potem b 1-1 = 1 in dobimo 1 = a 1. Če je n = 2, potem a n = b * a 1 in spet pridemo do definicije obravnavane serije številk. . Podobne argumente je mogoče nadaljevati pri velikih vrednostih n.
Imenovalec napredovanja geometrijskega
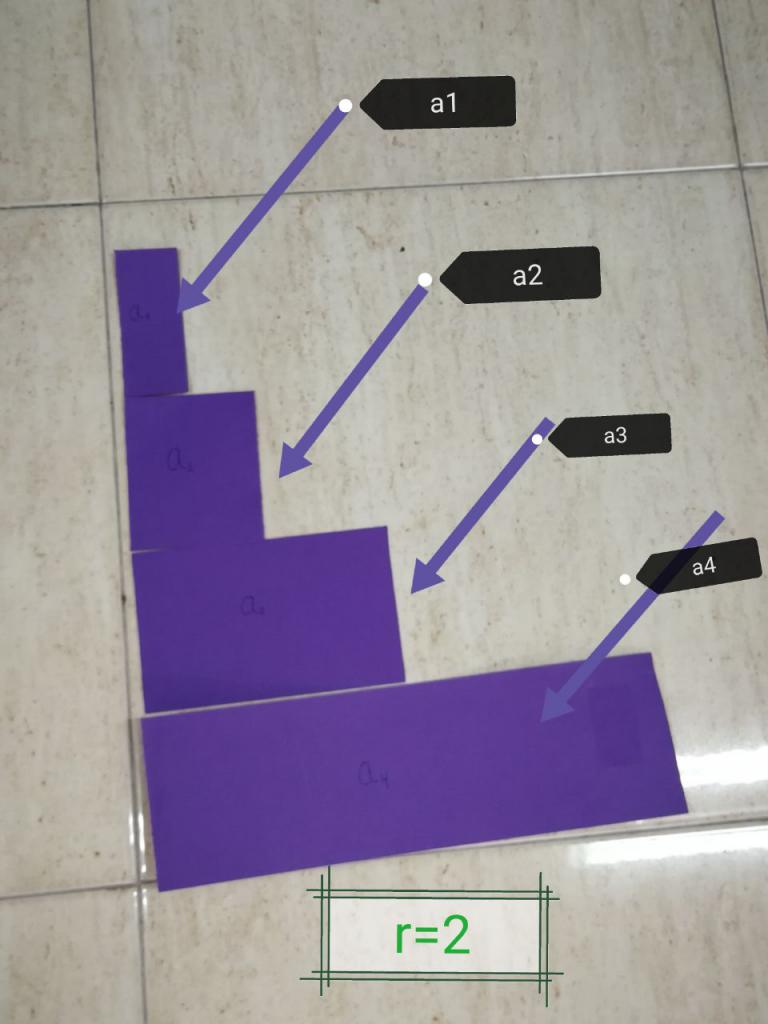
Številka b v celoti določa naravo celote številnih serij. Imenovalec b je lahko pozitiven, negativen in ima tudi vrednost, večjo od ene ali manj. Vse te možnosti vodijo do različnih zaporedij:
- 1. Število racionalnih števil je vedno večje. Na primer 1, 2, 4, 8, ... Če je element a 1 negativen, se bo celotno zaporedje povečalo le v absolutni vrednosti, vendar se bo zmanjšalo glede na znak števila.
- b <-1. V tem primeru govorimo o spremenljivi seriji, kar pomeni, da se bodo sosednji elementi razlikovali v znaku. Na primer 1, -2, 4, -8, 16, ...
- -1 <b <1. To je poseben primer, ki ima svoje ime - padajoče neskončno geometrijsko napredovanje. Njegova glavna značilnost je, da se, ne glede na znak imenovalca, nagiba k določeni končni vsoti, ko doda neskončno število njenih elementov.
- b = 1. Pogosto se takšen primer ne imenuje napredovanje, saj obstaja običajna vrsta enakih racionalnih števil. Na primer, -4, -4, -4.
Formula za vsoto
Preden preidemo na obravnavo posebnih nalog z uporabo imenovalca zadevnega tipa napredovanja, je treba podati pomembno formulo za vsoto svojih prvih n elementov. Formula ima obliko: S n = (b n - 1) * a 1 / (b - 1).
Ta izraz lahko dobite sami, če upoštevate rekurzivno zaporedje članov napredovanja. Upoštevajte tudi, da je v zgornji formuli dovolj vedeti le prvi element in imenovalec, da bi našli vsoto poljubnega števila članov.
Brezstopenjsko zmanjševanje zaporedja
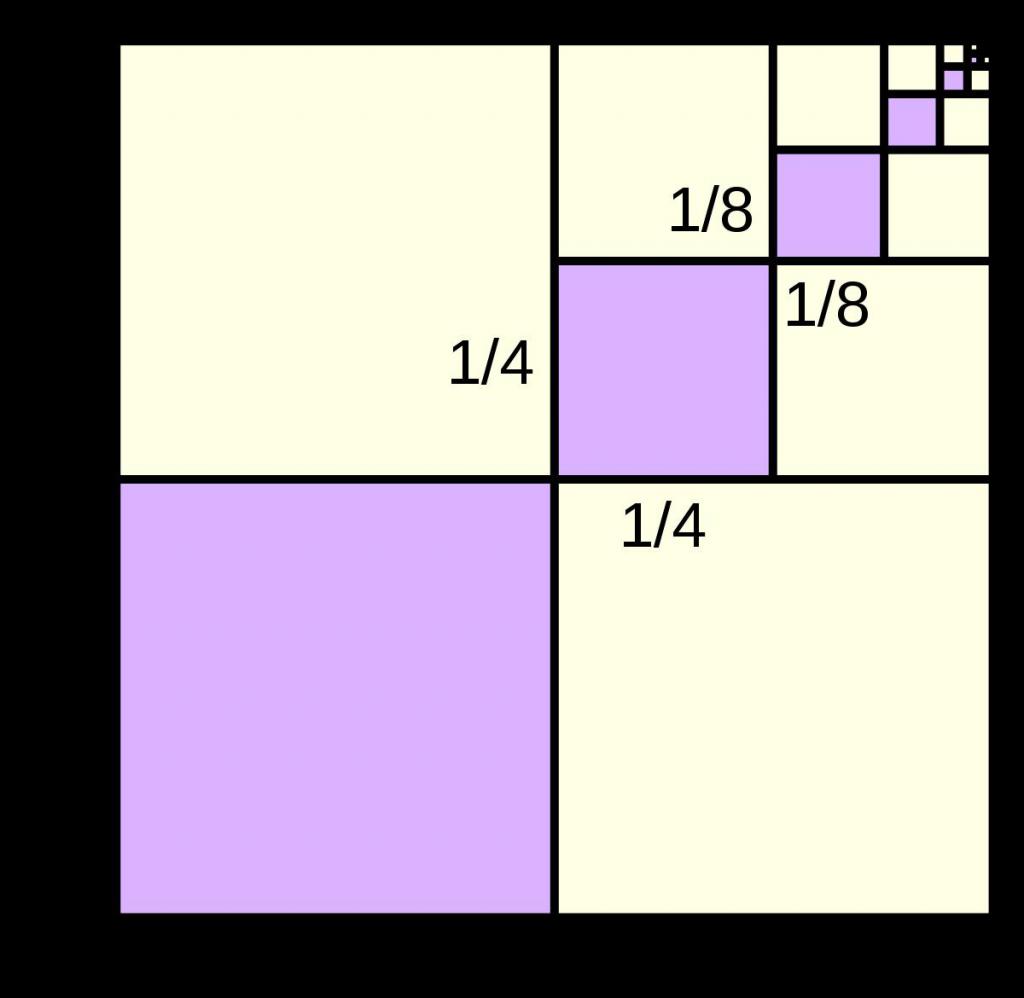
Zgoraj je bilo razloženo, kaj je. Zdaj, ko poznamo formulo za S n , jo uporabimo za to število števil. Ker vsako število, katerega modul ne presega 1, se nagiba k ničli, ko je postavljen na velike stopinje, to je, b> => 0, če -1 <b <1 (| b | <1), potem se splošna formula za vsoto pretvori v naslednji izraz: S a = a 1 / (1 - b).
Ker je razlika (1 - b) vedno pozitivna, ne glede na vrednost imenovalca, je znak vsote padajočega neskončnega napredovanja geometrijskega S ∞ edinstveno določen z znakom njegovega prvega elementa a 1 .
Zdaj bomo obravnavali več nalog, kjer bomo pokazali, kako uporabiti znanje, pridobljeno na konkretnih številkah.
Številka problema 1. Izračun neznanih elementov napredovanja in zneska
Glede na napredovanje geometrijskega, imenovalca napredovanja 2 in njegovega prvega elementa 3. Kaj bodo njegovi 7. in 10. člani enaki in kaj je vsota njegovih sedmih začetnih elementov?
Pogoj problema je preprost in vključuje neposredno uporabo zgornjih formul. Torej, da izračunamo element s številom n, uporabimo izraz a n = b n-1 * a 1 . Za sedmi element imamo: a 7 = b 6 * a 1, ki nadomesti znane podatke, dobimo: a 7 = 2 6 * 3 = 192. Na enak način nadaljujemo za 10. član: a 10 = 2 9 * 3 = 1536 .
Uporabimo dobro znano formulo za vsoto in to vrednost določimo za prvih 7 elementov serije. Imamo: S 7 = (2 7 - 1) * 3 / (2 - 1) = 381.
Problemska številka 2. Določanje vsote poljubnih elementov napredovanja
Naj -2 je enaka imenovalcu napredovanja v geometrijskem napredovanju b n-1 * 4, kjer je n celo število. Potrebno je določiti znesek od 5. do 10. elementa te serije.
Zastavljenega problema ni mogoče rešiti neposredno z znanimi formulami. To je mogoče rešiti z dvema različnima metodama. Za popolnost vam bomo dali oboje.
Metoda 1. Njegova zamisel je preprosta: potrebno je izračunati dve ustrezni vrednosti prvih članov in nato odšteti drug od drugega. Izračunamo manjšo vsoto: S 10 = ((-2) 10 - 1) * 4 / (-2 - 1) = -1364. Zdaj izračunamo veliko količino: S 4 = ((-2) 4 - 1) * 4 / (-2 - 1) = -20. Upoštevajte, da so se v zadnjem izrazu seštevali le štirje izrazi, saj je peti že vključen v vsoto, ki jo je treba izračunati s pogojem problema. Na koncu vzemite razliko: S 5 10 = S 10 - S 4 = -1364 - (-20) = -1344.
Metoda 2. Preden nadomestite številke in štetje, lahko dobite formulo za vsoto med člani m in n obravnavane serije. Delujemo na enak način kot v metodi 1, delamo le najprej s simbolično predstavitvijo vsote. Imamo: S n m = (b n - 1) * a 1 / (b - 1) - (b m - 1 - 1) * a 1 / (b - 1) = a 1 * (b n - b m - 1 ) / (b - 1). Znane številke lahko nadomestite z dobljenim izrazom in izračunate končni rezultat: S 10 5 = 4 * ((-2) 10 - (-2) 4 ) / (-2 - 1) = -1344.
Problemska številka 3. Kaj je imenovalec?

Naj bo a 1 = 2, poiščimo imenovalec napredovanja geometrične, pod pogojem, da je njena neskončna vsota 3, in je znano, da je to padajoči niz številk.
S težavo problema ni težko uganiti, katero formulo je treba uporabiti za njeno reševanje. Seveda se vsota napredovanja neskončno zmanjšuje. Imamo: S ∞ = a 1 / (1 - b). Iz kje izrazimo imenovalec: b = 1 - a 1 / S ∞ . Še vedno je treba nadomestiti znane vrednosti in pridobiti zahtevano število: b = 1 - 2/3 = -1 / 3 ali -0.333 (3). Ta rezultat je mogoče kvalitativno preveriti, če se spomnimo, da za to vrsto zaporedja modul b ne sme preseči 1. Kot je razvidno, | -1 / 3 | <1.
Problemska številka 4. Izterjava vrste številk
Naj navedemo 2 elementa numeričnega niza, npr. 5. je 30, deseta pa 60. Iz teh podatkov je treba celotno serijo rekonstruirati, vedoč, da izpolnjuje lastnosti geometrijske progresije.
Za rešitev problema je potrebno začeti pisati ustrezen izraz za vsakega znanega člana. Imamo: a 5 = b 4 * a 1 in a 10 = b 9 * a 1 . Zdaj delimo drugi izraz v prvi, dobimo: a 10 / a 5 = b 9 * a 1 / (b 4 * a 1 ) = b 5 . Zato določimo imenovalec, pri čemer vzamemo koren pete stopnje iz razmerja izrazov, znanih iz pogoja problema, b = 1.148698. Nastalo število se nadomesti v enega od izrazov za znani element, dobimo: a 1 = a 5 / b 4 = 30 / (1,148698) 4 = 17.2304966.
Tako smo našli, kaj je imenovalec napredovanja bn enak, in geometrijsko napredovanje b n-1 * 17,2304966 = a n , kjer je b = 1,148698.
Kje se uporablja geometrijska progresija?

Če v praksi ne bi bilo uporabe te številske serije, bi se njena študija zmanjšala na čisto teoretični interes. Vendar taka vloga obstaja.

Spodaj so trije najbolj znani primeri:
- Paradoks Zenoja, v katerem spreten Ahil ne more dohiteti počasne želve, je rešen s konceptom zmanjševanja neskončnega zaporedja števil.
- Če na vsako celico šahovnice položite žitno zrnje, položite 1 žito na prvo celico, 2 na 2., 2. na 3. in tako naprej, potem potrebujete 18446744073709551615 zrn, da zapolnite vse celice plošče!
- V igri "Tower of Hanoi", da bi preuredili diske od enega palice do drugega, je potrebno izvesti 2 n - 1 operacij, kar pomeni, da njihovo število eksponentno narašča s številom uporabljenih diskov n.