Korelacijski koeficient in vzročna povezava: formule in njihova interpretacija

Korelacijski koeficient je stopnja povezave med dvema spremenljivkama. Njegov izračun daje idejo, ali obstaja odvisnost med dvema podatkovnima nizoma. Za razliko od regresije korelacija ne omogoča predvidevanja vrednosti količin. Vendar je izračun koeficienta pomemben korak v predhodni statistični analizi. Ugotovili smo, da je korelacijski koeficient med stopnjo neposrednih tujih naložb in stopnjo rasti BDP visoka. To nam daje idejo, da je za zagotovitev blaginje potrebno ustvariti ugodno okolje za tuje podjetnike. Na prvi pogled ni tako očiten zaključek!

Korelacija in vzročnost

Morda ni nobenega statističnega področja, ki bi bilo tako trdno uveljavljeno v našem življenju. Korelacijski koeficient se uporablja na vseh področjih javnega znanja. Njena glavna nevarnost je v tem, da se njene visoke vrednote pogosto špekulirajo, da bi prepričali ljudi in jih prepričali v nekatere sklepe. Dejansko pa močna korelacija sploh ne kaže na vzročno zvezo med količinami.

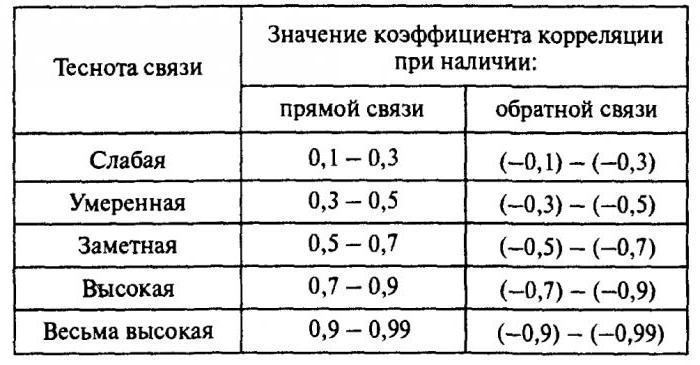
Korelacijski koeficient: Pearsonova in Spearmanova formula

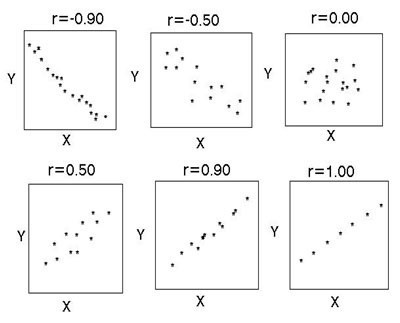
Obstaja več ključnih kazalnikov, ki označujejo razmerje med dvema spremenljivkama. V zgodovini je prvi Pearsonov linearni korelacijski koeficient. Še vedno je v šoli. Razvili so ga C. Pearson in J. Yul na podlagi del Fr. Galton. Ta koeficient vam omogoča, da vidite razmerje med racionalnimi številkami, ki se racionalno spreminjajo. Vedno je večji od -1 in manj kot 1. Negativno število pomeni obratno sorazmerno odvisnost. Če je koeficient nič, potem ni povezave med spremenljivkami. Enako pozitivnemu številu - obstaja proporcionalno razmerje med preučevanimi količinami. Spearmanov koeficient korelacije ranga vam omogoča, da poenostavite izračune z izgradnjo hierarhije spremenljivih vrednosti.

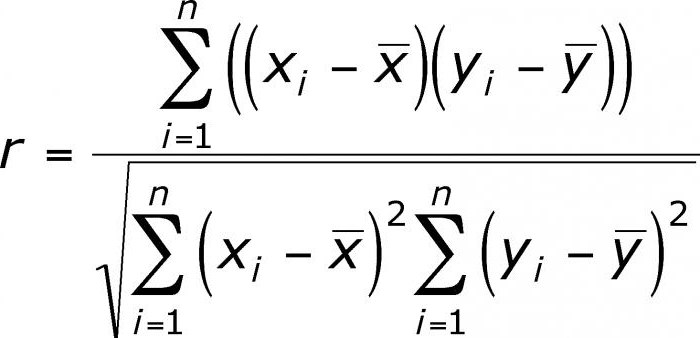
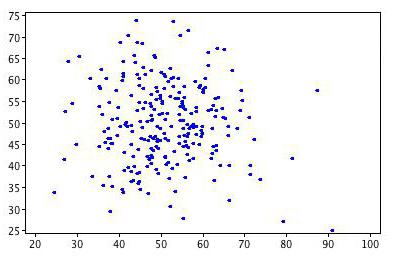
Razmerje med spremenljivkami

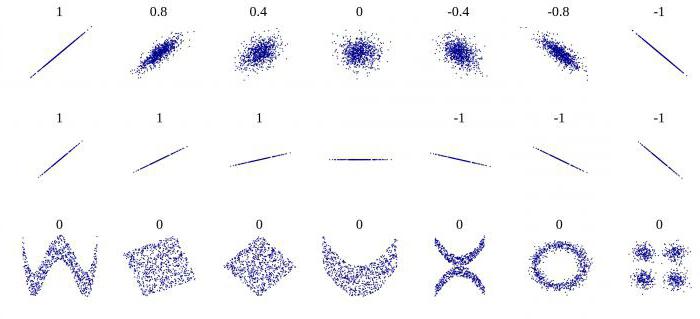
Korelacija pomaga najti odgovor na dve vprašanji. Prvič, ali je razmerje med spremenljivkami pozitivno ali negativno. Drugič, kako močna je odvisnost. Korelacijska analiza je močno orodje, s katerim lahko dobite te pomembne informacije. Preprosto je videti, da družinski prihodki in odhodki padajo in rastejo sorazmerno. To razmerje velja za pozitivno. Nasprotno, z rastjo cen blaga se povpraševanje po njem zmanjšuje. Takšna povezava se imenuje negativna. Vrednosti korelacijskega koeficienta so v razponu med -1 in 1. Nič pomeni, da med preučevanimi vrednostmi ni povezave. Čim bližje je indikator do skrajnih vrednosti, tem močnejša je povezava (negativna ali pozitivna). Odsotnost odvisnosti je prikazana s koeficientom od -0,1 do 0,1. Treba je razumeti, da taka vrednost pomeni le odsotnost linearne povezave.

Funkcije aplikacije

Uporaba obeh kazalnikov je odvisna od določenih predpostavk. Prvič, prisotnost močne povezave ne pomeni, da ena količina določa drugo. Lahko obstaja tudi tretja količina, ki opredeljuje vsakega od njih. Drugič, visok Pearsonov korelacijski koeficient ne kaže na vzročno zvezo med proučevanimi spremenljivkami. Tretjič, kaže le linearno odvisnost. Korelacija se lahko uporabi za oceno pomembnih kvantitativnih podatkov (npr. Atmosferskega tlaka, temperature zraka) in ne kategorije, kot so spol ali najljubša barva.

Koeficient večkratne korelacije

Pearson in Spearman sta raziskala razmerje med dvema spremenljivkama. Toda kako ukrepati v primeru, da so tri ali celo več. Tukaj rešuje večkratni korelacijski koeficient. Na primer, na bruto nacionalni proizvod ne vplivajo le neposredni tujih naložb pa tudi denarne in fiskalne politike in ravni izvoza. Stopnja rasti in obseg BDP sta posledica interakcije več dejavnikov. Vendar je treba razumeti, da model večkratne korelacije temelji na številnih poenostavitvah in predpostavkah. Prvič, multikolinearnost med količinami je izključena. Drugič, razmerje med odvisnimi in spremenljivkami, ki vplivajo nanj, naj bi bilo linearno.

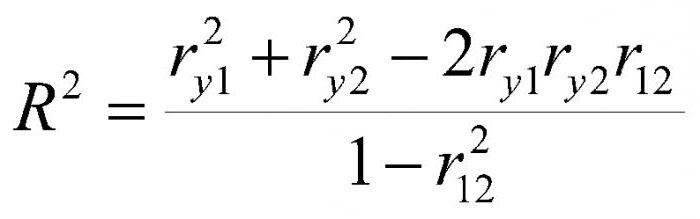
Področja uporabe korelacijske in regresijske analize

Ta metoda ugotavljanja razmerja med količinami se pogosto uporablja v statistiki. Najpogosteje se uporablja v treh glavnih primerih:

1. Preizkusite vzročno zvezo med vrednostmi dveh spremenljivk. Zato raziskovalec upa, da bo našel linearno razmerje in izpeljal formulo, ki opisuje ta razmerja med količinami. Enote njihovih meritev so lahko drugačne.
2. Preverjanje povezave med vrednostmi. V tem primeru nihče ne določi, katera spremenljivka je odvisna. Lahko se izkaže, da vrednost obeh količin povzroča nek drug dejavnik.
3. Za izpeljavo enačbe. V tem primeru lahko preprosto nadomestite številke v njem in ugotovite vrednosti neznane spremenljivke.

Človek, ki išče vzročno zvezo

Zavest je urejena tako, da moramo vsekakor razložiti dogodke, ki se dogajajo. Oseba vedno išče povezavo med sliko sveta, v katerem živi, ​​in informacijami, ki jih prejme. Pogosto možgani ustvarjajo red iz kaosa. Zlahka vidi vzročno zvezo, kjer je ni. Znanstveniki se morajo posebej naučiti premagati ta trend. Sposobnost ocenjevanja razmerja med podatki je objektivno potrebna v akademski karieri.

Medijska pristranskost

Razmislite o tem, kako lahko napačno razložite prisotnost korelacijske povezave. Skupina britanskih študentov s slabim vedenjem je bila vprašana, ali so njihovi starši kadili. Potem je bil test objavljen v časopisu. Rezultat je pokazal močno povezavo med kajenjem staršev in kaznivimi dejanji njihovih otrok. Profesor, ki je vodil to študijo, je celo predlagal opozorilo na cigaretne pakete. Vendar pa je s tem sklepom veliko težav. Prvič, korelacija ne kaže, katera od količin je neodvisna. Zato lahko domnevamo, da je zasvojenost staršev posledica neposlušnosti otrok. Drugič, nemogoče je z gotovostjo trditi, da se oba problema ne pojavita zaradi tretjega dejavnika. Na primer, družine z nizkimi dohodki. Treba je omeniti čustveni vidik začetnih ugotovitev profesorja, ki je opravil študijo. Bil je goreč nasprotnik kajenja. Zato ni presenetljivo, da je rezultate svojih raziskav interpretiral na ta način.

Sklepi

Napačna razlaga korelacije kot vzročne povezave med dvema spremenljivkama lahko povzroči sramotne napake v raziskavah. Problem je v tem, da leži v samem središču človeške zavesti. Na tej posebni funkciji temeljijo številni marketinški triki. Razumevanje razlike med vzročnostjo in korelacijo omogoča racionalno analizo informacij tako v vsakdanjem življenju kot v poklicni karieri.