Kaj je to - stožec v geometriji. Ravni stožec z okroglo osnovo in njegovimi lastnostmi

Prostorska geometrija, katere potek poteka v srednji šoli, preučuje značilnosti in lastnosti različnih geometrijskih oblik v treh dimenzijah. Ena od takih znanih številk je stožec. Članek bo odgovarjal na ta vprašanja, da je to stožec, katere elemente opisuje in katere lastnosti ima.

Konus v geometriji

Z vidika stereometrije je stožec figura, ki se oblikuje v prostoru s povezovanjem ravnih segmentov določene točke z krivuljo v ravnini. Ta krivulja se imenuje directrix, ali vodnik. Omejuje obliko podlage. Directrix je lahko zaprta črta, kot je elipsa ali krog, ali pa ni zaprta, kot hiperbola ali parabola. Vsi segmenti, ki povezujejo directrix z zgoraj omenjeno točko prostora, se imenujejo generatri, ali generatorji. Skupina generatorjev definira stožčasto površino, točka, iz katere izstopajo, pa se imenuje vozlišče stožca.

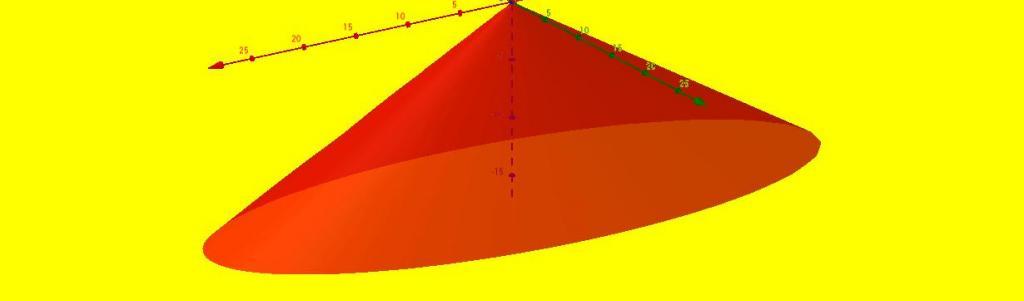
Tako je stožec figura, ki ima eno točko, brez robov, in je sestavljena iz dveh površin (ploska podlaga in stranska stožčasta površina). Eliptični stožec je prikazan na zgornji sliki.

Krožni ali okrogli stožec

Pod besedo "krog" v naslovu elementa razumejo sliko, katere osnovo je krog. Za razliko od drugih tipov stožca se lahko zaradi vrtenja dobi okrogla slika. Spodnja slika prikazuje ta postopek.

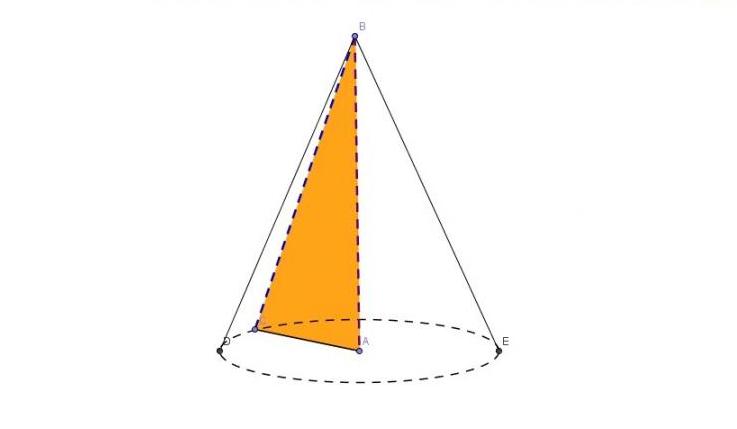
Naj na kratko pojasnimo, kaj prikazuje slika. Trikotnik ABC je pravokoten. Če se obrne okoli noge AB, bo noga AC opisala eno površino stožca, bazo in hipotenuza BC, ki bo povzročila nastanek stožčaste površine zaradi rotacije.

Stožec, prikazan na sliki, ni samo okrogel, temveč tudi raven. Slednje je pomembno upoštevati pri izračunih linearnih parametrov, površine in volumna slike.

Geometrijska oblika stožca je ravna, če višina h pade točno v središče podnožja (v tem primeru je višina segment AB in središče podstavka je točka A). Če določen pogoj ni izpolnjen, se številka imenuje poševna. Za jasnost so spodaj prikazani poševni in ravni konusi.

Mnogi predmeti, ki nas obdajajo, kot so sladoledni stožci, črtasti cestni stožec ali lijak za nalivanje tekočine skozi ozke odprtine, imajo stožčasto obliko z okroglo osnovo.

Nato upoštevamo kvantitativne značilnosti ravnega stožca z okroglo osnovo.

Linearne dimenzije figure in kota na dnu

Linearne dimenzije stožca so niz parametrov, ki vam omogočajo, da enolično določite sliko v prostoru. Ti so naslednji:

• osnovni radij r;
• višina h;
• generatrix g.

Ugotavljamo, da so pri obravnavani vrsti stožca vsi generiki enaki drug drugemu in sekajo podnožje pod enakim kotom.

Poleg zgornjih linearnih parametrov je za stožec značilen tudi kot φ med generatorjem in bazo.

Vse te značilnosti so med seboj povezane z naslednjimi osnovnimi enačbami:

g = √ (h ² + r ² );

g = h / sin (φ);

g = r / cos (φ);

h = r * tg (φ)

Te enakosti lahko zapišemo samostojno, če upoštevamo pravokotni trikotnik v notranjosti stožca in se spomnimo definicij navedenih trigonometričnih funkcij.

Površina

Območje osnove in stožčaste površine je pomembna značilnost stožca. Bolj jasno in lažje je preučiti površino figure ne v tridimenzionalnem, temveč v dvodimenzionalnem prostoru. Za to naredite tako imenovane vzorce skeniranja. Proces njegovega prejemanja si lahko predstavljate takole: Recimo, da je stožec narejen iz papirja. Najprej odrežemo njeno podlago vzdolž oboda in nato odrežemo konično površino vzdolž generatorja in jo odvijemo. Prejeli smo skeniranje stožca, ki je prikazan spodaj na sliki.

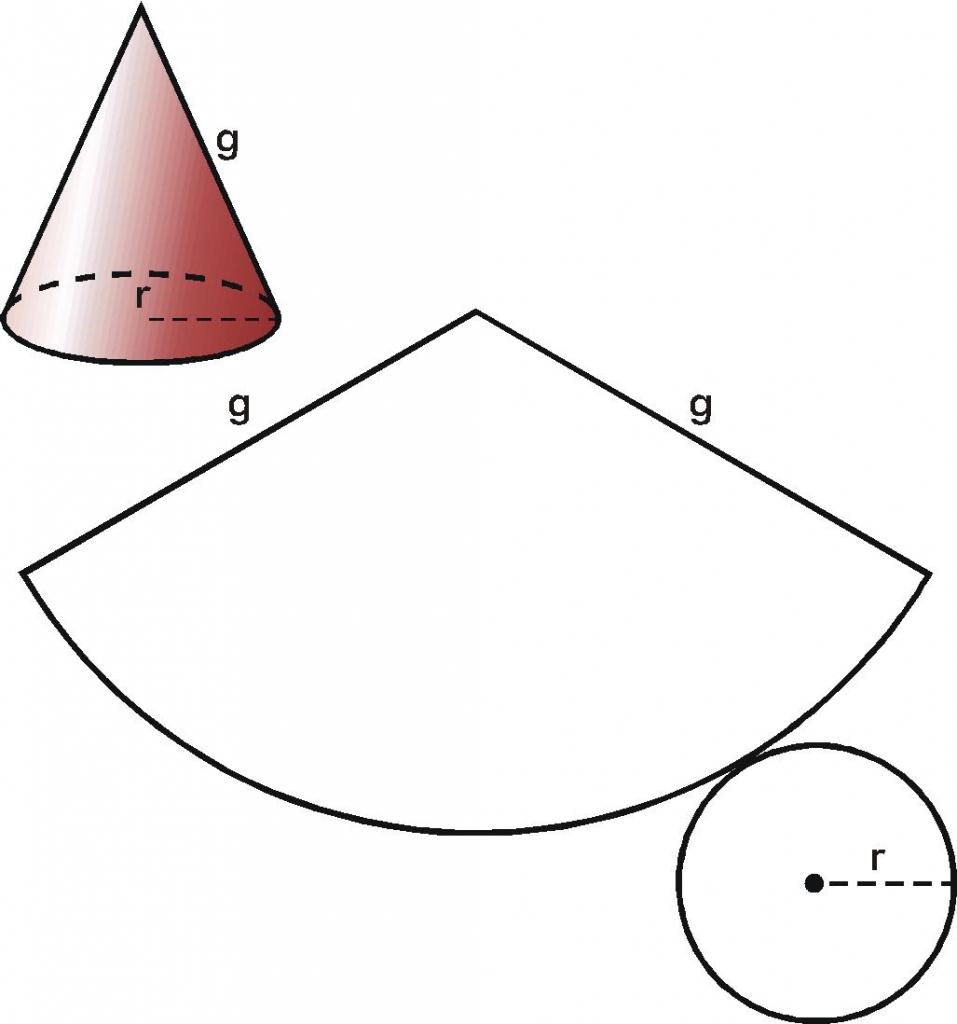
Območje celotnega čiščenja S je enako:

S = S _o + S _b

Če je prvi izraz (S _o ) območje kroga, je drugi izraz (S _b ) območje krožnega sektorja, ki odraža stožčasto površino. Vrednost S _{o se} izračuna po naslednji formuli:

S _o = pi * r ²

Pri krožnem sektorju so razmere bolj zapletene. Omejen je z dvema polmeroma, katerih dolžina je enaka generatriki g, in en lok, ki ustreza obodu osnovnega kroga. Te številčne informacije vam omogočajo, da enolično določite področje sektorja. Ne bomo šli v matematične izračune, ampak bomo takoj podali končno formulo za S _b :

S _b = pi * r * g

Primerjava zapisanih formul za S _b in S _o kaže, da je stranska površina vedno večja od tiste za bazo z g / r.

Formula za skupno površino je naslednja:

S = pi * r * (r + g)

Velikost telesa

Stožec je prostorska figura, zato ima določen volumen. Številčno ustreza površini prostora, ki je omejena s konično površino in krožno osnovo. Za določitev prostornine stožca uporabite naslednji izraz:

V = 1/3 * S _o * h

Če zamenjamo formulo za S _o , dobimo:

V = 1/3 * pi * r ² * h

Nekateri bralci so morda opazili, da formula za volumen stožca ustreza formuli za piramido. To naključje ni naključno, saj oblike teh številk postanejo identične, če se število robov ravne črte piramide poveča do neskončnosti.