Kaj je stožec v geometriji? Definicija, formule, vzorčni problem

Poznavanje lastnosti geometrijskih številk omogoča ne samo reševanje teoretičnih problemov, temveč tudi izvajanje praktično pomembnih izračunov. Ena takih številk, katerih lastnosti bodo obravnavane v tem članku, je stožec. Kaj je stožec, kakšne vrste so, kako najti njegovo območje in obseg? Vsa ta vprašanja so podrobno predstavljena v nadaljevanju.

Splošna opredelitev stožca v geometriji

Stereometrija, ki proučuje značilnosti številk v tridimenzionalnem prostoru, ponuja naslednji odgovor na vprašanje, kaj je stožec: to je slika, katere površina je sestavljena iz niza ravnih segmentov, ki povezujejo določeno točko v prostoru z določeno krivuljo v ravnini.

Označena točka prostora se imenuje vozlišče stožca, ravni segmenti so generati figure ali njeni generatorji, sama krivulja na ravnini pa je directrix.

V skladu z zgornjo definicijo je primeren celoten razred številk, od katerih so najbolj znani okrogli, eliptični, parabolični in hiperbolični stožci. Eliptična slika je prikazana spodaj.

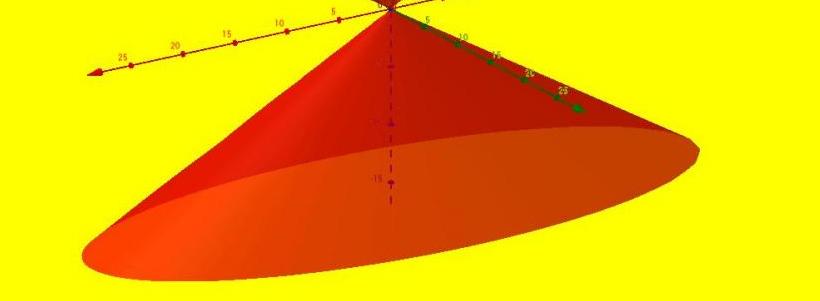
Direktorica tega stožca je zaprta elipsa, ki povezuje osnovo slike. Generacije vseh stožcev skupaj tvorijo stožčasto površino, ki se imenuje stranska. Ti dve površini (osnovna in stranska) omejujeta prostorski volumen, ki se običajno imenuje prostornina stožca.

Okrogel ravni konus - slika vrtenja

Eliptičnega stožca, prikazanega na zgornji sliki, ni mogoče dobiti zaradi vrtenja ravne figure. Edini predstavnik razreda stožcev, ki se lahko oblikujejo z vrtenjem, je okrogel ravni konus. Ta slika je prikazana spodaj.

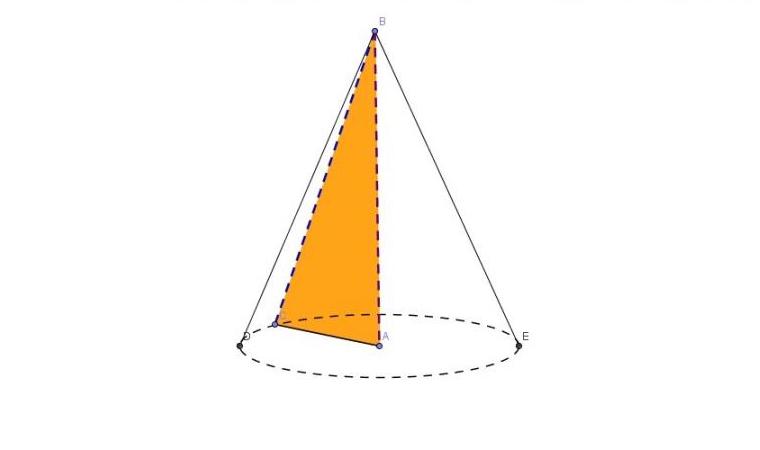
Vidimo lahko, da njegova osnova predstavlja idealen krog. Poleg tega bo vsak odsek stranske ploskve z ravnino, ki je vzporedna z bazo, prav tako krog, vendar z manjšim premerom kot slika na dnu.

Oranžni trikotnik ABC, izbran znotraj stožca, je pravokoten. Vidimo lahko, da je noga AC osnovni polmer r. Noga AB je višina slike h. Po konstrukciji je jasno, da je višina dolžina pravokotnice, ki poteka od vrha slike B do ravnine osnove (kroga). Ta višina seka središče kroga. Slednje pomeni, da je stožec ravna. Nazadnje, hipotenuza trikotnika BC ni nič več kot stožec.

Da bi z opisanim trikotnikom oblikovali stožec, ga je potrebno obrniti okrog strani AB.

Za vizualno predstavitev razlike med ravnimi in poševnimi stožci predstavimo ustrezno sliko.

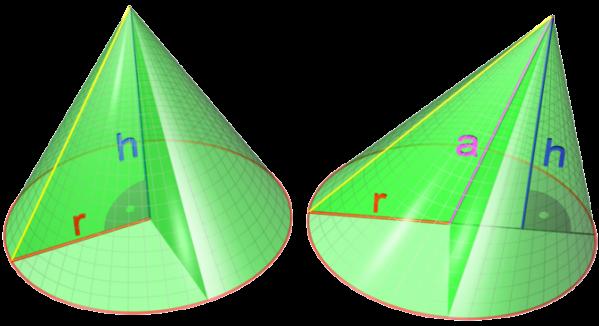
Razlika med dvema številkama je očitna: če so njihove podlage enake, potem se višine znižajo od vrha preko baz na različnih točkah. Prva številka je ravna, druga je poševna.

Linearni parametri okroglega ravnega stožca in kota na dnu

Ti parametri so že navedeni zgoraj. Ponovno jih navedite:

• polmer r;
• višina h;
• generatrix g.

Za enoznačno definiranje stožca so ti trije parametri odvečni, to pomeni, da je mogoče zadevno sliko konstruirati in izračunati vse njene lastnosti, saj vemo samo dva od treh imenovanih parametrov. Na podlagi obravnavane sheme za pridobitev stožca z vrtenjem pravokotnega trikotnika lahko zapišemo naslednjo povezavo med generatorjem, radijem in višino stožca:

g = √ (r² + h²).

Ta enakost je očitna in ne zahteva dokazov (spomnite se Pitagorovega izreka).

Stožec lahko nastavite ne samo s pomočjo ravnih segmentov r, h in g, temveč tudi z uporabo kotnega merila med katerimkoli generatorjem oblike in osnovno ravnino. Ta kot označimo s črko φ. Z definicijo trigonometričnih funkcij lahko zapišemo niz formul, v katerih kot φ povezuje linearne parametre. Pišemo glavne:

g = h / sin (φ);

g = r / cos (φ);

h = r * tg (φ).

Površina slike

Glede na vprašanje, kaj je stožec, predstavimo formulo za določitev območja njene polne površine. Da bi bilo bolj jasno, o čem bomo razpravljali, bomo skeniranje prenesli v ravnino zadevne številke.

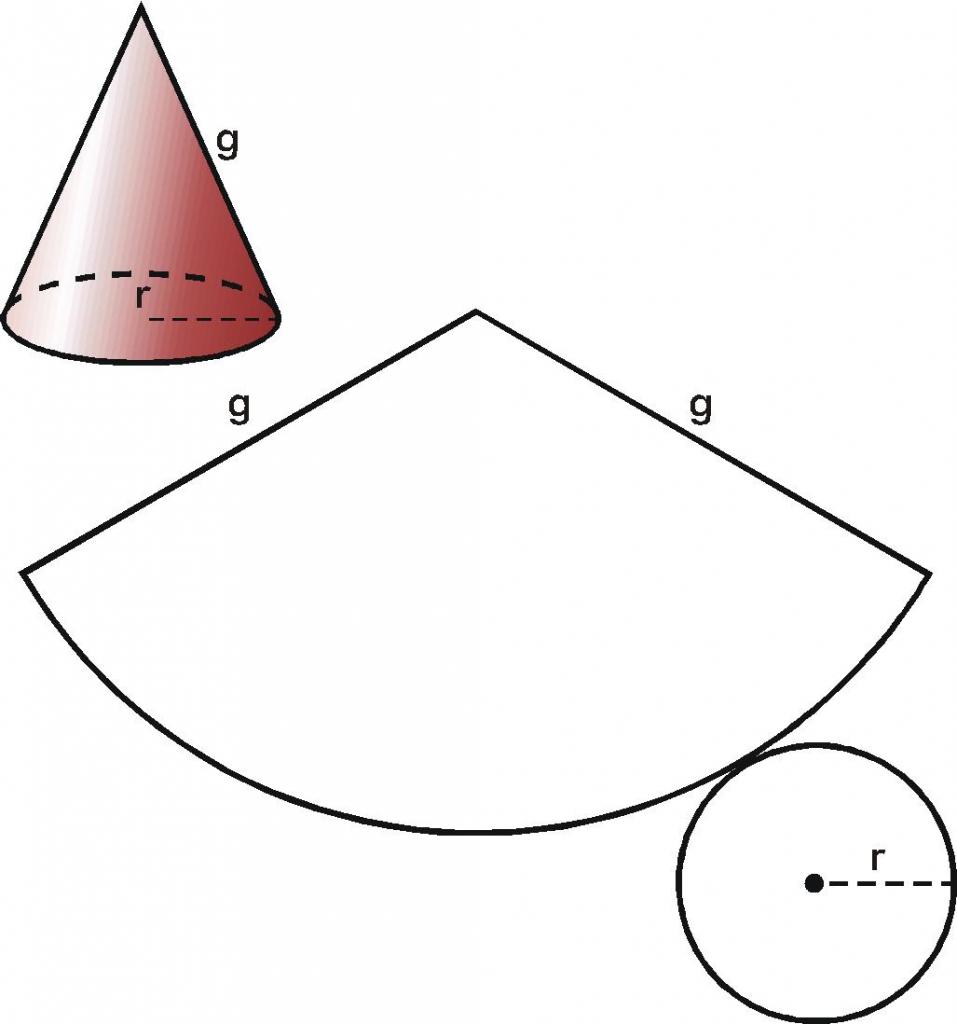
Razvoj stožca na ravnini je sestavljen iz dveh številk. Krog je osnova stožca, krožni del polmera g je bočna površina. Krožni odsek je enostavno pridobiti, če vzamete stožčasto površino papirja in ga razrežete po kateri koli generični g. Če razširimo to površino, dobimo želeni sektor.

Določitev območja S _o kroga ni problem. Ustrezni izraz je prikazan spodaj:

S _o = pi * r².

Za krožni sektor _so znani tudi njeni potrebni parametri za izračun območja S _b : polmer g in dolžina loka, ki ustreza obodu zgornjega kroga. Formula za izračun površine bočne površine stožca S _b je:

S _b = pi * r * g.

Tako je skupna površina številke enaka:

S = S _o + S _b = pi * r * (r + g).

Formula za volumen

Vedeti, kaj je stožec pravokotno, je enostavno napisati formulo za njen volumen. Ker se lahko obravnavana številka šteje za piramido z neskončnim številom stranskih robov, se lahko za to, kot za vsako piramido, izračuna volumen po formuli:

V = 1/3 * S _o * h.

Vrednost kvadrata S _o smo že navedli zgoraj, zato bo zahtevana formula za prostornino ravnega stožca z okroglo osnovo naslednja:

V = 1/3 * pi * r² * h.

Reševanje geometrijskega problema

Znano je, da je vrednost površine stožca okrogle ravne 300 cm². Potrebno je določiti polmer stožca, vedoč, da je njegova generacija 15 cm.

Pišemo enakost za območje in nadomestimo vrednost g = 15 cm in S = 300 cm², dobimo:

S = pi * r * (r + g) =>

300 = pi * r² + 15 * pi * r.

Levo in desno stran delimo s številom pi, dobimo naslednjo kvadratno enačbo:

r² + 15 * r - 95,54 = 0.

Rešimo to enačbo s pomočjo diskriminanta, dobimo:

D = 15² - 4 * (- 95,54) = 607,16;

r = (-15 ± √D) / 2 = (4,82; -19,82).

Negativni koren ne ustreza pogoju problema, tako da lahko napišete odgovor: dani konus ima polmer 4,82 cm.