Kakšne težave čakajo tisti, ki so se zavezali, da bodo izvedli dodajanje korenin?

Tema kvadratnih korenin je obvezna v šolskem učnem načrtu tečaja matematike. Brez njih ne smete storiti, ko se odločate kvadratne enačbe. In kasneje postane potrebno ne samo izvleči korenine, temveč tudi izvajati druge ukrepe z njimi. Med njimi so precej zapleteni: izpostavljenosti množenje in delitev. Vendar pa so precej preproste: odštevanje in dodajanje korenin. Mimogrede, na prvi pogled se zdijo le tako. Če jih brez napak ne vodimo, ni vedno lahko, ko se z njimi začnejo spoznavati.

Kaj je matematični koren?

Ta ukrep je nastal v nasprotju z eksponentiranjem. Matematika predpostavlja obstoj dveh nasprotnih operacij. Za seštevanje je odštevanje. Množenju nasprotuje delitev. Inverzna stopnja je ekstrakcija ustreznega korena.

Če je v moči dva, potem je koren kvadrat. Najpogostejša je v šolski matematiki. Nima niti oznake, da je kvadrat, to pomeni, da mu ni pripisano število 2. Matematična oznaka tega operaterja (radikala) je prikazana na sliki.

Iz opisanega dejanja sledi njegova definicija. Za ekstrakcijo kvadratni koren iz določenega števila morate ugotoviti, katera bo dala, ko se množite vase, radikalni izraz. To število bo kvadratni koren. Če jo matematično zapišete, dobite naslednje: x * x = x ² = y, nato √u = x.

Kaj lahko storite z njimi?

Korenina je v svojem jedru delna stopnja, v kateri je enota v števcu. In imenovalec je lahko vsak. Na primer, pri kvadratnem korenu je enaka dvema. Zato bodo vsa dejanja, ki jih je mogoče izvesti z stopnjami, veljavna za korenine.

In zahteve za te ukrepe so enake. Če množenje, delitev in eksponiranje ne pride do težav za študente, dodajanje korenin, kot je njihovo odštevanje, včasih povzroči zmedo. In vse zato, ker želim opravljati te operacije ne glede na korenski znak. In tu se začnejo napake.

Kakšna so pravila za njihovo dodajanje in odštevanje?

Najprej morate zapomniti dve kategorični "ne":

• ne dodajati in odštevati korenov, kot je številke to pomeni, da ni mogoče napisati enojnih znakov zasedenih radikalnih izrazov in z njimi izvajati matematične operacije;
• ne morete dodajati in odštevati korenin z različnimi kazalniki, kot sta kvadratni in kubični.

Dober primer prve prepovedi: +6 + ≠10 √ √16, vendar √ (6 + 10) = .16 .

V drugem primeru se je bolje omejiti na poenostavitev korenin. In v odgovoru pustite njihov znesek.

Zdaj s pravili

1. Poiščite in združite podobne korenine. To pomeni, da imajo tisti, ki nimajo samo enakih številk pod radikalnim, ampak sami imajo isti kazalnik.
2. Za izvedbo dodajanja korenin, združenih v eno skupino s prvim dejanjem. Preprosto ga je izvajati, saj morate le dodati vrednosti, ki stojijo pred radikalom.
3. Izvlecite korenine v tistih izrazih, v katerih radikalni izraz oblikuje cel kvadrat. Z drugimi besedami, ne pustite ničesar pod znakom radikala.
4. Poenostavite izraz. Če želite to narediti, jih morate razčleniti v prvotne faktorje in preveriti, če ne bodo dali kvadratne številke. Jasno je, da je to res, ko gre za kvadratni koren. Kadar je eksponent tri ali štiri, potem bi morali osnovni faktorji dati kocko ali četrto moč števila.
5. Odstranite od radikalnega množilnika, ki daje celotno stopnjo.
6. Poglejte, če se podobni izrazi ponovno pojavijo. Če je tako, ponovite drugo dejanje.

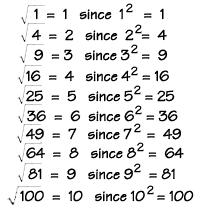
V primeru, ko naloga ne zahteva natančne vrednosti korena, se lahko izračuna na kalkulatorju. Neskončni decimalni del, ki bo prikazan v oknu okna. Najpogosteje je to storjeno do stotine. In nato opravite vse operacije za decimalne frakcije.

Priporočilo: po razgradnji v osnovne faktorje morate preveriti. To pomeni, da jih pomnožite drug na drugega in preverite, ali je prvotna vrednost pridobljena.

To so vse informacije o tem, kako se izvaja dodajanje korenin. Spodnji primeri ponazarjajo zgoraj navedeno.

Prva naloga

Izračunajte vrednost izrazov:

a) +2 + 3√32 + ½ 8128 - 6√18;

b) --75 - 7147 + --48 - 1/5 ;300;

c) --275 - 10√11 + 2√99 + 6396.

Odločitev.

a) Če sledite zgornjemu algoritmu, je jasno, da za prva dva dejanja v tem primeru ni ničesar. Lahko pa poenostavite nekatere radikalne izraze.

Na primer, 32 se razgradi na dva faktorja 2 in 16; 18 je enak produktu 9 in 2; 128 je 2 s 64. Glede na to bo izraz napisan takole:

+2 + 3√ (2 * 16) + ½ 2 (2 * 64) - 6 √ (2 * 9).

Zdaj moramo odstraniti iz radikalnega znaka tiste dejavnike, ki dajejo kvadrat števila. To je 16 = 4 ² , 9 = 3 ² , 64 = 8 ² . Izraz bo izgledal tako:

+2 + 3 * 4√2 + ½ * 8 --2 - 6 * 3√2.

Potrebujete malo lažje pisati. V ta namen pomnožite koeficiente pred znaki korena:

+2 + 12√2 + 4 --2 - 12√2.

V tem izrazu so se vsi izrazi izkazali za podobne. Zato morajo samo zložiti. Odgovor bo: 5√2.

b) Kot v prejšnjem primeru se dodatek korenin začne z njihovo poenostavitvijo. Radikalni izrazi 75, 147, 48 in 300 bodo predstavljeni z naslednjimi pari: 5 in 25, 3 in 49, 3 in 16, 3 in 100. Vsak od njih ima številko, ki jo je mogoče odstraniti iz korenskega znaka:

5√5 - 7√3 + 4√3 - 1/5 * 10√3.

Po poenostavitvi dobimo odgovor: 5√5 - 5√3. Lahko se pusti v tej obliki, vendar je bolje vzeti skupni faktor 5 za oklepaje: 5 (--5 - )3).

c) In spet, faktoring: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. Po odstranitvi faktorjev iz korenskega znaka dobimo:

5√11 - 10√11 + 2 * 3√11 + 6√11. Po takšnih pogojih dobimo rezultat: 7√11.

Primer z delnimi izrazi

√ (45/4) - --20 - 5√ (1/18) - 1/6 45245 + √ (49/2).

Dejavniki bodo morali razčleniti naslednje številke: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Podobno kot že obravnavani, morate odstraniti dejavnike iz znaka korena in poenostaviti izraz:

3/2 --5 - 2√5 - 5/3 √ (½) - 7/6 +5 + 7 (½) = (3/2 - 2 - 7/6) --5 - (5/3 - 7 ) √ (½) = - 5/3 +5 + 16/3 √ (½).

Ta izraz zahteva, da se znebimo iracionalnosti v imenovalcu. Da bi to naredili, pomnožimo z /2 / √2 drugi izraz:

- 5/3 +5 + 16/3 √ (½) * /2 / =2 = - 5/3 +5 + 8/3 .2.

Za popolnost dejanja je potrebno pred koreni izbrati celo število dejavnikov. V prvem je enak 1, v drugem - 2.