Kaj so čudne številke in kako jih spoznati?

Preden govorimo o parnih in lihih številkah, je smiselno pojasniti nekaj točk o tem, katere skupine številk so na splošno. To je potrebno, da ne bi poskušali ugotoviti paritete frakcije.

Kakšne so številke za začetek šolanja v osnovni šoli?

Prvi so naravni. Prvič so se pojavili tudi zgodovinsko. Človeštvo je moralo šteti predmete. Poleg tega se pri štetju nič ne uporablja, zato ni vključena v skupino naravnih števil. Tu so vse številke, ki so večje od enega.

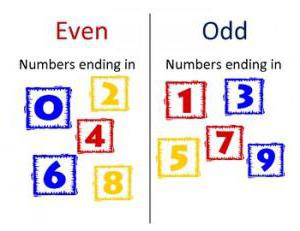
Za njih je prva definicija paritete. Da bi razumeli, kakšno število je čudno, se morate spomniti znaka parne. Konča se z eno od številk: 0, 2, 4, 6, 8. Vsi ostali bodo lihi. Najmanj njih je ena. Maksimum ne obstaja.

Katere številke se nadaljujejo?

Cela. Njihova množica že vključuje ničelna in vsa negativna števila. Veriga naravnih števil je bila omejena levo, desno pa se je nadaljevala v nedogled. Z celimi številkami se izkaže, da je neskončno število števil in levo od nič.

Na tej točki se definicija paritete nekoliko spremeni. Zdaj jo je treba razdeliti na dva dela brez preostanka. Zato nenavadna števila, ki jih delimo z dvema, dajo odgovor s preostankom.

Vnese se celo splošni zapis: za celo - 2n, liho - (2n + 1). Če za naravno ni samo največje parne ali liho, potem cela števila nimajo minimuma.

In kaj potem?

Racionalne številke (drugo ime - resnično). Poleg že omenjenih, ta sklop vključuje tudi dele. To je število, ki ga lahko predstavimo kot dve. Prvi je števec in je predstavljen kot celo število. Drugi je imenovalec, ki ni nikoli nič.

Mimogrede, koncept paritete za njih ni uveden. Zato liha števila, zapisana kot frakcija, sploh ne obstajajo.

Kakšne rezultate dajejo akcije s parnimi in lihimi številkami?

Lahko jih obravnavamo v skladu z naraščajočo kompleksnostjo aritmetične operacije. Potem bosta prvi in ​​drugi dodatek in odštevanje. Ne glede na to, kateri se izvede, bo odgovor odvisen samo od začetnega para številk. Na primer, če so začetne številke parne, se bo rezultat akcije delil z dvema. Enak rezultat bo, če obstaja razlika ali vsota lihih števil. Če želite dobiti liho število, morate dodati ali odštevati celo z lihim številom.

To je mogoče preprosto preveriti z njihovim splošnim zapisom. Na primer, dodajanje dveh sodih števil: 2n + 2n = 4n = 2 * 2n. Tu je 2n celo število, ki je še vedno pomnoženo z dvema. Torej bo vsekakor popolnoma razdeljena v dvojico. Odgovor je enak.

Pri dodajanju celo v liho imamo naslednji vnos: 2n + (2n + 1) = 4n + 1. Prvi izraz je sodo število, ki mu je dodano. Zadnji izraz ne bo omogočil, da se ta rezultat v celoti razdeli na dva.

Tretji ukrep je množenje. Ko se izvede, bo vedno odgovoren, če je vsaj en enak faktor. V primeru, ko se dva liha števila pomnožita skupaj, bo rezultat lih.

Za ponazoritev slednjega morate narediti naslednji vnos: (2n + 1) * (2n + 1) = 4n + 2n + 2n + 1 = 8n + 1. Ponovno je prvi izraz celo število in enota bo naredila liho.

S četrtim dejanjem - delitvijo - vse ni tako jasno. Lahko začnete z dvema enakima. Prvič, delček se lahko izkaže, potem pariteta ni vprašanje. Drugič, rezultat je celo število. Toda tudi takrat dokončnega odgovora na vprašanje prihodnje paritete ne moremo dobiti. Lahko jo ocenite šele po delitvi. Odgovor je lahko enak in nenavaden.

Če je liho število deljeno s sodo številko, je odgovor vedno deljen. Njena pariteta torej ni določena.

Kadar so v delitvi vključeni lihi številki, je lahko rezultat tudi ulomek. Toda če je odgovor celovit, bo zagotovo čudno.

Pri deljenju celo na liho, kot v prejšnji situaciji, obstajata dve možnosti: frakcija ali celo število. V drugem primeru bo vedno enakomerno.