Vrste trikotnikov. Trikotni koti

Najenostavnejši poligon, ki ga preučujemo v šoli, je trikotnik. Je bolj razumljiva za študente in se srečuje z manj težavami. Kljub temu, da obstajajo različne vrste trikotnikov, ki imajo posebne lastnosti.

Kakšno obliko imenujemo trikotnik?

Oblikovan s tremi točkami in segmenti. Prvi se imenujejo vertices, druga stran. Poleg tega morajo biti vsi trije segmenti med seboj povezani v kote. Zato je ime "trikotnik".

Razlike v imenih vogalov

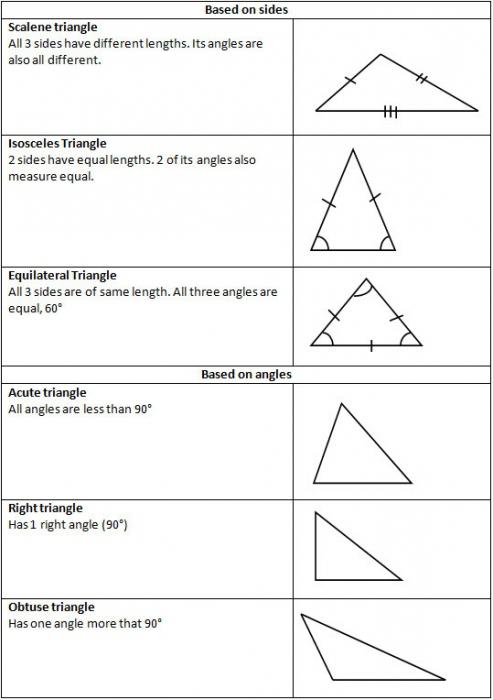
Ker so lahko ostra, topa in ravna, so ti trikotniki določeni s temi imeni. Obstajajo tri skupine takih številk.

• Prvi. Če so vsi vogali trikotnika akutni, bo imelo ime akutnega kota. Vse je logično.

• Drugi. Eden od vogalov je nejasen, kar pomeni trikotni vogal. Tam preprosto ni prostora.

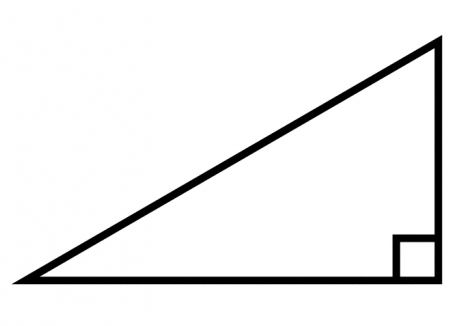
• Tretjič. Obstaja kot 90 stopinj, ki se imenuje naravnost. Trikotnik postane pravokoten.

Razlike v imenih na straneh

Ti tipi trikotnikov se razlikujejo glede na značilnosti stranic:

• splošni primer je vsestranski, kjer imajo vse strani poljubno dolžino;

• enakokračni, katerih obe strani imata enake številčne vrednosti;

• enakovredni, so dolžine vseh njegovih strani enake.

Če naloga ne določa posebne vrste trikotnika, potem morate narisati poljubno. V katerih so vsi koti ostri, in stranice imajo različne dolžine.

Lastnosti, skupne vsem trikotnikom

1. Če dodate vse vogale trikotnika, dobite številko, ki je enaka 180º. In ne glede na to, kako izgleda. To pravilo je vedno veljavno.
2. Številčna vrednost obeh strani trikotnika je manjša od preostalih dveh. Hkrati pa je več kot njihova razlika.
3. Vsak zunanji vogal ima vrednost, ki jo dobimo z dodajanjem dveh notranjih, ne sosednjih. Poleg tega je vedno večja od notranjega, ki leži ob njem.
4. Nasproti manjše strani trikotnika je vedno najmanjši kot. Nasprotno, če je stran velika, bo kot največji.

Te lastnosti so vedno veljavne, ne glede na to, kateri trikotniki so obravnavani v problemih. Vsi ostali sledijo posebnim značilnostim.

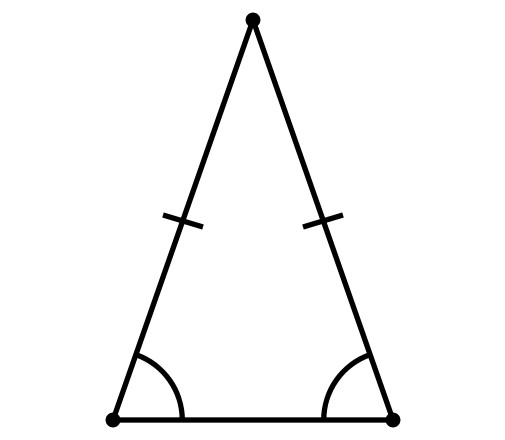
Lastnosti enakokrakega trikotnika

• Koti, ki ležijo ob dnu, so enaki.
• Višina, ki se drži do baze, je tudi mediana in simetrala.
• Višine, mediane in bisektorji, ki so zgrajeni na straneh trikotnika, so med seboj enaki.

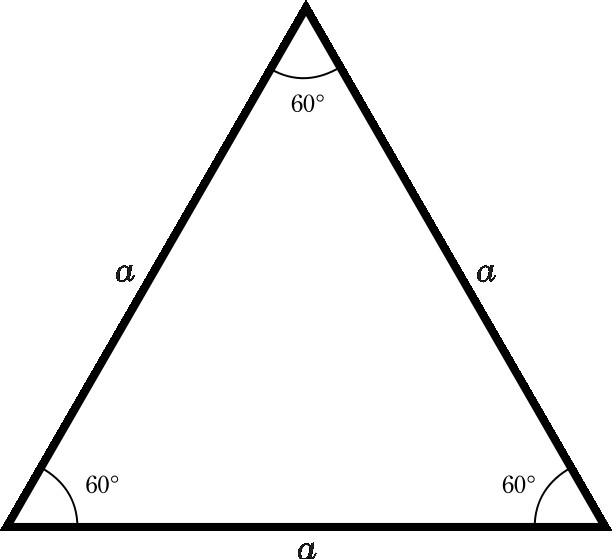
Lastnosti enakostraničnega trikotnika

Če obstaja takšna številka, bodo vse zgoraj opisane lastnosti resnične. Ker bo enakostranični vedno enakokračni. Vendar ne obratno, enakokraki trikotnik ne bo nujno enakostranični.

• Vsi njegovi koti so med seboj enaki in imajo vrednost 60 °.
• Vsaka srednja vrednost enakostraničnega trikotnika je njegova višina in simetrala. Vsi so enaki. Za določitev njihovih vrednosti obstaja formula, ki je sestavljena iz produkta stranke kvadratni koren od 3 deljeno z 2.

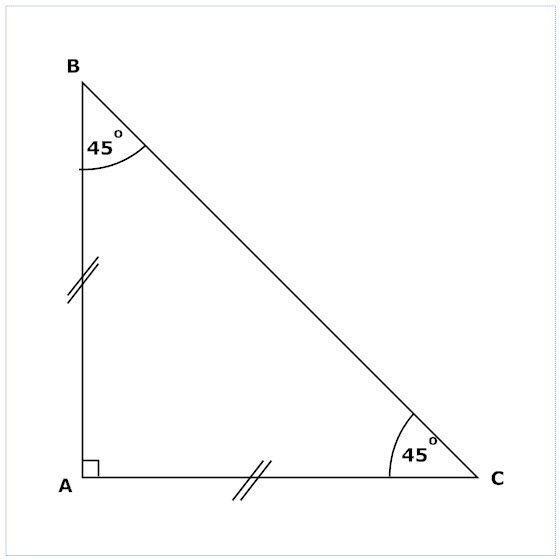
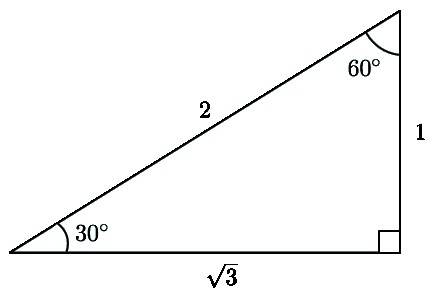
Lastnosti pravokotnega trikotnika

• Dva ostra kota podajata skupno vrednost 90 °.
• Dolžina hipotenuze je vedno večja od dolžine katerekoli noge.
• Številčna vrednost mediane, opravljene za hipotenuzo, je polovica.
• Ista vrednost je enaka nogi, če leži nasproti kota 30 °.
• Višina, ki je narisana z vrha z vrednostjo 90 °, ima določeno matematično odvisnost od nog: 1 / n ² = 1 / a ² + 1 / in ² . Tukaj: a, c - noge, n - višina.

Naloge z različnimi tipi trikotnikov

№1. Podan je enakokračni trikotnik. Območje je znano in znaša 90 cm in mora poznati njegove strani. Kot dodatni pogoj: stran je manj kot osnova za 1,2-krat.

Rešitev

Vrednost območja je neposredno odvisna od vrednosti, ki jih je treba najti. Vsota vseh treh strani bo dala 90 cm, zdaj pa se moramo spomniti znaka trikotnika, v katerem je enakokraka. To pomeni, da sta obe strani enaki. Lahko naredimo enačbo z dvema neznankama: 2a + b = 90. Tu je a stran, v - baza.

To je obrat dodatnega pogoja. Po njem dobimo drugo enačbo: v = 1,2a. Ta izraz lahko nadomestite v prvem. Izkazalo se je: 2a + 1.2a = 90. Po transformacijah: 3.2a = 90. Od tu je = 28.125 (cm). Zdaj je enostavno ugotoviti podlago. To je najbolje iz drugega pogoja: c = 1,2 * 28,125 = 33,75 (cm).

Če želite preveriti, lahko dodate tri vrednosti: 28.125 * 2 + 33.75 = 90 (cm). Tako je.

Odgovor: stranice trikotnika so 28,125 cm, 28,125 cm, 33,75 cm.

№2. Stran enakostraničnega trikotnika je 12 cm, njegova višina pa je treba izračunati.

Odločitev. Za iskanje odgovora je dovolj, da se vrnemo na točko, kjer smo opisali lastnosti trikotnika. To je formula za iskanje višine, mediane in simetrala enakostraničnega trikotnika.

n = a * /3 / 2, kjer je n višina in a stran.

Zamenjava in izračun dajejo naslednji rezultat: n = 6 × 3 (cm).

Te formule ni treba zapomniti. Naj spomnimo, da višina deli trikotnik na dva pravokotna. Poleg tega se izkaže, da je noga, in hipotenuza v njej je stran originala, druga noga je polovica znane strani. Sedaj morate napisati Pitagorejski izrek in izpeljati formulo za višino.

Odgovor: višina je 6 cm 3 cm.

№3. Podan je MKR - trikotnik, 90 stopinj, pri katerem je kot K. Izdelki MR in KR znani, so enaki 30 in 15 cm, zato je treba ugotoviti vrednost kota R.

Odločitev. Če naredite risbo, postane jasno, da je MR hipotenuza. In to je dvakrat več kot KR. Spet se morate sklicevati na lastnosti. Ena od njih je povezana z vogali. Iz nje je jasno, da je kot CMR enak 30 °. Želeni kot P je enak 60 °. To izhaja iz druge lastnosti, ki navaja, da mora biti vsota dveh akutnih kotov 90 °.

Odgovor: P kot je 60 °.

№4. Morate najti vse kote enakokrakega trikotnika. O njem je znano, da je zunanji kot od kota pri podstavku 110 °.

Odločitev. Ker je podan le zunanji vogal, ga je treba uporabiti. Oblikuje se z notranjim kota raztegnjena. Tako bodo skupaj dobili 180º. To pomeni, da bo kot na dnu trikotnika enak 70 °. Ker je enakokrako, ima drugi kot enak pomen. Še vedno je treba izračunati tretji kot. Z lastnostjo, ki je skupna vsem trikotnikom, je vsota kotov 180º. Tretji je torej opredeljen kot 180º - 70º - 70º = 40º.

Odgovor: koti so 70º, 70º, 40º.

№5. Znano je, da je v enakokrakovem trikotniku kot, ki leži nasproti dnu, 90 °. Na podlagi označene točke. Segment, ki ga povezuje s pravim kotom, ga deli v razmerju 1 do 4. Vedeti morate vse kote manjšega trikotnika.

Odločitev. Eden od vogalov je mogoče takoj prepoznati. Od takrat pravokotni trikotnik in enakokračni, potem bodo tisti, ki ležijo v njeni bazi, na 45 °, to je pri 90 ° / 2.

Drugi od njih bo pomagal najti znano razmerje med pogoji. Ker je enaka 1 do 4, dobimo deleže, ki se delijo, samo 5. Zato, da bi ugotovili manjši kot trikotnika, potrebujemo 90º / 5 = 18º. Še vedno se moramo naučiti tretjega. V ta namen od 180º (vsota vseh kotov trikotnika) odštejemo 45º in 18º. Izračuni so preprosti in izkaže se: 117º.

Odgovor: 18º, 45º, 117º