Projekcija točke na ravnini. Projekcija točke na ravni črti na ravnini
Proučevanje lastnosti številk v prostoru in na ravnini je nemogoče brez poznavanja razdalj med točko in takšnimi geometrijskimi objekti kot ravna črta in ravnina. V tem članku bomo pokazali, kako najti te razdalje, upoštevajoč projekcijo točke na ravnini in na ravni črti.
Enačba črte za dvodimenzionalne in tridimenzionalne prostore
Izračun razdalje točke do ravne črte in ravnine se izvede z njegovo projekcijo na te objekte. Da bi lahko našli te projekcije, moramo vedeti, v kakšni obliki so podane enačbe za ravne črte in ravnine. Začnimo s prvim.
Ravna črta je zbirka točk, od katerih je vsaka pridobljena iz prejšnjega s prenosom v vzporedne vektorje. Na primer, obstaja točka M in N. Vektor MN connecting, ki ju povezuje, vzame M do N. Tudi tretja točka P. Če je vektor MP¯ ali NP¯ vzporeden z MN¯, potem vse tri točke na eni liniji ležijo in ga tvorijo.
Odvisno od dimenzije prostora lahko enačba, ki določa linijo, spremeni svojo obliko. Dobro znana linearna odvisnost koordinate y od x v prostoru opisuje ravnino, ki je vzporedna s tretjo osjo z. V zvezi s tem bomo v tem članku obravnavali le vektorsko enačbo za linijo. Ima enak videz za ravnino in tridimenzionalni prostor.
V presledku je ravna črta lahko definirana z naslednjim izrazom:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (a; b; c)
Tukaj koordinatne vrednosti z ničelnimi indeksi ustrezajo premici, ki pripada določeni točki, u¯ (a; b; c) je koordinata usmerjevalnega vektorja, ki leži na dani premici, α je poljubno realno število, ki lahko spremeni vse točke ravnine. Ta enačba se imenuje vektor.
Pogosto je zgornja enačba napisana v odprti obliki:
x = x 0 + a * a;
y = y 0 + α * b;
z = z 0 + α * c
Podobno lahko zapišemo enačbo za ravno črto v ravnini, to je v dvodimenzionalnem prostoru:
(x; y) = (x 0 ; y 0 ) + α * (a; b);
x = x 0 + a * a;
y = y 0 + α * b
Ravninska enačba
Da bi lahko našli razdaljo od točke do ravnin projekcij, morate vedeti, kako je ravnina definirana. Poleg ravne črte je lahko predstavljena na več načinov. Pri tem upoštevamo samo eno: splošno enačbo.
Recimo, da točka M (x 0 ; y 0 ; z 0 ) pripada ravnini, vektor n ¯ (A; B; C) pa je pravokoten na to, nato pa za vse točke (x; y; z) ravnine velja naslednja enakost:
A * x + B * y + C * z + D = 0, kjer je D = -1 * (A * x 0 + B * y 0 + C * z 0 )
Ne smemo pozabiti, da so v tej splošni enačbi ravnine koeficienti A, B in C koordinate normale na ravnino vektorja.
Izračun razdalje s koordinatami
Preden nadaljujemo z upoštevanjem projekcij na ravnini točke in na ravni črti, je treba opozoriti, kako je treba izračunati razdaljo med dvema znanim točkam.
Recimo, da obstajata dve prostorski točki:
A 1 (x 1 ; y 1 ; z 1 ) in A 2 (x 2 ; y 2 ; z 2 )
Potem se razdalja med njimi izračuna po formuli:
A 1 A 2 = √ (((x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 + (z 2 -z 1 ) 2 )
S tem izrazom je določena tudi dolžina vektorja A 1 A 2 ¯.
Za primer na ravnini, ko sta dve točki podani s parom koordinat, lahko napišemo podobno enačbo brez prisotnosti člana z z v njem:
A 1 A 2 = √ (((x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 )
Sedaj bomo obravnavali različne primere projekcije na ravnini točke na ravni črti in na ravnini v prostoru.
Točka, črta in razdalja med njimi
Recimo, da obstaja točka in ravna črta:
P 2 (x 1 ; y 1 );
(x; y) = (x 0 ; y 0 ) + α * (a; b)
Razdalja med temi geometrijskimi objekti bo ustrezala dolžini vektorja, katerega začetek leži v točki P 2 , konec pa je na takšni točki P na označeni premici, za katero je vektor P 2 P ¯ te premice pravokoten. Točka P se imenuje projekcija točke P 2 na zadevno linijo.
Spodnja slika prikazuje točko P 2 , njeno razdaljo d na premico in tudi vektor smeri v 1 ¯. Tudi na progi izberemo poljubno točko P 1 in iz nje potegnemo vektor do P 2 . Točka P tukaj sovpada s krajem, kjer pravokotnica prečka črto.
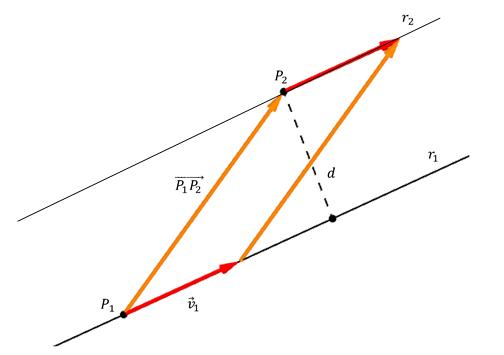
Vidimo, da oranžna in rdeča puščica tvorita paralelogram, katerega strani sta vektor P 1 P 2 ¯ in v 1 ¯, višina pa d. Iz geometrije je znano, da je treba, da bi našli višino paralelograma, njeno območje deliti z dolžino podnožja, na katerem je navpičnica spuščena. Ker je območje paralelograma izračunano kot vektorski produkt njegovih strani, dobimo formulo za izračun d:
d = | [P 1 P 2 ¯ * v 1 ¯] | / | v 1 ¯ |
Vsi vektorji in koordinate točk v tem izrazu so znani, zato jih lahko uporabite brez kakršnih koli transformacij.
Težavo bi lahko rešili drugače. V ta namen zapišite dve enačbi:
- skalarni produkt P 2 P ¯ na v 1 ¯ mora biti enak nič, ker so ti vektorji medsebojno pravokotni;
- koordinate točke P morajo izpolnjevati enačbo črte.
Te enačbe so dovolj, da najdemo koordinate P, nato pa dolžino d po formuli iz prejšnjega odstavka.
Naloga iskanja razdalje med črto in točko
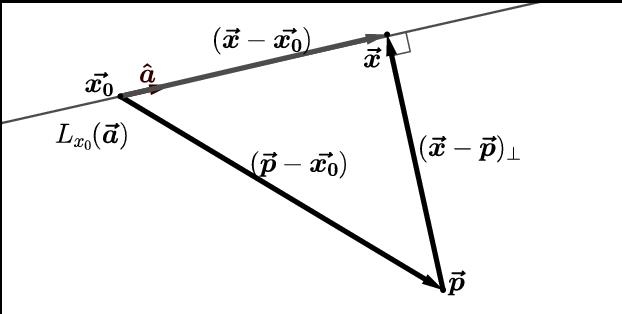
Pokazali bomo, kako te teoretične informacije uporabiti za reševanje specifičnega problema. Recimo, da sta znana naslednja točka in vrstica:
M (5, -3);
(x; y) = (3; 1) - α * (0; 2)
Potrebno je najti točke projekcije na ravni črti na ravnini in razdaljo od M do ravne črte.
Označimo projekcijo, ki jo najdemo s točko M 1 (x 1 ; y 1 ). Ta problem rešujemo na dva načina, opisana v prejšnjem odstavku.
Metoda 1. Smerni vektor v 1 ¯ ima koordinate (0; 2). Če želite zgraditi paralelogram, izberite točko, ki pripada ravni črti. Na primer, točka s koordinatami (3; 1). Nato bo vektor druge strani paralelograma imel koordinate:
(5; -3) - (3; 1) = (2; -4)
Zdaj je treba izračunati produkt vektorjev, ki določajo stranice vzporednika:
[(2; -4) * (0; 2)] = 4
To vrednost nadomestimo s formulo, dobimo razdaljo d od M do ravne črte:
d = 4 / =4 = 2
Metoda 2. Zdaj bomo na drug način našli ne samo razdaljo, ampak tudi koordinate projekcije M na progi, kot to zahteva stanje problema. Kot je navedeno zgoraj, je za rešitev problema potrebno ustvariti sistem enačb. Izgledala bo:
(x 1 -5) * 0 + (y 1 +3) * 2 = 0;
(x 1 ; y 1 ) = (3; 1) -α * (0; 2)
Rešimo ta sistem:
y 1 = -3;
x 1 = 3
Projekcija izhodiščne točke koordinate je M 1 (3; -3). Potem je zahtevana razdalja:
d = | MM 1 ¯ | = √ (4 + 0) = 2
Kot lahko vidite, sta obe rešitvi dali enak rezultat, kar kaže na pravilnost izvedenih matematičnih operacij.
Projekcija točke na ravnini
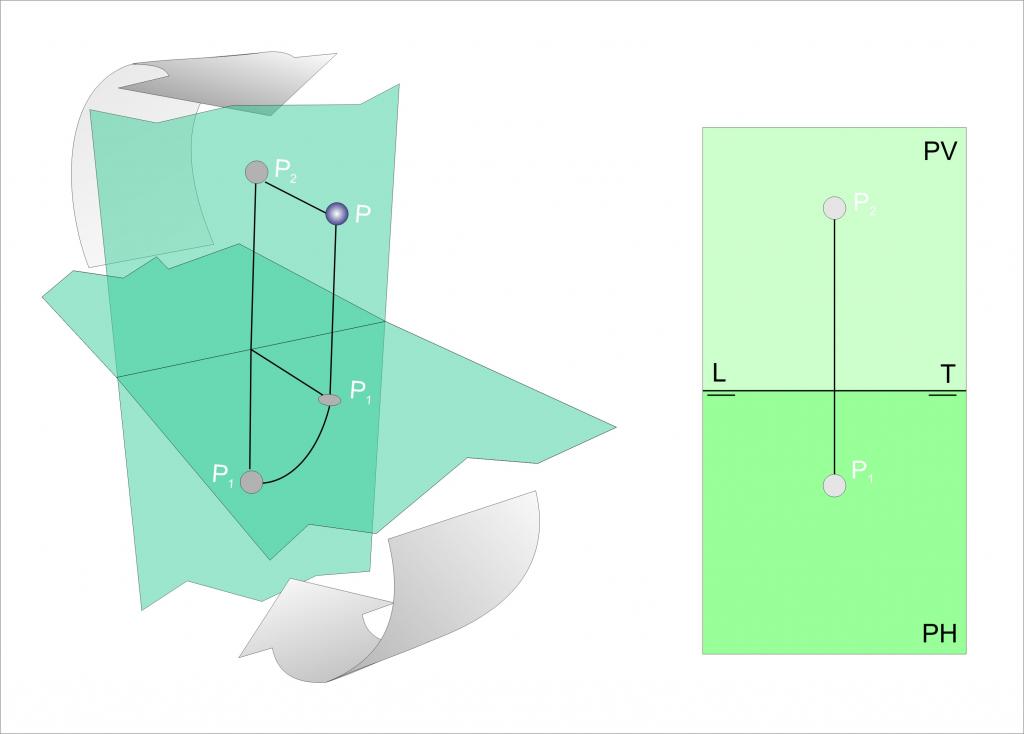
Zdaj razmislite, kaj je projekcija točke, podane v prostoru na določeni ravnini. Ni težko uganiti, da je ta projekcija tudi točka, ki skupaj z izvirno oblikuje vektor, ki je pravokoten na ravnino.
Predpostavimo, da ima projekcija na ravnini koordinat M točke naslednje:
M 1 (x 1 ; y 1 ; z 1 )
Sama ravnina je opisana z enačbo:
A * x + B * y + C * z + D = 0
Na podlagi teh podatkov lahko naredimo enačbo premice, ki prečka ravnino pod pravim kotom in poteka skozi M in M 1 :
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (A; B; C)
Tukaj so spremenljivke z ničelnimi indeksi koordinate točke M. Možno je izračunati položaj na ravnini točke M 1 ob predpostavki, da morajo njene koordinate izpolnjevati obe zapisani enačbi. Če te enačbe ne zadostujejo za reševanje problema, lahko uporabimo pogoj vzporednosti MM 1 ¯ in smerni vektor za dano ravnino.
Očitno je, da projekcija točke, ki pripada ravnini, sovpada z njo, in ustrezna razdalja je nič.
Naloga s točko in ravnino
Pustiti določeno točko M (1; -1; 3) in ravnino, ki je opisana z naslednjo splošno enačbo:
-x + 3 * y -2 * z + 4 = 0
Potrebno je izračunati koordinate projekcije na ravnini točke in izračunati razdaljo med temi geometrijskimi objekti.
Za začetek konstruiramo enačbo črte, ki poteka skozi M in pravokotno na prikazano ravnino. Izgleda:
(x; y; z) = (1; -1; 3) + α * (- 1; 3; -2)
Označimo točko, kjer ta premica seka ravnino, M 1 . Enakost za ravnino in ravno črto mora biti izpolnjena, če v njih nadomestimo koordinate M 1 . Če izrecno zapišemo enačbo ravne črte, dobimo naslednje štiri enačbe:
-x 1 + 3 * y 1 -2 * z 1 + 4 = 0;
x 1 = 1 - α;
y 1 = -1 + 3 * α;
z 1 = 3 - 2 * α
Iz zadnje enakosti dobimo parameter α, nato ga nadomestimo v predzadnjem in drugem izrazu, dobimo:
a = (3-z 1 ) / 2;
y1 = -1 + 3 * (3-z 1 ) / 2 = -3 / 2 * z 1 + 3.5;
x 1 = 1 - (3-z 1 ) / 2 = 1/2 * z 1 - 1/2
Izraz za y 1 in x 1 se nadomesti v enačbo za ravnino, imamo:
-1 * (1/2 * z 1 - 1/2) + 3 * (- 3/2 * z 1 + 3.5) -2 * z 1 + 4 = 0
Kje dobimo:
z 1 = 15/7
Nato:
y 1 = -3 / 2 * 15/7 + 3.5 = 2/7;
x 1 = 1/2 * 15/7 - 1/2 = 4/7
Ugotovili smo, da projekcija točke M na dano ravnino ustreza koordinatam (4/7; 2/7; 15/7).
Zdaj izračunajte razdaljo | MM 1 ¯ |. Koordinate ustreznega vektorja so:
MM 1 ¯ (-3/7; 9/7; -6/7)
Zahtevana razdalja je:
d = | MM 1 ¯ | = /126 / 7 ≈ 1.6
Tri točke projekcije
Med izdelavo risb je pogosto potrebno pridobiti projekcije odsekov na medsebojno pravokotnih treh ravninah. Zato je koristno razmisliti, kakšne so projekcije določene točke M s koordinatami (x 0 ; y 0 ; z 0 ) na tri koordinatne ravnine.

Ni težko pokazati, da je ravnina xy opisana z enačbo z = 0, ravnina xz ustreza izrazu y = 0, preostala ravnina yz pa je označena z enakostjo x = 0.
za x = 0: (0; y 0 ; z 0 );
za y = 0: (x 0 ; 0; z 0 );
za z = 0: (x 0 ; y 0 ; 0)
Kje je pomembno poznati projekcije točke in njene razdalje do ravnin?
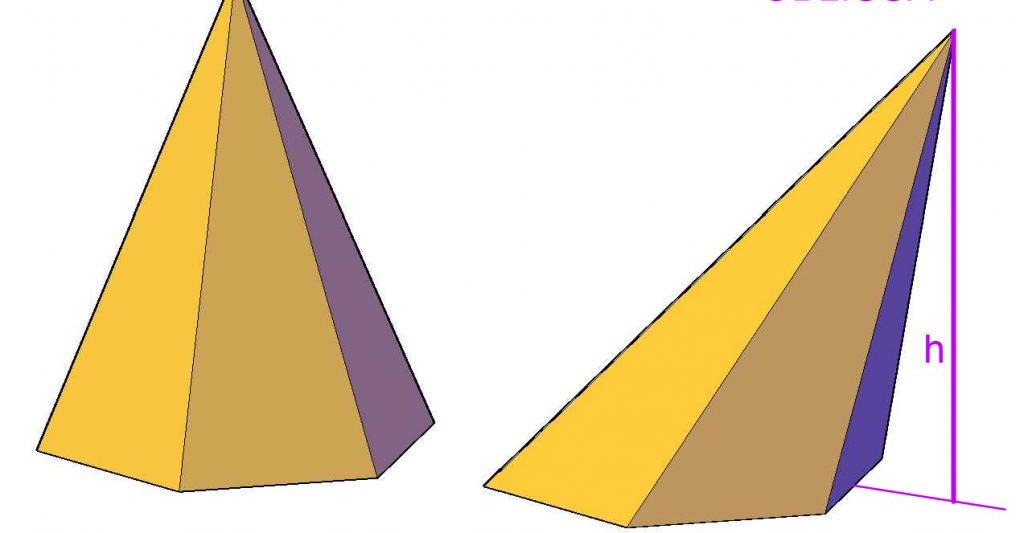
Določanje položaja projekcije točk na določeni ravnini je pomembno pri iskanju takšnih količin, kot so površina in prostornina za poševne prizme in piramide. Razdalja od vrha piramide do ravnine osnove je na primer višina. Slednje je vključeno v formulo za obseg te številke.
Obravnavane formule in metode za določanje projekcij in razdalj od točke do ravne črte in ravnine so dokaj enostavne. Pomembno je le, da si zapomnimo ustrezne oblike ravninskih in neposrednih enačb ter da imamo dobro prostorsko domišljijo, da jih lahko uspešno uporabimo.