Pojav refrakcije. Koti loma in padca. Navidezna globina rezervoarja

Pojav refrakcije je vizualni učinek, ki se pojavi, ko svetlobni žarek prečka vmesnik med dvema medijema, ki sta zanj pregledna. Pomembne značilnosti tega učinka so lomni količniki in koti vpadnosti in lomov. V tem članku obravnavamo bolj podrobno ta optični fenomen.

Snellov zakon za fenomen refrakcije

Kot veste, se vsak val, vključno z elektromagnetnim, širi v ravni liniji in pri konstantni hitrosti v homogenem materialu. Takoj, ko pride do kršitev homogenosti tega materiala, val spremeni svojo pravokotno pot. Živ primer takšne spremembe je lom svetlobe.

Refrakcija žarka se pojavi na lokalizirani točki v prostoru, ki se nahaja na vmesniku dveh transparentnih medijev z različnimi fizikalnimi lastnostmi. Na primer, ta okolja so lahko steklo, zrak, voda, prozorna plastika in drugi. Ko zadane drugi medij, svetloba odstopa za določen kot od prvotne poti.

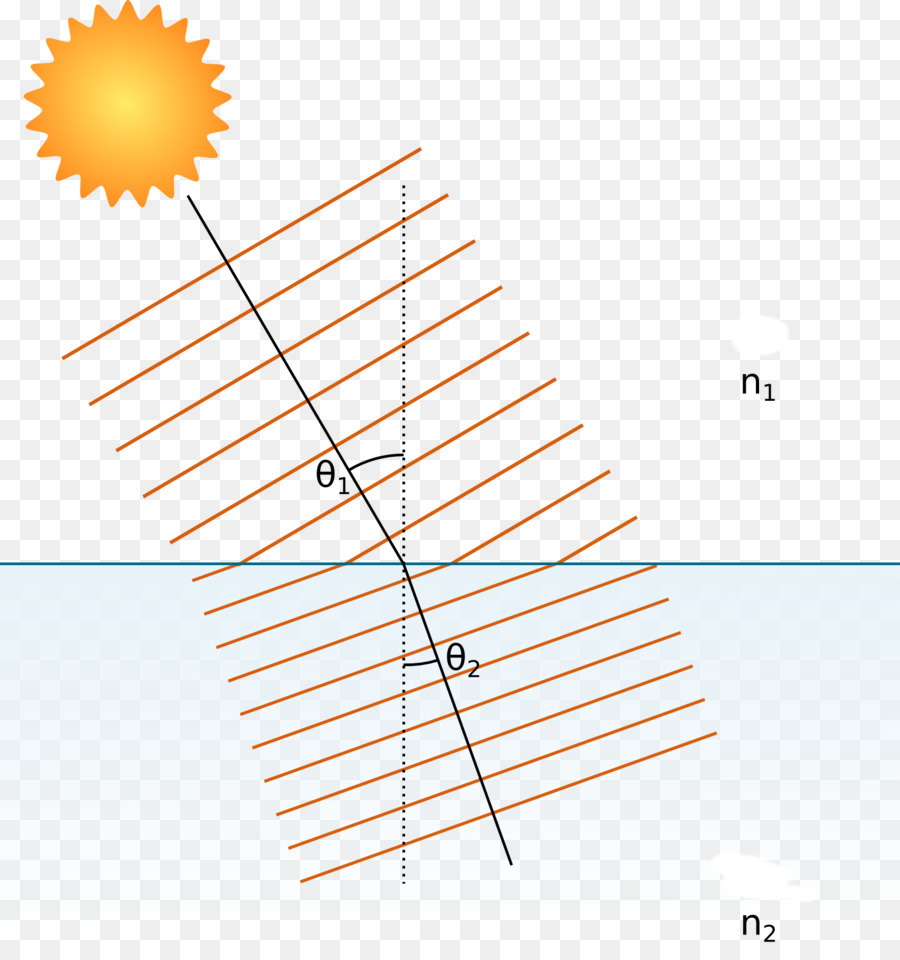
Če mentalno narišete pravokotnico skozi točko, kjer žarek seka ravnino ločevanja medijev in določite kot med pravokotnico in žarkom kot θ ₁ in kot med pravokotnico in žarkom, ki je prešel v drugi medij, kot θ ₂ , potem velja naslednje razmerje:

sin (θ ₁ ) * n ₁ = sin (θ ₂ ) * n ₂

Koti theta-enega (θ ₁ ) in theta-dva (θ ₂ ) se imenujejo koti vpadnosti oziroma lom. Vrednosti n ₁ , n ₂ so pomembne optične lastnosti prvega in drugega medija, imenujemo jih refrakcijski indeksi.

Navedeno formulo imenujemo zakon Snell (Snellius), ker ga je nizozemski znanstvenik Willebrord Snellus na začetku XVII. Stoletja prvič oblikoval v svoji sodobni obliki in analiziral veliko količino eksperimentalnega materiala.

Indeks refrakcije

Glede na matematično definicijo te fizikalne količine je enaka razmerju med dvema hitrostma svetlobe: v vakuumu in v materialu, to je:

n = c / v

Ker je c> v, bo n vedno večji od enega.

Refrakcijski indeks ima različne vrednosti za različne snovi. Na primer, za zrak je skoraj enak 1, za vodo pa 1,33. Vrednost n je odvisna tudi od kemične sestave istega materiala. Na primer, lomni količnik stekla je odvisen od vrste slednjega in se giblje med 1,5 in 1,66.

Poleg lastnosti materiala n se zelo spreminja, če spremenite frekvenco svetlobe v snopu. Refrakcijski kot modre svetlobe je vedno večji od rdeče. Številke v prejšnjem odstavku se nanašajo na rumeni del spektra, ki ga vidi človek (λ ≈ 590 nm).

Optična gostota medija

Ta fizikalna lastnost določa, kako močno medij upočasni hitrost svetlobe. Optična gostota je edinstveno določena z lomnim količnikom. Na primer, voda je optično bolj gosta kot zrak in vsaka vrsta stekla je bolj gosta kot voda.

Če pogledate Snellovo formulo, lahko vidite, da večja kot je optična gostota medija, nižji kot na normalno bo svetloba v njem. Ta zaključek velja ne glede na to, iz katerega medija in v katero svetlobo bo padel žarek. Torej, če upoštevamo mejo voda-zrak, bo lomni kot manjši od vpadnega kota, če se žarek premakne v vodo. Če spremenite smer žarka, bo vpadni kot manjši.

Izziv uporabe Snellovega zakona

Znano je, da žar svetlobe pade na vodno površino pod kotom 32 ^o . Potrebno je določiti lomni kot svetlobe in velikost njegove spremembe, če vpadni kot povečate za 10 ^o .

Količina refrakcije svetlobe je mogoče določiti iz Snellovega zakona. Imamo:

θ ₂ = arcsin (sin (θ ₁ ) * n ₁ / n ₂ )

Ker svetloba pade iz zraka v vodo, potem n ₁ = 1 in n ₂ = 1,33. Ker vemo, da θ ₁ = 32 ^o , dobimo:

θ ₂ = arcsin (sin (32 ^o ) * 1 / 1,33) = 23,48 ^o

Kot lahko vidite, se je kot bistveno zmanjšal. Sedaj izračunamo kot loma žarka, če je θ ₁ = 42 ^o . Z uporabo iste formule dobimo:

θ ₂ = arcsin (sin (42 ^o ) * 1 / 1,33) = 30,21 ^o

Vzemite razliko med dobljenimi koti, dobimo:

30,21 ^o - 23,48 ^o = 6,73 ^o

Dobljeni rezultat pomeni, da spremembe med kotoma vpadnosti in lomom niso linearne. Povečanje vpadnega kota za 10 ^{o je} povzročilo spremembo kota loma le za 6,7 ^o .

Naloga določanja navidezne globine

Mnogi so opazili, da če pogledate dno rezervoarja, se kamni, ki ležijo na njem, in rastočih alg, zdijo blizu površine. Izračunajte, z uporabo zakona loma, ker se resnične in navidezne globine med seboj razlikujejo. Pri tem bomo upoštevali majhne vpadne kote, kar pomeni, da opazovalec gleda navpično navzdol na dno rezervoarja. Spodaj je ustrezna številka.

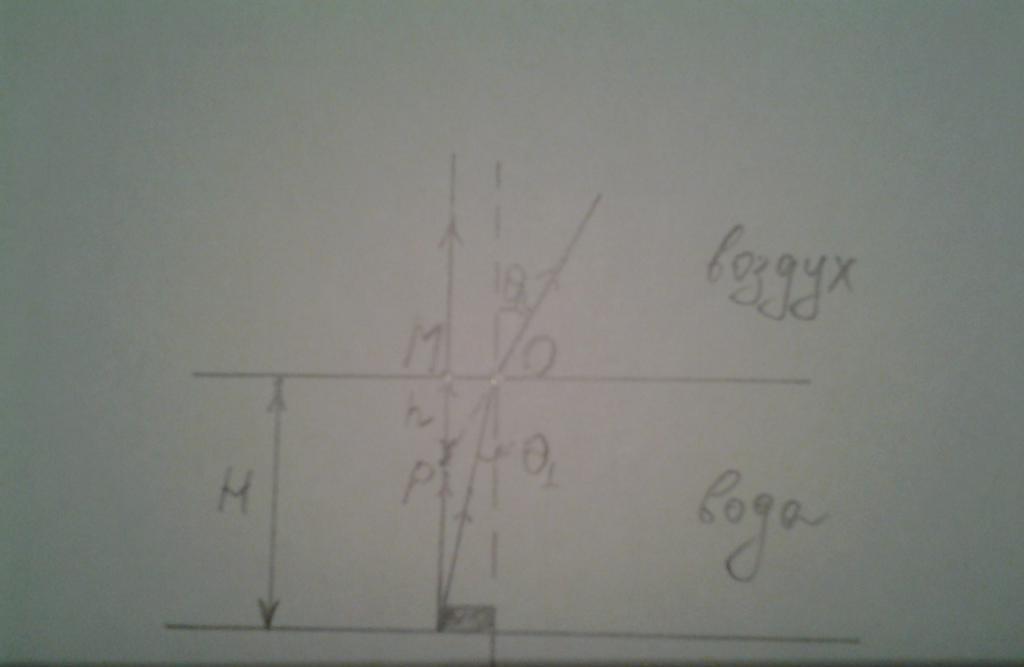
Slika prikazuje predmet, ki leži na dnu. Ker bosta dva žarka, ki prihajajo iz iste točke objekta, sekajo v točki P za opazovalca, bo globina h = MP očitna.

Če želite poiskati h, upoštevajte pravi trikotnik POM. MO interval je H * tg (θ ₁ ), kot POM je 90 - θ2. Zdaj lahko napišete:

tg (90-θ ₂ ) = h / (H * tg (θ ₁ ))

Ker vemo, da je tangens enako razmerju sinusov in kosinusa, in z uporabo formul za trigonometrične funkcije, lahko to enakost prepišemo na naslednji način:

cos (θ ₂ ) / sin (θ ₂ ) = cos (θ ₁ ) * h / (H * sin (θ ₁ ))

Ker upoštevamo majhne kote (blizu vertikale), bodo kosinusi skoraj enaki enotam, zato bo zadnja formula poenostavljena v obliko:

h = h * sin (θ ₁ ) / sin (θ ₂ )

Vendar je razmerje sinusov enako obratnemu razmerju lomnih količnikov medijev po Snellovem zakonu, zato zapišemo:

h = H * n ₂ / n ₁

Ko se žarek premakne iz vode, je n ₂ kazalnik za zrak, ki je enak eni. Končna formula za navidezno globino rezervoarja, če jo gledamo navpično, je:

h = h / n, kjer je n = 1.33

Tako je navidezna globina približno 25% manjša od realne.