Znaki, sestavni elementi in lastnosti enakokrakega trikotnika

Prvi zgodovinarji naše civilizacije - stari Grki - omenjajo Egipt kot rojstno mesto geometrije. Težko se je z njimi ne strinjati, saj vedo, s kakšno izjemno natančnostjo so postavili ogromne grobnice faraonov. Medsebojna razporeditev piramidnih ravnin, njihovih razsežnosti, orientacije vzdolž kardinalnih točk - bi bila nepojmljiva, če bi dosegli takšno popolnost, ne da bi poznali osnove geometrije.

Beseda "geometrija" lahko prevedemo kot "dimenzijo zemlje". In beseda "zemlja" se ne pojavi kot planet - del sončnega sistema, ampak kot ravnina. Označevanje območij za kmetijstvo je najverjetneje začetna osnova znanosti o geometrijskih oblikah, njihovih vrstah in lastnostih.

Trikotnik je najpreprostejša prostorska figura planimetrije, ki vsebuje le tri točke - tocke (ne more biti manj). Osnova temeljev je lahko, zakaj se v njem pojavi nekaj skrivnostnega in starodavnega. Vsevidno oko znotraj trikotnika je eden prvih znanih okultnih znakov, geografija njegove distribucije in časovni okvir pa sta preprosto neverjetna. Od starodavnih egipčanskih, sumerskih, azteških in drugih civilizacij do sodobnejših skupnosti okultnih ljubiteljev, raztresenih po vsem svetu.

Kaj so trikotniki

Običajen vsestranski trikotnik je zaprta geometrijska figura, sestavljena iz treh segmentov različnih dolžin in treh kotov, od katerih noben ni pravilen. Poleg tega obstaja več posebnih vrst.

Akutni trikotnik ima vse kote manj kot 90 stopinj. Z drugimi besedami - vsi koti takšnega trikotnika so ostri.

Desni trikotnik nad katerim so učenci ves čas jokali zaradi obilice izrekov, ima en kot z velikostjo 90 stopinj ali, prav tako imenovano, ravno črto.

Tubutni trikotnik se odlikuje po tem, da je eden od njenih vogalov nejasen, to je njegova magnituda več kot 90 stopinj.

Enakostranični trikotnik ima tri strani enake dolžine. Takšna slika ima tudi vse kote.

Končno, v enakokrako trikotniku s tremi stranicami sta obe enaki.

Posebnosti

Lastnosti enakokrakega trikotnika določajo tudi njegovo glavno, glavno razliko - enakost obeh strani. Te stranice so enake med seboj imenovane stegna (ali, bolj pogosto, stranske strani), tretja pa se imenuje »temelj«.

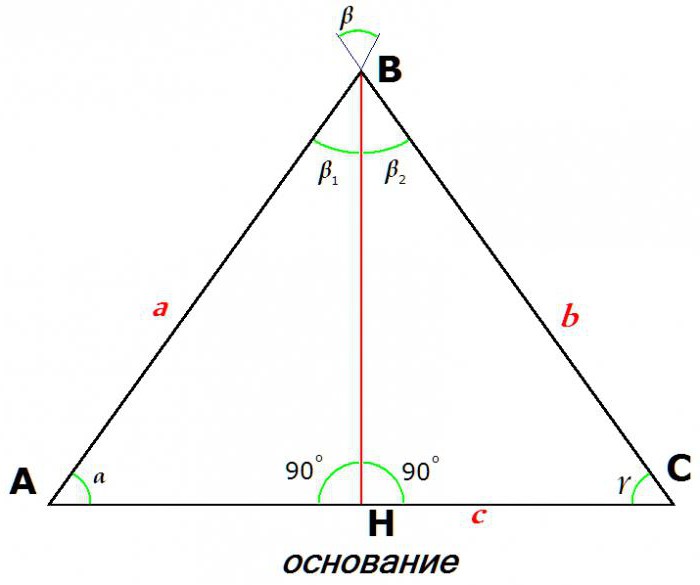
Na tej sliki je a = b.

Drugi znak enakokrakega trikotnika izhaja iz sinusnega izreka. Ker so strani a in b enake, so sinusi njihovih nasprotnih kotov enaki:

a / sin γ = b / sin α, od kod imamo: sin γ = sin α.

Enakost sinusov pomeni enakost kotov: γ = α.

Torej je drugi znak enakokrakega trikotnika enakost dveh kotov, ki mejijo na osnovo.

Tretji znak. Trikotnik razlikuje elemente, kot so višina, simetrala in mediana.

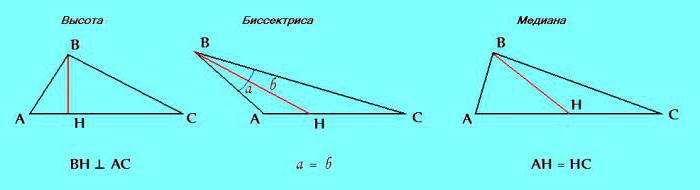
Če se v postopku reševanja problema izkaže, da sta v obravnavanem trikotniku dva od teh elementov enaka: višina z simetrala; simetrala z mediana; mediana z višino - vsekakor je mogoče sklepati, da je trikotnik enakokračen.

Geometrijske lastnosti slike

1. Lastnosti enakokrakega trikotnika. Ena od razlikovalnih lastnosti slike je enakost kotov, ki mejijo na podlago:

α = γ;

<VAS = <BCA.

2. Druga lastnost, o kateri smo že govorili: mediana, simetrala in višina v enakokrakega trikotnika se ujemata, če sta zgrajena od njegovega vrha do osnove.

3. Enakost bisektorjev, vzetih iz tock v bazi:

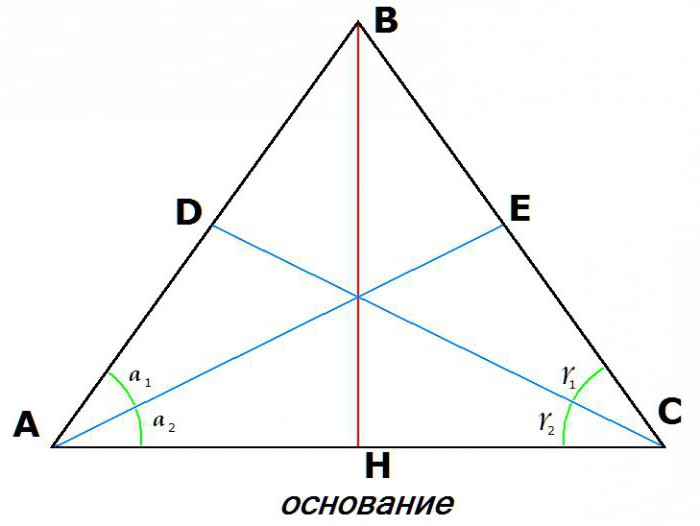
Če je AE simetrala kota YOU, in CD je simetrala kota BCA, potem: AE = DC.

4. Lastnosti enakokrakega trikotnika prav tako zagotavljajo enakost višin, ki se črpajo iz tock v bazi.

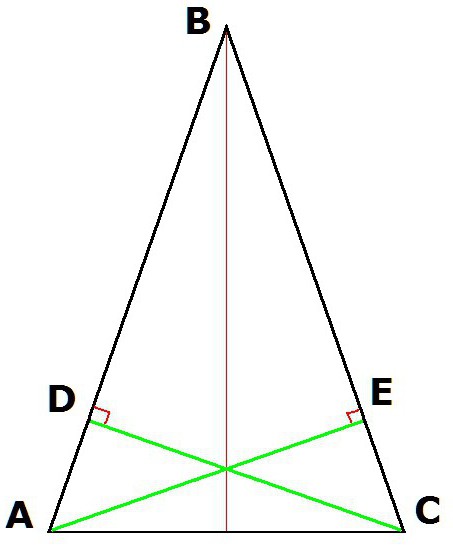
Če zgradimo višine trikotnika ABC (kjer je AB = BC) iz tock A in C, bodo nastali segmenti CD in AE enaki.

5. Mediane, potegnjene iz vogalov v bazi, bodo prav tako enake.

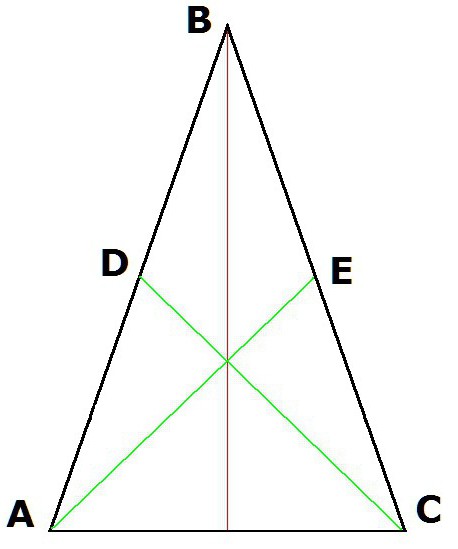
Torej, če sta AE in DC mediana, to je AD = DB in BE = EC, potem AE = DC.

Višina enakokrakega trikotnika

Enakost strani in kotov pri njih dodaja nekatere posebnosti izračunu dolžin elementov obravnavane številke.

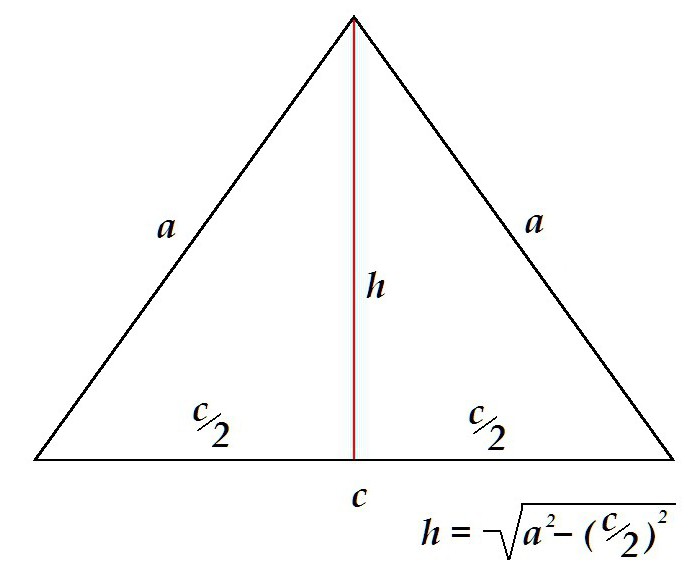
Višina v enakokrakega trikotnika deli sliko na 2 simetrična pravokotna trikotnika s hipotenuzami, v katerih se strani projektirata. Višino v tem primeru določa pitagorejski izrek kot noga.

Trikotnik ima lahko vse tri strani enake, potem pa bo imenovan enakostranični. Višina v enakostraničnem trikotniku je določena na enak način, samo za izračune je dovolj vedeti le eno vrednost - dolžino strani tega trikotnika.

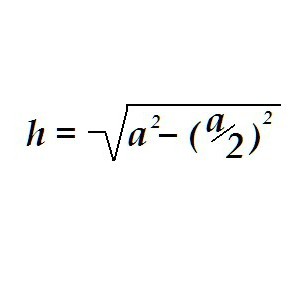
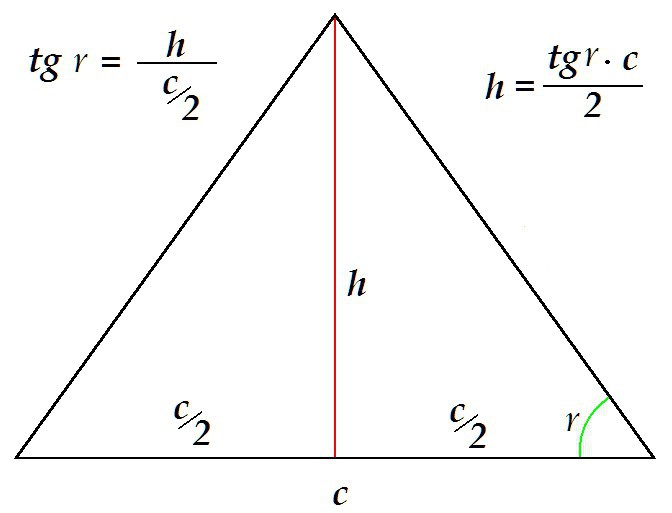
Višino je mogoče določiti na drug način, na primer poznavanje podlage in kota, ki leži ob njem.

Mediana enakokrakega trikotnika

Obravnavani tip trikotnika je zaradi svojih geometrijskih značilnosti precej preprosto rešen z minimalnim nizom izvornih podatkov. Ker je mediana v enakokrakega trikotnika enaka njegovi višini in njeni bisektriki, algoritem za določanje ni drugačen od vrstnega reda, v katerem so ti elementi izračunani.

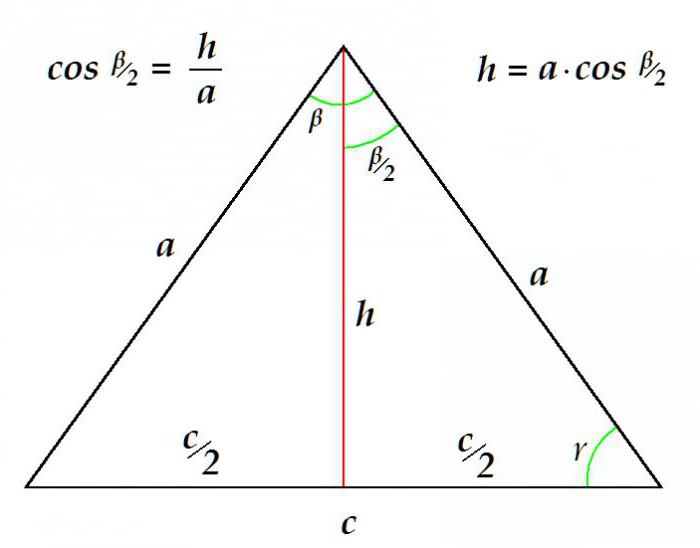
Dolžino mediane lahko na primer določite po znani strani in kotu vozlišča.

Kako določiti obseg

Ker sta v obravnavani planimetrični sliki obe strani vedno enaki, je za določitev oboda zadostno poznati dolžino podnožja in dolžino ene od strani.

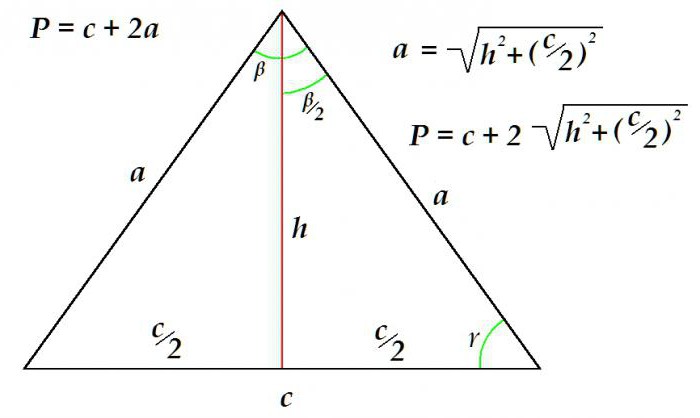
Razmislite o tem, kdaj določiti obseg trikotnika z znano osnovo in višino.

Obod je enak vsoti podnožja in dvojni stranski dolžini. Ta stran pa je določena z uporabo Pitagorejevega izreka kot hipotenuza pravega trikotnika. Njegova dolžina je enaka kvadratni koren vsote kvadratov višine in kvadrata polovice osnove.

Površina enakokrakega trikotnika

Praviloma obstajajo težave in izračun površine enakokrakega trikotnika. Splošno pravilo za določanje površine trikotnika kot polovice produkta osnove na njegovo višino seveda velja tudi v našem primeru. Vendar pa lastnosti enakokrakega trikotnika znova olajšajo delo.

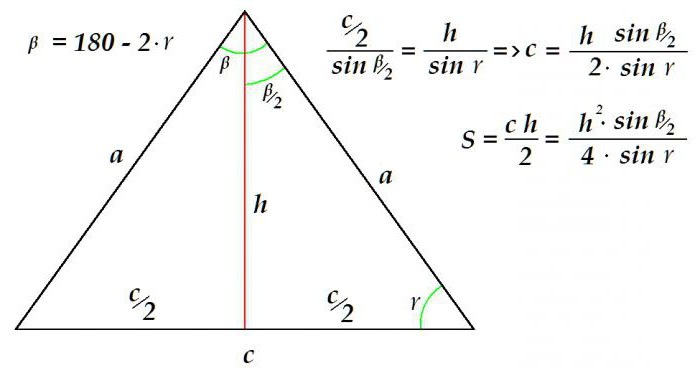
Predpostavimo, da sta višina in kot, ki ležita zraven baze, znana. Potrebno je določiti območje slike. To je mogoče storiti na ta način.

Ker je vsota kotov katerega koli trikotnika 180 °, je enostavno določiti kot. Nadalje, z uporabo razmerja, sestavljenega po sinusnem izreku, je določena dolžina osnove trikotnika. Na voljo so vse, osnova in višina - dovolj podatkov za določitev območja.

Druge lastnosti enakokrakega trikotnika

Položaj središča kroga, opisanega okoli enakokrakega trikotnika, je odvisen od kota vozlišča. Torej, če je enakokračni trikotnik akuten, se središče kroga nahaja znotraj slike.

Središče kroga, ki je opisano okrog enoskotnega trikotnika s topo stranico, leži zunaj njega. In končno, če je kot pod vrhom 90 °, središče leži točno na sredini podlage, premer kroga pa poteka skozi podnožje.

Za določitev polmera kroga, opisanega okoli enakokrakega trikotnika, zadostuje, da dolžino strani razdelimo z dvojnim kosinusom polovice kota na vrh.