Verjetnost dogodka Določanje verjetnosti dogodka

Sprva je bila teorija verjetnosti, saj je bila le zbirka informacij in empiričnih opazovanj iger s kockami, postala trdna znanost. Prvi, ki ji je dal matematični okvir, sta bila Farm in Pascal.

Od razmišljanja o večni teoriji verjetnosti

Dve osebnosti, ki jim teorija verjetnosti dolguje številne temeljne formule, Blaise Pascal in Thomas Bayes, so znani kot globoko religiozni ljudje, ki so prezbiterijanski duhovnik. Očitno je želja teh dveh znanstvenikov, da dokažejo zmotno mnenje o določeni Fortune, ki dajejo sreče svojim hišnim ljubljenčkom, spodbudila raziskave na tem področju. Navsezadnje je vsaka igra na srečo s svojimi dobitki in izgubami le simfonija matematičnih načel.

Zahvaljujoč navdušenju kavalirja Meréja, ki je bil prav tako igralec in oseba, ki ni ravnodušna do znanosti, je bil Pascal prisiljen najti način za izračun verjetnosti. De Mere se je zanimalo za takšno vprašanje: "Kolikokrat boste morali v parih vrgati dve kocki, da bi dobili 12 točk več kot 50%?" Drugo vprašanje, zelo zanima gospod: "Kako deliti stavo med udeleženci nedokončane igre?" Seveda je Pascal uspešno odgovoril na obe vprašanji de Mereja, ki je postal neveden pobudnik razvoja teorije verjetnosti. Zanimivo je, da je persona de Mere ostala znana na tem področju in ne v literaturi.

Prej noben matematik ni poskušal izračunati verjetnosti dogodkov, saj se je mislilo, da je to le odločitev o sramotenju. Blaise Pascal je dal prvo opredelitev verjetnosti dogodka in pokazal, da je to specifična številka, ki jo je mogoče matematično utemeljiti. Teorija verjetnosti je postala osnova za statistiko in se široko uporablja v sodobni znanosti.

Kaj je nesreča

Če upoštevamo test, ki se lahko ponovi neskončno število krat, potem lahko definiramo naključni dogodek. To je eden od verjetnih rezultatov poskusa.

Izkušnje so izvajanje konkretnih ukrepov v nespremenjenih razmerah.

Za delo z rezultati izkušenj, so dogodki običajno označeni s črkami A, B, C, D, E ...

Verjetnost naključnega dogodka

Za prehod na matematični del verjetnosti je potrebno definirati vse njegove komponente.

Verjetnost dogodka je numerično izražena mera možnosti nastanka določenega dogodka (A ali B) kot rezultat izkušnje. Označuje verjetnost kot P (A) ali P (B).

V teoriji verjetnosti se razlikuje:

• zanesljiv dogodek je zagotovljen kot rezultat poskusa P (=) = 1;
• nemogoči dogodek se nikoli ne more zgoditi P (Ø) = 0;
• naključni dogodek je med zanesljivim in nemogočim, kar pomeni, da je verjetnost njegovega nastanka možna, vendar ne zajamčena (verjetnost naključnega dogodka je vedno znotraj 0≤P (A) ≤ 1).

Razmerje med dogodki

Upoštevajte eno in vsoto dogodkov A + B, ko dogodek šteje pri izvajanju vsaj ene od komponent, A ali B, ali oboje - A in B.

Medsebojno so lahko dogodki:

• Enako kot.
• Združljiv.
• Nezdružljivo.
• Nasproti (medsebojno izključujoči se).
• Odvisno.

Če se dva dogodka lahko pojavita z enako verjetnostjo, sta enako mogoča .

Če pojav dogodka A ne izniči verjetnosti pojava dogodka B, so združljivi.

Če se dogodki A in B nikoli ne pojavijo hkrati v isti izkušnji, se imenujejo nezdružljivi . Dober primer je premetavanje kovanca: videz repa je samodejno nepojavljen orel.

Verjetnost za vsoto takih nezdružljivih dogodkov je vsota verjetnosti vsakega dogodka:

Р (А + В) = Р (А) + Р (В)

Če nastop enega dogodka onemogoči, da bi se drugi zgodil, potem se imenujejo nasproti. Potem je ena izmed njih označena kot A, druga pa Ā (bere se kot "ne A"). Pojav dogodka A pomeni, da se Ā ni pojavil. Ta dva dogodka tvorita popolno skupino z vsoto verjetnosti, ki je enaka 1.

Odvisni dogodki imajo medsebojni vpliv, zmanjšujejo ali povečujejo verjetnost drug drugega.

Razmerje med dogodki. Primeri

S primeri je veliko lažje razumeti načela teorije verjetnosti in kombinacijo dogodkov.

Izkušnja, ki jo bomo izvedli, je, da izvlečemo kroglice iz škatle in rezultat vsake izkušnje je osnovni rezultat.

Dogodek je eden od možnih rezultatov izkušnje - rdeča krogla, modra krogla, žogica s številko šest in tako naprej.

Številka preskusa 1. Vpletenih je 6 žogic, od katerih so tri barve modre, nanje so uporabljene lihove številke, preostale tri pa rdeče s parnimi številkami.

Številka preskusa 2. Obstaja 6 modrih kroglic s številkami od enega do šest.

Na podlagi tega primera lahko pokličete kombinacije:

• Zanesljiv dogodek. V španščini Dogodek 2 »dobite modro žogico« je zanesljiv, saj je verjetnost njegovega pojava 1, saj so vse kroglice modre in ni mogoče zamuditi. Medtem ko je dogodek "dobil žogo s številko 1" - naključno.
• Nemogoč dogodek. V španščini №1 z modrimi in rdečimi krogli dogodek "dobili vijolično žogo" je nemogoče, ker je verjetnost njegovega pojava 0.
• Enaki dogodki. V španščini Dogodki številka 1, "dobite žogo s številko 2" in "dobite žogico s številko 3", so prav tako možni, dogodki "dobite žogico s sodo številko" in "dobite žogo s številko 2" pa imajo različno verjetnost.
• Združljivi dogodki. Dvakrat zapored, da bi dobili šest v procesu metanje umreti - to so združljivi dogodki.
• Nezdružljivi dogodki. V istem isp. Dogodki №1 "dobite rdečo žogo" in "dobite žogo z lihim številom" ni mogoče združiti v isti izkušnji.
• Nasproti dogodki. Najbolj jasen primer tega je premetavanje kovancev, ko je vlečenje orla enakovredno ne vleku repov, vsota njihovih verjetnosti pa je vedno 1 (celotna skupina).
• Odvisni dogodki . Torej, v španščini. Št. 1 lahko nastavite, da dvakrat zapored izvlečete rdečo kroglo. Njena ekstrakcija ali ne ekstrakcija prvič vpliva na verjetnost ekstrakcije še enkrat.

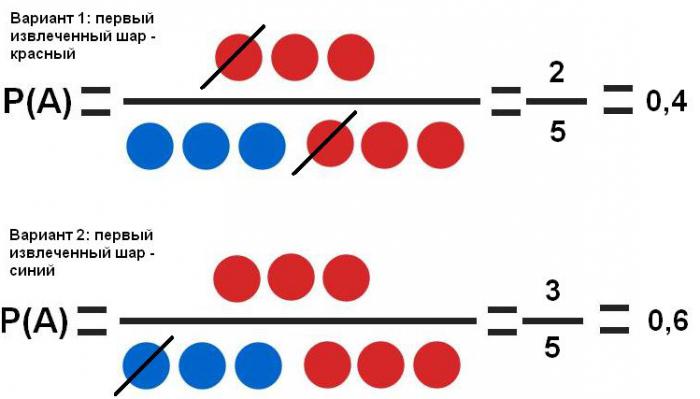
Vidimo, da prvi dogodek pomembno vpliva na verjetnost drugega (40% in 60%).

Formula verjetnosti dogodka

Prehod iz prerokovanja do natančnih podatkov poteka s prenosom teme na matematično ravnino. To pomeni, da se sodbe o naključnem dogodku, kot so "velika verjetnost" ali "minimalna verjetnost", lahko prevedejo v konkretne numerične podatke. Takšen material je že dovoljen za vrednotenje, primerjavo in vstop v bolj zapletene izračune.

Z vidika izračuna je določitev verjetnosti dogodka razmerje med številom osnovnih pozitivnih rezultatov in številom vseh možnih izidov izkušenj glede na določen dogodek. Verjetnost je označena s P (A), kjer P pomeni besedo »probabilit«, ki se iz francoščine prevede kot »verjetnost«.

Torej, formula verjetnosti dogodka:

P (A) = m / n,

Če je m število ugodnih izidov za dogodek A, je n vsota vseh možnih izidov za to izkušnjo. V tem primeru je verjetnost dogodka vedno med 0 in 1:

0 ≤ P (A) ≤ 1.

Izračun verjetnosti dogodka. Primer

Vzemite sp. Št. 1 z žogicami, kot je opisano prej: 3 modre kroglice s številkami 1/3/5 in 3 rdeče s številkami 2/4/6.

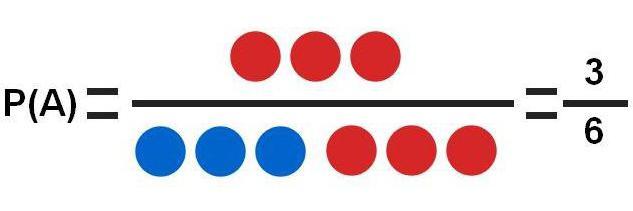
Na podlagi tega preskusa lahko upoštevamo več različnih nalog:

• A - izguba rdeče krogle. Obstajajo 3 rdeče kroglice, skupaj je 6 možnosti, kar je najpreprostejši primer, v katerem je verjetnost dogodka P (A) = 3/6 = 0.5.
• B - izguba parnega števila. Skupno število sodih števil je 3 (2,4,6), skupno število možnih numeričnih možnosti pa je 6. Verjetnost tega dogodka je P (B) = 3/6 = 0.5.
• C - izguba števila, ki je večja od 2. Skupno število možnih izidov je 4 (3,4,5,6) 6. Verjetnost dogodka C je enaka P (C) = 4/6 = 0,67.

Kot je razvidno iz izračunov, je verjetnost dogodka C večja, saj je število verjetnih pozitivnih rezultatov večje kot v A in B.

Neustrezni dogodki

Takšni dogodki se ne morejo istočasno pojaviti v isti izkušnji. Kot v španščini Št. 1 je nemogoče hkrati dobiti modro in rdečo kroglo. To pomeni, da lahko dobite bodisi modro ali rdečo kroglo. Podobno se v kocki celo ne more pojaviti hkrati. liho število.

Verjetnost dveh dogodkov se obravnava kot verjetnost njihove vsote ali produkta. Vsota takih dogodkov A + B se šteje za tak dogodek, ki je sestavljen iz videza dogodka A ali B in produkta njihovega AB - v videzu obeh. Na primer, pojav dveh šestih hkrati na obrazih dveh kock v eni roli.

Vsota več dogodkov je dogodek, ki vključuje pojav vsaj enega izmed njih. Ustvarjanje več dogodkov je skupni nastop vseh.

V teoriji verjetnosti, praviloma, uporaba unije "in" označuje vsoto, združitev "ali" - množenje. Formule s primeri bodo pomagale razumeti logiko seštevanja in množenja v teoriji verjetnosti.

Verjetnost vsote nedoslednih dogodkov

Če se upošteva verjetnost nezdružljivih dogodkov, je verjetnost vsote dogodkov enaka dodatku njihovih verjetnosti:

Р (А + В) = Р (А) + Р (В)

Na primer: izračunajte verjetnost, da je v sp. №1 z modro in rdečimi kroglicami bo padlo iz števila med 1 in 4. Izračunamo ne v eni akciji, ampak vsoto verjetnosti elementarnih komponent. Torej, v tej izkušnji, samo 6 žogic ali 6 vseh možnih rezultatov. Številke, ki izpolnjujejo pogoj, so 2 in 3. Verjetnost 2 izpadanja je 1/6, verjetnost 3 pa je tudi 1/6. Verjetnost, da bo število med 1 in 4 padlo, je enako:

1/6 + 1/6 = 1/3

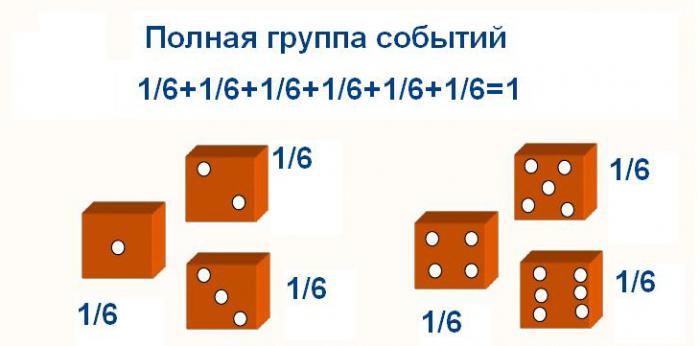
Verjetnost seštevka nezdružljivih dogodkov celotne skupine je 1.

Torej, če v eksperimentu s kocko seštejemo verjetnosti padca vseh števk, potem dobimo eno.

To velja tudi za nasprotne dogodke, na primer v izkušnji z kovancem, kjer je ena stran dogodek A, drugi pa je nasprotni dogodek Ā, kot je dobro znano.

Р (А) + Р (Ā) = 1

Verjetnost nastanka nezdružljivih dogodkov

Množenje verjetnosti se uporabi pri obravnavi pojava dveh ali več nezdružljivih dogodkov v enem opazovanju. Verjetnost, da se dogodki A in B pojavita hkrati, je enaka zmnožku njihovih verjetnosti, ali:

Р (А * В) = Р (А) * Р (В)

Na primer, verjetnost, da je v sp. # 1 kot rezultat dveh poskusov dvakrat se bo pojavila modra žogica, enaka

½ * ½ = ¼

To pomeni, da je verjetnost dogodka, ko se zaradi dveh poskusov z izvlečenjem žogic izvlečejo samo modre žoge, 25%. Zelo enostavno je opraviti praktične poskuse te naloge in preveriti, ali je to res.

Skupni dogodki

Dogodki se štejejo za skupne, če se videz enega od njih lahko ujema s pojavom drugega. Kljub temu, da so skupni, se upošteva verjetnost neodvisnih dogodkov. Na primer, metanje dveh kock lahko daje rezultat, ko se na obeh nanaša številka 6. Čeprav so dogodki sovpadali in so se pojavili sočasno, so neodvisni drug od drugega - lahko pade samo ena šest, druga kost nima vpliva.

Verjetnost skupnih dogodkov se obravnava kot verjetnost njihove vsote.

Verjetnost vsote skupnih dogodkov. Primer

Verjetnost seštevka dogodkov A in B, ki sta skupna drug z drugim, je enaka vsoti verjetnosti dogodka minus verjetnost njihovega dela (tj. Njihovega skupnega izvajanja):

R _spoj. (A + B) = P (A) + P (B) - P (AB)

Predpostavimo, da je verjetnost, da bo tarča udarila z enim strelom, 0,4. Potem dogodek A - udarjanje v cilj v prvem poskusu, B - v drugem. Ti dogodki so skupni, saj je možno, da boste zadeli tarčo s prvega in drugega strela. Toda dogodki niso odvisni. Kolikšna je verjetnost, da se bo dogodek porazil z dvema streljama (vsaj eno)? Po formuli:

0,4 + 0,4-0,4 x 0,4 = 0,64

Odgovor na vprašanje je: "Verjetnost, da bo tarča dvignila dva strela, je 64%."

Ta formula za verjetnost dogodka se lahko uporabi tudi za nezdružljive dogodke, kjer je verjetnost skupnega nastopa dogodka P (AB) = 0. To pomeni, da je verjetnost vsote neskladnih dogodkov lahko obravnavana kot poseben primer predlagane formule.

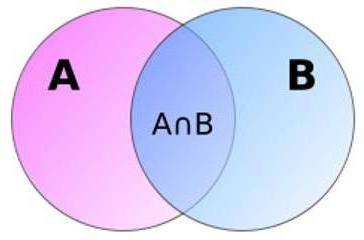
Geometrija verjetnosti zaradi jasnosti

Zanimivo je, da je verjetnost vsote skupnih dogodkov lahko predstavljena v obliki dveh regij A in B, ki se medsebojno sekata. Kot je razvidno iz slike, je območje njihovega združevanja enako skupni površini minus območje njihovega presečišča. Ta geometrijska razlaga na prvi pogled naredi razumevanje nelogične formule. Upoštevajte, da geometrijske rešitve niso redke v teoriji verjetnosti.

Določitev verjetnosti vsote skupnih (več kot dveh) skupnih dogodkov je precej okorna. Če ga želite izračunati, morate uporabiti formule, ki so na voljo za te primere.

Odvisni dogodki

Odvisni dogodki se prikličejo, če pojav enega od njih (A) vpliva na verjetnost nastanka drugega (B). Poleg tega se upošteva vpliv pojavljanja dogodka A in njegovega neprisotnosti. Čeprav se dogodki imenujejo odvisni po definiciji, je le eden od njih odvisen (B). Običajna verjetnost je označena kot P (B) ali verjetnost neodvisnih dogodkov. V primeru odvisnikov se uvede nov koncept - pogojna verjetnost P _A (B), ki je verjetnost odvisnega dogodka B pod pogojem, da se zgodi dogodek A (hipoteza), od katerega je odvisen.

Toda dogodek A je tudi naključen, zato ima tudi verjetnost, ki mora in se lahko upošteva pri izvedenih izračunih. Naslednji primer bo pokazal, kako delati z odvisnimi dogodki in hipotezo.

Primer izračuna verjetnosti odvisnih dogodkov

Dober primer za izračun odvisnih dogodkov je lahko standardna kartica kart.

Na primeru krova s ​​36 kartic upoštevamo odvisne dogodke. Potrebno je določiti verjetnost, da bo druga kartica, ki je bila izvlečena iz krova, iz diamantne obleke, če je prva kartica:

1. Diamanti
2. Še ena obleka.

Očitno je, da je verjetnost drugega dogodka B odvisna od prvega A. Torej, če je prva možnost veljavna, je bila na krovu 1 kartica (35) in 1 diamant (8) manj, verjetnost dogodka B:

P _A (B) = 8/35 = 0,23

Če je druga možnost veljavna, je na krovu 35 kart, celotno število tamburin (9) pa je še vedno ohranjeno, nato pa verjetnost naslednjega dogodka B:

Р _A (V) = 9/35 = 0,26.

Vidimo lahko, da če je dogodek A urejen tako, da je prva kartica tamburina, potem se verjetnost dogodka B zmanjša in obratno.

Množenje odvisnih dogodkov

V skladu s prejšnjim poglavjem sprejmemo prvi dogodek (A) kot dejstvo, če pa govorimo v bistvu, je naključno. Verjetnost tega dogodka, in sicer pridobivanje diamantov iz kart, je enaka:

P (A) = 9/36 = 1/4

Ker teorija ne obstaja sama po sebi, ampak je namenjena za praktične namene, je pošteno opozoriti, da je verjetnost nastanka odvisnih dogodkov najpogosteje potrebna.

V skladu s teoremom o produktu verjetnosti odvisnih dogodkov je verjetnost pojava odvisnih dogodkov A in B enaka verjetnosti enega dogodka A, pomnoženega s pogojno verjetnostjo dogodka B (odvisno od A):

P (AB) = P (A) * P _A (B)

Potem, v primeru s krovom, je verjetnost pridobivanja dveh kart z obleko diamantov:

9/36 * 8/35 = 0,0571 ali 5,7%

In verjetnost ekstrakcije na začetku ni tamburin, potem pa tamburini, je enaka:

27/36 * 9/35 = 0,19 ali 19%

Vidimo, da je verjetnost pojava dogodka B večja, pod pogojem, da se najprej izvleče kartica karte, ki je drugačna od diamantov. Ta rezultat je precej logičen in razumljiv.

Skupna verjetnost dogodka

Ko problem s pogojnimi verjetnostmi postane večplasten, ga ni mogoče izračunati z uporabo običajnih metod. Če obstaja več kot dve hipotezi, in sicer A1, A2, ..., A _n , .. je popolna skupina dogodkov, pod pogojem:

• P (A _i )> 0, i = 1,2, ...
• A _i ∩ A _j = Ø, i ≠ j.
• Σ _k A _k = Ω.

Tako je formula skupne verjetnosti za dogodek B s celotno skupino naključnih dogodkov A1, A2, ..., A _n enaka _:

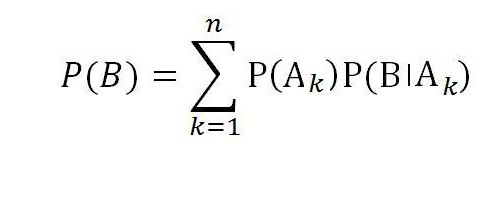
Pogled v prihodnost

Verjetnost naključnega dogodka je bistvena na mnogih področjih znanosti: ekonometrija, statistika, fizika itd. Ker nekaterih procesov ni mogoče določiti deterministično, saj so same po sebi verjetne, so potrebne posebne metode dela. Teorija verjetnosti dogodka se lahko uporabi na katerem koli tehnološkem področju kot način za določitev možnosti napake ali okvare.

Lahko rečemo, da, ko prepoznavamo verjetnost, na neki način naredimo teoretični korak v prihodnost in ga preučimo skozi prizmo formul.