Uvod v dinamično programiranje

Med problemi, ki jih rešujemo s pomočjo matematičnega programiranja, lahko izpostavimo ločen razred problemov, ki zahtevajo optimizacijo večstopenjskih (večstopenjskih) procesov. Takšne naloge se odlikujejo s sposobnostjo razdelitve rešitve na več medsebojno povezanih korakov. Za reševanje takšnih problemov se uporablja dinamično programiranje ali, tako imenovano, večstopenjsko programiranje. Njegove metode so optimizirane za iskanje optimalne rešitve večstopenjskih problemov, ki jih lahko razdelimo na več stopenj, korakov itd.

Izvor izraza

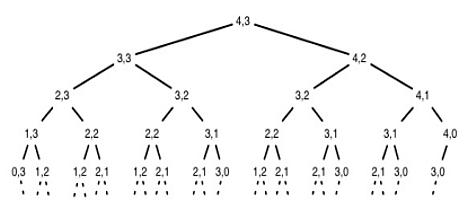
Uporaba besede „dinamični“ v naslovu je sprva predpostavljala, da bi se delitev na podzadnje pojavila predvsem v času. Pri uporabi dinamičnih metod za reševanje produkcijskih, poslovnih in drugih nalog, pri katerih je vpleten časovni dejavnik, prekinitev v ločene stopnje ni težavna. Vendar pa je mogoče uporabiti tehniko dinamičnega programiranja pri nalogah, kjer posamezne faze niso časovno povezane. Vedno v večstopenjski nalogi lahko izberete parameter ali lastnost, v skladu s katerim lahko delite v ločene korake.

Algoritem (metoda) za reševanje večstopenjskih problemov

Algoritem ali Metoda dinamičnega programiranja temelji na načelu zaporedne optimizacije problema, ko je rešitev splošnega problema razdeljena na več rešitev posameznih pododdelkov z naknadno integracijo v eno samo rešitev. Zelo pogosto so posamezne podrejene enake, ena skupna rešitev pa bistveno zmanjša čas izračuna. 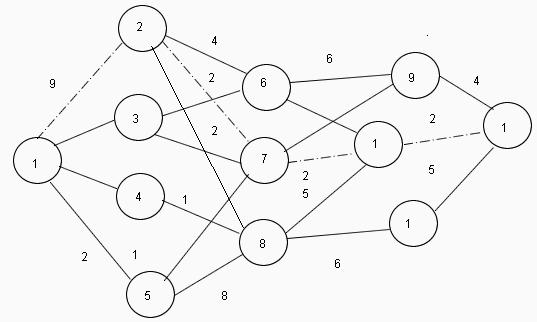Značilnost metode je avtonomnost reševanja problema na vsaki ločeni stopnji, t.j. ne glede na to, kako je bil proces optimiziran in rešen na prejšnji stopnji, trenutni izračun uporablja samo procesne parametre, ki ga trenutno označujejo. Na primer, voznik, ki vozi po cesti, odloči o trenutnem obratu, ne glede na to, koliko ali pred tem je vozil.

Metoda zgoraj in spodnja metoda

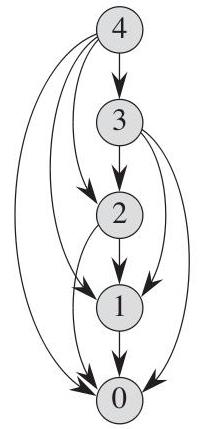
Kljub temu, da pri izračunu na ločeni stopnji reševanja problema uporabimo procesne parametre za trenutni trenutek, rezultat optimizacije na prejšnji stopnji vpliva na izračune naslednjih stopenj, da se doseže najboljši rezultat na splošno. Dinamično programiranje takšno odločitveno načelo imenuje metoda optimalnosti, ki določa, da mora optimalna strategija za reševanje problema, ne glede na začetne odločitve in pogoje, predstavljati optimalno strategijo za začetno stanje v naslednjih fazah. Kot vidimo, je proces reševanja problema kontinuirana optimizacija rezultata na vsaki posamezni stopnji od prve do zadnje. Ta metoda se imenuje metoda zgornjega programiranja. Slika shematično prikazuje algoritem rešitve od zgoraj navzdol. Vendar pa obstaja razred večstopenjskih problemov, v katerem je največji učinek že znan na zadnji stopnji, na primer, že smo prispeli iz točke A v točko B in zdaj želimo vedeti, ali smo šli pravilno na vsaki prejšnji stopnji ali če bi lahko naredili nekaj bolj optimalno. Pojavi se rekurzivno zaporedje stopenj, t.j. gremo kot da je "iz nasprotnega". Ta metoda rešitve se imenuje "metoda spodnjega programiranja".

Praktična uporaba

Dinamično programiranje se lahko uporablja v vseh področju dejavnosti kjer obstajajo procesi, ki so lahko na katerem koli parametru (čas, količina, temperatura itd.), razdeljeni na več enakih majhnih stopenj. Najpogosteje uporabljene dinamične metode reševanja so bile pridobljene v teoriji nadzora in razvoju računalniških sistemov.

Poiščite najboljšo pot

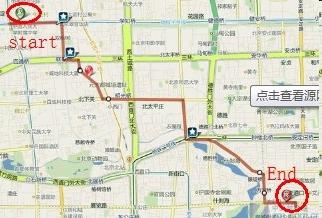
Z dinamično optimizacijo je mogoče rešiti širok razred problemov iskanja ali optimizacije najkrajše poti in drugih problemov, pri katerih »klasična« metoda nabiranja možnih rešitev vodi do povečanja časa izračuna, včasih pa je na splošno nesprejemljiva. Klasičen problem dinamičnega programiranja je problem nahrbtnika: podano je določeno število objektov z določeno maso in stroški, zato je treba izbrati niz predmetov z največjo vrednostjo in maso, ki ne presega volumna nahrbtnika. Klasično štetje vseh možnosti v iskanju optimalne rešitve bo trajalo precej časa, s pomočjo dinamičnih metod pa bo problem rešen v razumnem času. Naloge iskanja najkrajše poti za transportno logistiko so osnovne, dinamične rešitve pa so optimalno primerne za njihovo rešitev. Najenostavnejši primer takšne naloge je izdelava najkrajše poti z avtomobilskim GPS navigatorjem.

Proizvodnja

Dinamično programiranje se pogosto uporablja pri reševanju različnih produkcijskih nalog, kot je upravljanje zalog za vzdrževanje zahtevanega števila komponent v vsakem trenutku, načrtovanje proizvodnega procesa, vzdrževanje opreme in remont, enotna obremenitev osebja, najbolj učinkovito dodeljevanje investicijskih skladov itd. Za reševanje proizvodnih problemov z dinamičnimi metodami programiranja smo razvili posebne programske pakete Vgrajen v priljubljene sisteme za upravljanje podjetij, kot je SAP.

Znanstveno področje

Metode dinamičnega programiranja se pogosto uporabljajo v različnih znanstvenih študijah. Na primer, uspešno se uporabljajo v algoritmih za prepoznavanje govora in slike, pri obdelavi velikih podatkovnih nizov v sociologiji in gospodarske dejavnosti.