Interpolacija je ... Definicija, značilnosti izračuna in primeri interpolacije

Mnogi od nas so se v različnih znanostih soočili z nerazumljivimi izrazi. Vendar pa je zelo malo ljudi, ki se ne bojijo nerazumljivih besed, ampak nas nasprotno spodbujajo in nas silijo, da se vse bolj poglabljamo v predmet, ki ga proučujemo. Danes bomo govorili o taki stvari, kot je interpolacija. To je metoda izdelave grafov iz znanih točk, ki z minimalno količino informacij o funkciji omogoča napovedovanje njenega obnašanja na določenih odsekih krivulje.

Preden se obrnemo na bistvo same definicije in o njej podrobneje povemo, se malo poglobimo v zgodbo.

Zgodovina

Interpolacija je znana že od antičnih časov. Ta fenomen pa svoj razvoj dolguje številnim najpomembnejšim matematikom preteklosti: Newton, Leibniz in Gregory. Ta koncept so razvili s pomočjo naprednejših matematičnih metod, ki so bile takrat na voljo. Pred tem je bila uporabljena in uporabljena interpolacija v izračunih, vendar je bila izvedena v popolnoma netočnih načinih, ki zahtevajo veliko količino podatkov za izdelavo modela, ki je bolj ali manj blizu realnosti.

Danes lahko celo izberemo, katera metoda interpolacije je primernejša. Vse je bilo prevedeno v računalniški jezik, ki z veliko natančnostjo lahko napoveduje obnašanje funkcije na določenem območju, omejeno z znanimi točkami.

Interpolacija je precej ozek pojem, zato njena zgodovina ni tako bogata z dejstvi. V naslednjem razdelku bomo razumeli, kaj je res interpolacija in kako se razlikuje od njenega nasprotja - ekstrapolacija.

Kaj je interpolacija?

Kot smo že povedali, je to splošno ime za načine, kako zgraditi graf po točkah. V šoli se to večinoma opravi z zbiranjem tabele, prepoznavanjem točk na grafu in grobo gradnjo linij, ki jih povezujejo. Zadnje dejanje je narejeno na podlagi presoje podobnosti preiskovane funkcije z drugimi, vrste grafov, ki jih poznamo.

Vendar obstajajo še drugi, bolj zapleteni in natančni načini za izpolnitev naloge načrtovanja po točkah. Interpolacija je torej »napoved« obnašanja funkcije na določenem območju, omejena z znanimi točkami.

Podoben koncept je povezan z istim področjem - ekstrapolacijo. Predstavlja tudi napoved grafa funkcije, vendar onstran znanih točk grafa. S to metodo se napoved izvede na podlagi obnašanja funkcije na znani interval, nato pa se ta funkcija uporabi tudi za neznani interval. Ta metoda je zelo primerna za praktično uporabo in se aktivno uporablja na primer v ekonomiji za napovedovanje vzponov in padcev na trgu ter napovedovanje demografskih razmer v državi.

Vendar smo se oddaljili od glavne teme. V naslednjem razdelku bomo razumeli, kakšno vrsto interpolacije se zgodi in s katerimi formulami lahko izvedete to operacijo.

Vrste interpolacije

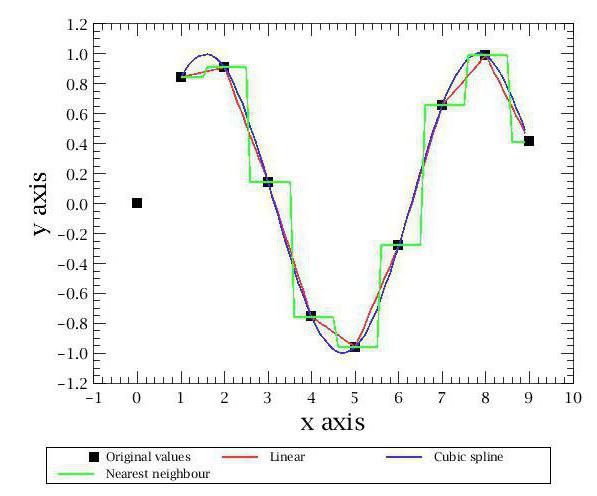
Najenostavnejši tip je interpolacija najbližjega soseda. S to metodo dobimo zelo približen graf iz pravokotnikov. Če ste vsaj enkrat videli razlago geometrijskega pomena integrala na grafu, boste razumeli, o kakšni grafični obliki govorimo.

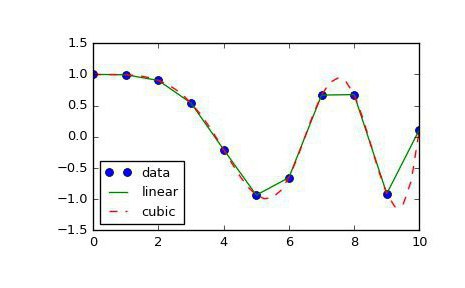
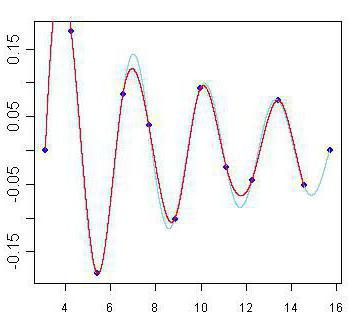
Poleg tega obstajajo tudi druge metode interpolacije. Najbolj znani in priljubljeni so povezani s polinomi. Bolj natančni so in omogočajo napovedovanje obnašanja funkcije s precej slabim naborom vrednosti. Prva interpolacijska metoda, ki jo bomo upoštevali, bo linearna interpolacija s polinomi. To je najlažji način iz te kategorije in zagotovo je vsak od vas to uporabil v šoli. Njegovo bistvo je v konstrukciji ravnih črt med znanimi točkami. Kot je znano, poteka ena ravna črta skozi dve točki ravnine, katere enačbo lahko najdemo na podlagi koordinat teh točk. Z gradnjo teh ravnih linij dobimo zlomljen graf, ki je nekako, vendar odraža približne vrednosti funkcij in na splošno sovpada z realnostjo. Tako izvajamo linearno interpolacijo.

Zapletene vrste interpolacije

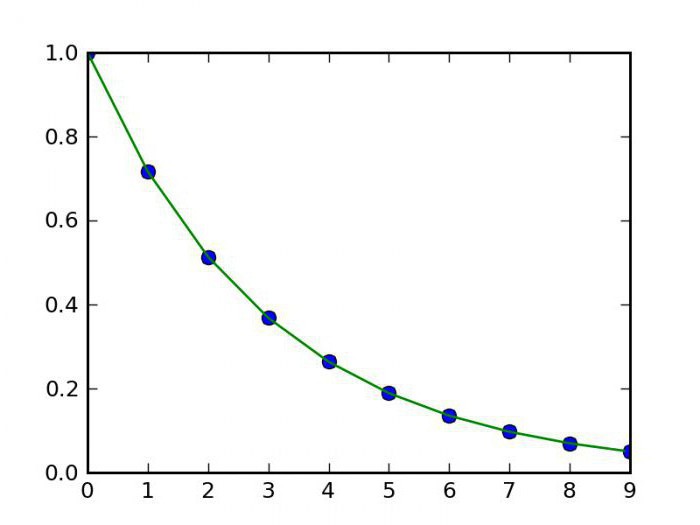
Obstaja bolj zanimiva, vendar bolj zapletena metoda interpolacije. Izumil ga je francoski matematik Joseph Louis Lagrange. Zato je izračun interpolacije z uporabo te metode po njem imenovan: Lagrangova interpolacija. Pri tem je poudarek na tem: če metoda, opisana v prejšnjem odstavku, za izračun uporablja samo linearno funkcijo, potem Lagrangeova razgradnja vključuje tudi uporabo polinomov višjih stopenj. Vendar pa ni preprosto najti samih interpolacijskih formul za različne funkcije. In več točk je znanih, bolj natančna je formula za interpolacijo. Vendar obstaja še veliko drugih metod.

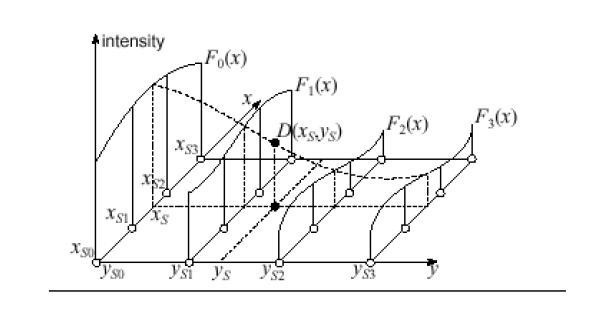
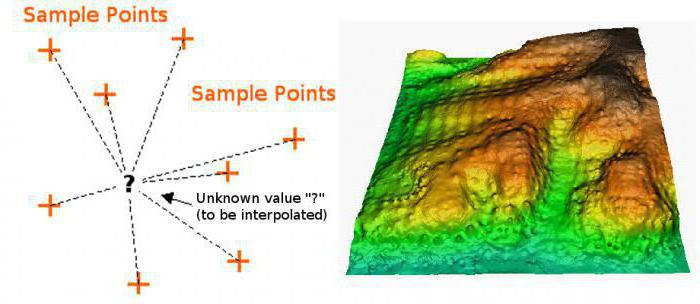
Obstaja tudi bolj popolna in realistična metoda izračuna. Uporabljena interpolacijska formula je niz polinomov, katerih uporaba je odvisna od območja funkcije. Ta metoda se imenuje funkcija spline. Poleg tega obstajajo tudi načini za izvedbo take funkcije, kot so interpolacijske funkcije dveh spremenljivk. Obstajata samo dve metodi. Med njimi je bilinearna ali dvojna interpolacija. Ta metoda vam omogoča enostavno izdelavo grafa s točkami v tridimenzionalni prostor. Druge metode ne bodo vplivale. Na splošno je interpolacija univerzalno ime za vse te grafične metode, vendar jih je mogoče razdeliti v skupine glede na vrsto funkcije, ki je predmet tega dejanja. To pomeni, da se interpolacija, primer, ki smo jo obravnavali zgoraj, nanaša na neposredne metode. Obstaja tudi inverzna interpolacija, ki se razlikuje v tem, da nam omogoča izračun ne neposredne, ampak inverzne funkcije (to je x iz y). Najnovejših možnosti ne bomo upoštevali, saj je to precej težko in zahteva dobro matematično bazo znanja.

Obračamo se morda na enega najpomembnejših delov. Iz nje se učimo, kako in kje se v življenju uporablja nabor metod, o katerih razpravljamo.

Uporaba

Matematika je znana kot kraljica znanosti. Torej, tudi če prvič ne vidite točke v nekaterih operacijah, to ne pomeni, da so neuporabne. Na primer, zdi se, da je interpolacija neuporabna stvar, s pomočjo katere lahko zgradimo samo grafe, ki jih malo ljudi potrebuje zdaj. Vendar je pri vsakem izračunu v inženirstvu, fiziki in mnogih drugih znanostih (npr. Biologiji) izredno pomembno zagotoviti dokaj popolno sliko pojava, medtem ko ima določeno vrsto vrednot. Vrednosti, razpršene vzdolž grafa, ne dajejo vedno jasne predstave o obnašanju funkcije na določenem območju, vrednostih njenih izvedenih delov in presečiščih z osmi. In to je zelo pomembno za mnoga področja našega življenja z vami.

In kako je to koristno v življenju?

Na to vprašanje je zelo težko odgovoriti. Toda odgovor je preprost: nikakor ne. To znanje vam ne bo koristno. Toda če razumete ta material in metode, po katerih se ta dejanja izvajajo, boste prakticirali svojo logiko, ki je zelo uporabna v življenju. Glavna stvar ni znanje, ampak spretnosti, ki jih oseba pridobi v procesu učenja. Konec koncev, ni čudno, da obstaja beseda: "Živite in se učite."

Sorodni pojmi

Sami lahko razumete, kako pomembno je (in še vedno ne izgublja pomena) to področje matematike, pri čemer gledamo na raznolikost drugih konceptov, povezanih s tem. O ekstrapolaciji smo že govorili, vendar obstaja tudi približek. Morda ste že slišali to besedo. V vsakem primeru, kaj to pomeni, smo razpravljali tudi v tem članku. Približevanje, kot je interpolacija, je koncept, ki se nanaša na konstruiranje grafov funkcij. Toda razlika med prvo in drugo je, da predstavlja približno konstrukcijo grafa, ki temelji na podobnih znanih grafih. Ta dva pojma sta si zelo podobna in bolj zanimivo je preučiti vsakega od njih.

Zaključek

Matematika ni tako kompleksna znanost, kot se zdi na prvi pogled. To je precej zanimivo. In v tem članku smo vam skušali dokazati. Pregledali smo koncepte, povezane z konstrukcijo grafov, spoznali smo, kaj je dvojna interpolacija in razstaviti s primeri, kjer se uporablja.