Kako najti dolžino loka kroga

Formula za iskanje dolžine kroga je dokaj preprosta in zelo pogosto pri pomembnih preizkusih, kot je enotni državni izpit, obstajajo takšne težave, ki jih ni mogoče rešiti brez njene uporabe. Prav tako ga morate poznati za mednarodne standardizirane teste, kot so SAT in drugi.

Kakšna je dolžina loka kroga?

Formula je naslednja:

l = πrα / 180 °

Kaj je vsak od elementov formule:

• l je dolžina loka kroga;
• π je število pi (konstantna vrednost je enaka ≈ 3.14);
• r je polmer danega kroga;
• α je vrednost kota, na katerem stoji lok (osrednji in ne vpisan).

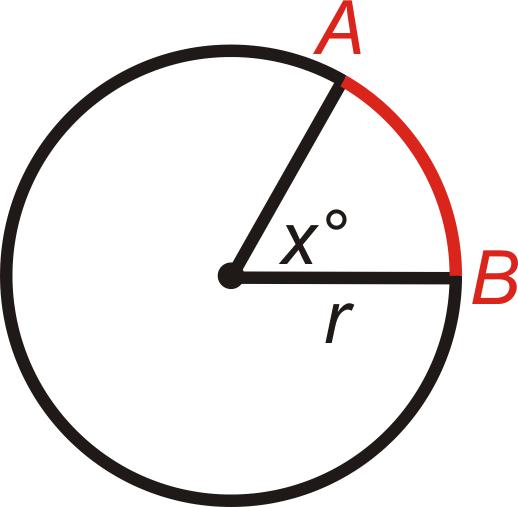
Kot lahko vidite, mora pogoj za rešitev problema vsebovati r in α. Brez teh dveh vrednosti dolžine loka ni mogoče najti.

Kako izhaja ta formula in zakaj je videti tako?

Vse je zelo enostavno. To bo postalo veliko jasnejše, če v imenovalcu postavite 360 ​​° in v števec dodate spredaj dvojico. Lahko tudi α ne pustite v frakciji, ga umaknete in napišete z znakom množenja. Popolnoma je mogoče privoščiti, saj je ta element v števcu. Nato bo splošni pogled:

l = (2πr / 360 °) × α

Samo zaradi udobja, zmanjšana za 2 in 360 °. Zdaj pa, če pogledate natančno, lahko opazite dobro poznano formulo za dolžino celotnega kroga, in sicer 2πr. Celoten krog je sestavljen iz 360 °, ker merilo dobimo na 360 delov. Potem pomnožimo s številom α, to je s številom "kosov pogače", ki jih potrebujemo. Toda vsi vemo zagotovo, da številke (tj. Dolžine celega kroga) ni mogoče deliti s stopinjami. Kaj storiti v tem primeru? Običajno se stopnja praviloma zmanjša s stopnjo osrednjega kota, torej z α. Navsezadnje ostanejo samo številke, rezultat pa je končni odgovor.

To lahko pojasni, zakaj je dolžina loka kroga na ta način in ima to obliko.

Primer problema povprečne kompleksnosti z uporabo te formule

Pogoj: Obstaja krog s polmerom 10 centimetrov. Merilo stopnje osrednjega kota je 90 °. Poiščite dolžino loka kroga, ki ga tvori ta kot.

Rešitev: l = 10π × 90 ° / 180 ° = 10π × 1/2 = 5π

Odgovor: l = 5π

Možno je tudi, da se namesto merila stopnje doda meritev radijanskega kota. V nobenem primeru se ne bojte, ker je tokrat naloga postala veliko lažja. Če želite pretvoriti radian v merilo stopnje, morate to število pomnožiti za 180 ° / π. Torej, zdaj lahko nadomestite naslednjo kombinacijo namesto α : m × 180 ° / π. Kjer je m radijanska vrednost. Potem se 180 in število π zmanjšata in dobimo popolnoma poenostavljeno formulo, ki izgleda takole:

l = mr,

kjer:

• l je dolžina loka kroga;
• m je radiansko merilo kota;
• r je polmer danega kroga.