Ravnotežno stanje vzvoda. Pravilo trenutkov. Enostavni mehanizmi. Naloge in rešitve

Od nekdaj je človeštvo uporabljalo različne mehanizme, ki so namenjeni lažjemu fizičnemu delu. Eden od njih je vzvod. Kaj je to, kakšna je njegova uporaba in kakšen je pogoj ravnovesja vzvoda, je ta članek namenjen obravnavi vseh teh vprašanj.

Kdaj je človeštvo začelo uporabljati načelo vzvoda?

Težko je natančno odgovoriti na to vprašanje, saj so stari Egipčani in prebivalci Mezopotamije že tri tisoč let pred našim štetjem poznali preproste mehanizme.

Eden od teh mehanizmov je tako imenovani vzvodni žerjav. Predstavljal je dolg pol, ki se je nahajal na opori. Slednji je bil nameščen bliže enem koncu droga. Proti koncu, ki je bil dlje od referenčne točke, so vezali posodo, na drugi pa so postavili protiutež, na primer kamen. Sistem je bil prilagojen tako, da je napolnjena posoda privedla do vodoravnega položaja pola.

Dvigalo je služilo za dviganje vode iz vodnjaka, reke ali druge depresije na raven, kjer je bila oseba. Z uporabo majhne sile na plovilo jo je spustil na vodni vir, plovilo je bilo napolnjeno s tekočino, nato pa je z manjšo silo na drugi konec droga s protiutežjo mogoče dvigniti označeno posodo.

Legenda o Arhimedu in ladji

Vsi poznajo antičnega grškega filozofa iz mesta Sirakuze, Arhimeda, ki v svojih delih ni opisal le načela delovanja preprostih mehanizmov (vzvod, nagnjena plošča), temveč tudi ustrezne matematične formule. Do danes je njegov stavek še vedno znan:

Dajte mi oporo in premaknil bom ta svet!

Kot veste, mu nihče ni dal take podpore in Zemlja je ostala na svojem mestu. Vendar pa je bilo tisto, kar je Arhimed res lahko premaknil, ladja. Ena od legend o Plutarhu (delo "Paralelni zivi") pravi naslednje: Arhimed, v pismu svojemu prijatelju, kralju Hieronu iz Sirakuze, je povedal, da lahko sam pod dolocenimi pogoji premakne samovoljno veliko težo. Hieron je bila taka izjava filozofa presenečena in ga prosila, da pokaže, o čem govori. Arhimed se je strinjal. V enem dnevu je bila ladja Hieron v pristanišču natovorjena z ljudmi in sodi, napolnjenimi z vodo. Filozof, ki je sedel na oddaljenosti od ladje, ga je lahko dvignil nad vodo in potegnil vrv, medtem ko je vložil malo napora.

Komponente vzvoda

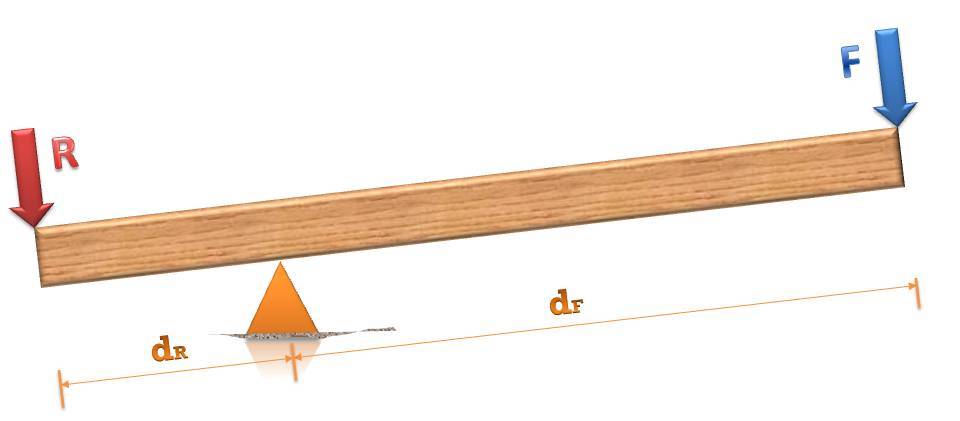
Kljub temu, da govorimo o dokaj preprostem mehanizmu, ima še vedno določeno napravo. Fizično je sestavljen iz dveh glavnih delov: droga ali nosilca in opore. Pri obravnavanju istih nalog se pol šteje kot objekt, ki je sestavljen iz dveh (ali enih) rok. Ram je del pola, ki je glede na oporo na eni strani. V načelu delovanja obravnavanega mehanizma ima veliko vlogo natanko dolžina rame.

Ko upoštevamo vzvod v delu, potem obstajata še dva dodatna elementa: uporabljena sila in moč, da jo preprečimo. Prvi skuša sprožiti predmet, ki ustvarja silo nasprotovanja.

Ravnotežno stanje finančnega vzvoda v fiziki

Seznanimo se z napravo tega mehanizma in predstavimo matematično formulo, s katero lahko rečemo, katera roka vzvoda se bo premaknila v katero smer ali, nasprotno, celotna naprava bo mirovala. Formula ima obliko:

F ₁ * l ₁ = F ₂ * 1 ₂ ,

kjer sta F ₁ in F ₂ sila delovanja in reakcija, l ₁ in l ₂ sta dolžini krakov, na katere se te sile uporabljajo.

Ta izraz omogoča raziskovanje ravnotežnih pogojev vzvoda, ki ima os vrtenja. Torej, če je rama l ₁ večja od l ₂ , potem za izravnavo sile F ₂ potrebujete manjšo vrednost F ₁ . Nasprotno, če je l ₂ > l ₁ , potem za preprečevanje sile F ₂ morate pritrditi velik F1. Te sklepe je mogoče doseči s ponovnim zapisom zgoraj navedenega izraza v naslednji obliki:

F ₁ / F ₂ = l ₂ / l ₁ .

Kot je razvidno, so sile, ki so vključene v proces oblikovanja ravnotežja, obratno povezane z dolžino ročic vzvoda.

Kakšen je dobiček in izguba pri uporabi vzvoda?

Pomemben zaključek sledi iz zgornjih formul: s pomočjo dolge roke in majhnega napora se lahko premikajo predmeti z veliko maso. To je res, in mnogi mislijo, da uporaba vzvoda vodi k pridobivanju dela. Ampak ni. Delo je količina energije, ki je ni mogoče ustvariti iz nič.

Analizirajmo delo enostavnega vzvoda, ki ima dva strjevanja l ₁ in l ₂ . Recimo, da je na koncu pleča l2 teža P (F2 = P). Na koncu druge rame oseba uporabi silo F ₁ in to obremenitev dvigne na višino h. Zdaj, izračunajmo delo vsake sile in izenačimo dobljene rezultate. Dobimo:

F ₁ x = F ₂ * h.

Sila F _{2 je} delovala vzdolž vertikalne poti dolžine h, F _{1 pa je} delovala tudi vzdolž vertikale, vendar je bila že pritrjena na drugo roko, katere konec se je premikal z neznano količino x. Da bi jo našli, je treba v zadnjem izrazu nadomestiti formulo povezave med silami in ročicami vzvoda. Če izrazimo x, imamo:

x = F ₂ * h / F ₁ = l ₁ * h / l ₂ .

Ta enakost kaže, če je l ₁ > l ₂ , potem F ₂ > F ₁ in x> h, to pomeni, da uporabite majhno silo, lahko dvignete obremenitev z veliko težo, vendar morate ustrezno ročico (l ₁ ) premakniti na večjo. razdaljo. Nasprotno, če je l ₁ <l ₂ , potem je F ₂ <F ₁ in x <h, to pomeni, da se lahko teža določene teže dvigne na višjo višino h s premikom rame l ₁ na manjšo amplitudo, vendar morate uporabiti dovolj veliko silo F ₁ . V prvem primeru dobimo moč v drugem v smeri ali hitrosti.

Ročica torej nima koristi pri delu, omogoča le prerazporeditev bodisi v korist manjše uporabljene sile bodisi v korist večje amplitude gibanja predmeta. Splošno filozofsko načelo deluje na obravnavani temi fizike: vsak dobiček se kompenzira z določeno izgubo.

Vrste vzvodov

Glede na točko uporabe sile in na položaj podpore se razlikujejo naslednje vrste tega mehanizma: t

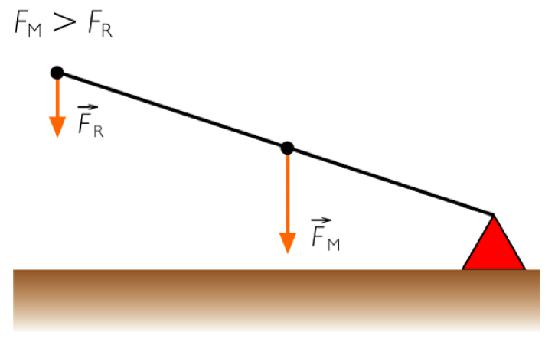
• Prva vrsta: točka je med dvema silama F ₁ in F ₂ , zato bo dolžina rok določila, kaj daje takšno prednost. Primer so navadne škarje.
• Druga vrsta. Tu se sila, s katero se opravlja delo, nahaja med podporo in uporabljeno silo. Ta vrsta gradnje pomeni, da bo vedno pridobila moč in izgubo pri potovanju in hitrosti. Njegov primer je vrtni avto.
• Tretja vrsta. Zadnja možnost, ki jo je še treba uresničiti v tej preprosti zasnovi, je položaj uporabljene sile med podporo in silo upora. V tem primeru je dobiček na poti, vendar je izguba v veljavi. Primer je pinceta.

Koncept trenutka sile

Upoštevanje morebitnih problemov v mehaniki, ki vključujejo koncepte osi ali točke vrtenja, se izvaja z uporabo pravila momenta sile. Ker je podpora vzvoda tudi os (točka), okoli katere se sistem vrti, se tudi sila uporabi za oceno ravnovesja tega mehanizma. S tem je mišljena količina v fiziki, ki je enaka zmnožku ramena in sile, ki deluje:

M = l * F.

Glede na to definicijo se lahko stanje ravnotežnega vzvoda spremeni na naslednji način:

M ₁ = M ₂ , kjer je M ₁ = l ₁ * F ₁ in M ₂ = l ₂ * F ₂ .

Trenutek M je aditiven, kar pomeni, da je skupni moment sile za zadevni sistem mogoče dobiti z običajnim dodajanjem vseh trenutkov M _{i, ki} delujejo na to. Vendar pa je treba upoštevati njihov znak (sila, zaradi katere se sistem obrne v nasprotni smeri urinega kazalca, ustvari pozitiven trenutek + M, in obratno). S tem bo pravilo trenutkov za vzvod, ki je v ravnovesju, videti takole:

M1-M2 = 0.

Ročica izgubi ravnotežje pri M _{1 2} M ₂ .

Kje se uporablja načelo finančnega vzvoda?

Navedli smo že nekaj primerov uporabe tega preprostega in znanega mehanizma iz antičnih časov. Tu je nekaj dodatnih primerov:

• Klešče: vzvod prve vrste, ki vam omogoča, da ustvarite ogromno napora zaradi majhne dolžine ramen l _2, kjer se nahajajo zobje orodja.
• Odpirači pokrovi pločevinke in steklenice: to je vzvod 2. vrste, tako da vedno daje dobiček v naporu.
• Ribiška palica: vzvod 3. vrste, ki vam omogoča premikanje konca ribiške palice s plovcem, grezilo in kavelj za velike amplitude. Izguba v tem primeru se pojavi, ko ribič težko dobi ribe iz vode, tudi če teža ne presega 0,5 kg.

Človek sam s svojimi sklepi, mišicami, kostmi in kitami je živ primer primernega sistema z različnimi vzvodi.

Reševanje problemov

Ravnotežno stanje vzvoda, obravnavanega v članku, se uporablja za reševanje preprostih problemov. Potrebno je izračunati približno dolžino vzvodne ročice, pri čemer je treba vložiti napor, do konca katerega je lahko Archimed s tem dvignil ladjo, kot jo opisuje Plutarh.

Da bi to rešili, predstavimo naslednje predpostavke: upoštevamo grško triremo 90 ton s premikom in predpostavimo, da je bila podpora vzvoda 1 meter od središča mase. Kot bi Arhimed, po legendi, z lahkoto dvignil ladjo, bomo domnevali, da je v ta namen uporabil silo, ki je bila enaka polovici njegove teže, to je okoli 400 N (za maso 82 kg). Nato z uporabo ravnotežnega stanja vzvoda dobimo:

F ₁ * l ₁ = F ₂ * l ₂ => l ₁ = F ₂ * l ₂ / F ₁ = m * g * l ₂ / F ₁ = 90000 * 9,81 * 1/400 ≈ 2,2 km.

Tudi če povečamo silo, ki se uporablja za vrednost same teže Arhimeda in dvakrat podpremo podporo, bo dolžina rame okoli 500 metrov, kar je tudi velika vrednost. Verjetno je legenda o Plutarhu pretiravanje, da bi dokazali učinkovitost vzvoda, in Arhimed ni dejansko dvignil ladje nad vodo.