Dinamika in kinematika krožnega gibanja: formule in reševanje tipičnega problema

Sposobnost opisa gibanja v krogu je pomembna za izračun tehničnih lastnosti vrtljivih gredi in zobnikov. Tovrstna gibanja se pojavljajo tudi v vsakdanjem življenju in naravi, kot je rotacija planetov okoli sonca in drsalcev med nastopi na športnih tekmovanjih. V tem članku bomo preučili, kako lahko z vidika fizike tovrstno gibanje opišemo.

Dinamika rotacije

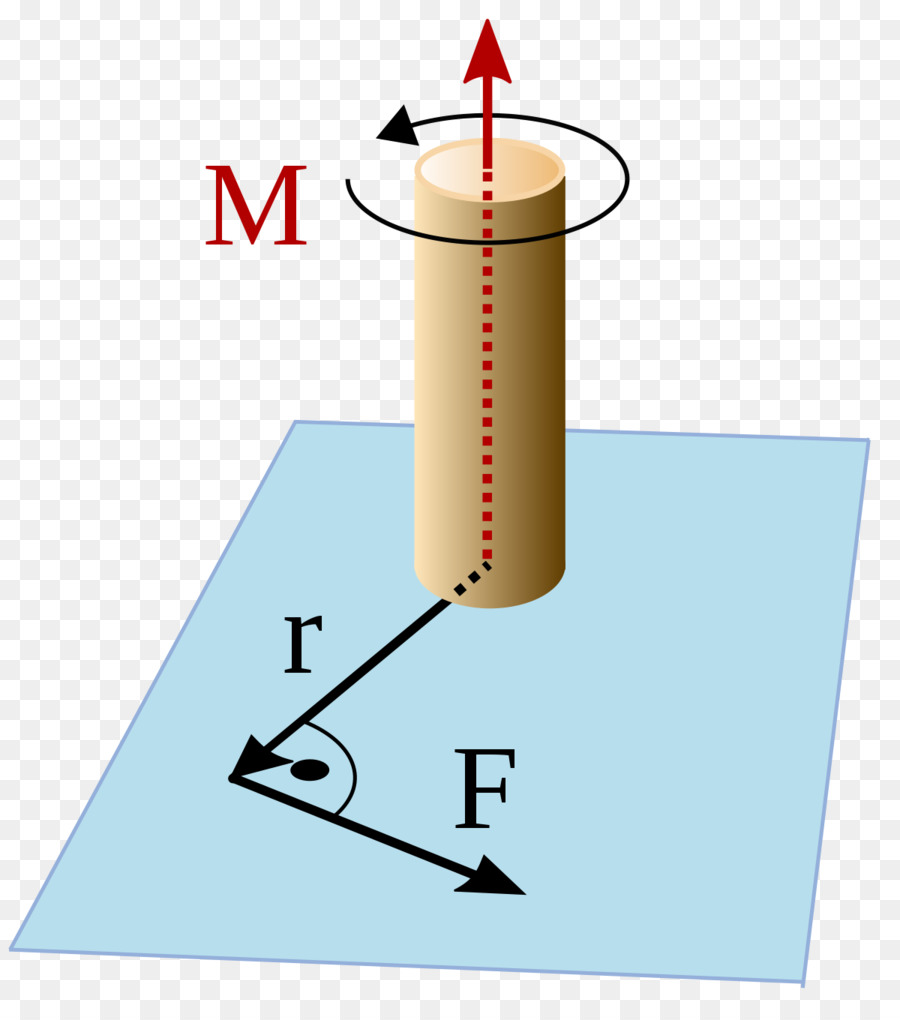
Gibanje v krogu je rotacija določenega telesa ali materialne točke okoli osi. Da bi se telo začelo vrteti, je potrebno imeti zunanji navor, ki deluje na zadevni sistem. Ta trenutek je določen s formulo:

M = F * d

Tu je F sila, d je dolžina vzvoda (razdalja med osjo in točko uporabe sile). Trenutek sile je vektorska vrednost. Formula se uporablja za izračun modula M.

Učinek trenutka M se odraža na sistemu v obliki videza kotnega pospeška. To pomeni, da se sistem začne vrteti. Glavna formula krožnega gibanja je napisana kot:

M = I * α

Tu je I trenutek vztrajnosti, α je kotni pospešek. Obe količini imata analoge za linearno zadevo. Če je vse jasno z analogom vrednosti α, potem je treba za trenutek vztrajnosti pojasniti. Vrednost I odraža inercialne lastnosti vrtljivega sistema. To pomeni, da med rotacijo igra isto vlogo kot navadna telesna teža.

Upoštevajte, da je zgornji izraz analogija Newtonovega drugega zakona za rotacijo.

Centripetalne in centrifugalne sile, pospešek

Proces vrtenja pomeni prisotnost neke notranje sile, ki bi zagotovila krivo gibanje telesa. Ta sila se imenuje centripetal. V skladu z imenom je vedno usmerjen od telesa do osi vrtenja. Ker je dolžina vzvoda d nič, to ne vodi do pojavljanja kotnega pospeška α. Kljub temu pa spreminja vektor linearne hitrosti, torej ustvarja pospešek.

Pospešek pri gibanju v krogu brez spreminjanja modula linearne hitrosti se imenuje centripetal. Izračuna se po formuli:

a _c = v2 / r

Pri čemer je v linearna hitrost materialne točke, ki se vrti na razdalji r od osi.

Poleg centripetalnega lahko pogosto slišite o centrifugalni sili. Slednji želi izvleči telo iz krožne poti do ravne črte. Razlog za njegovo pojavljanje so inercijske lastnosti vrtljivega sistema.

Pri gibanju v krogu so centripetalne in centrifugalne sile enakovredne enake druge in v smeri, v kateri so nasprotne.

Kinematične enačbe vrtenja

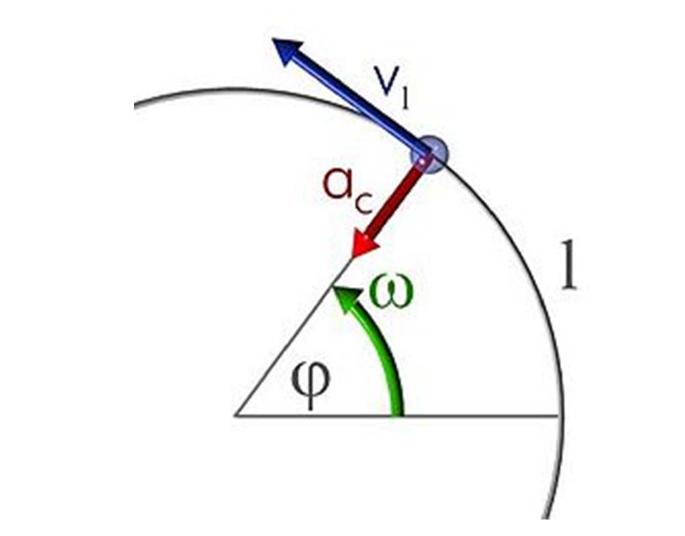
Gibanje v krogu, kot v ravni črti, je lahko enakomerno ali se pojavi s pospeškom. V prvem primeru je formula:

θ = ω * t

To pomeni, da je osrednji kot θ, na katerem se telo obrne v času t, neposredno proporcionalen kotni hitrosti ω. Kot θ je izražen v radianih, hitrost ω pa je izražena v radianih na sekundo.

Če konstanten zunanji moment sil deluje na sistem, se gibanje v krogu zgodi z nekaj konstantnim pospeškom α. V tem primeru velja naslednji kinematični izraz:

θ = α * t 2/2

Če se sistem najprej zavrti z določeno hitrostjo ω _0, nato pa začne povečevati svojo rotacijsko frekvenco s pospeškom α, potem, od trenutka t, ko se pojavi pospešek, bo formula veljavna:

θ = ω ₀ * t + α * t 2/2

Upoštevajte, da je ta izraz linearna kombinacija prejšnjih dveh.

Razmerje linearnih in kotnih kinematičnih značilnosti

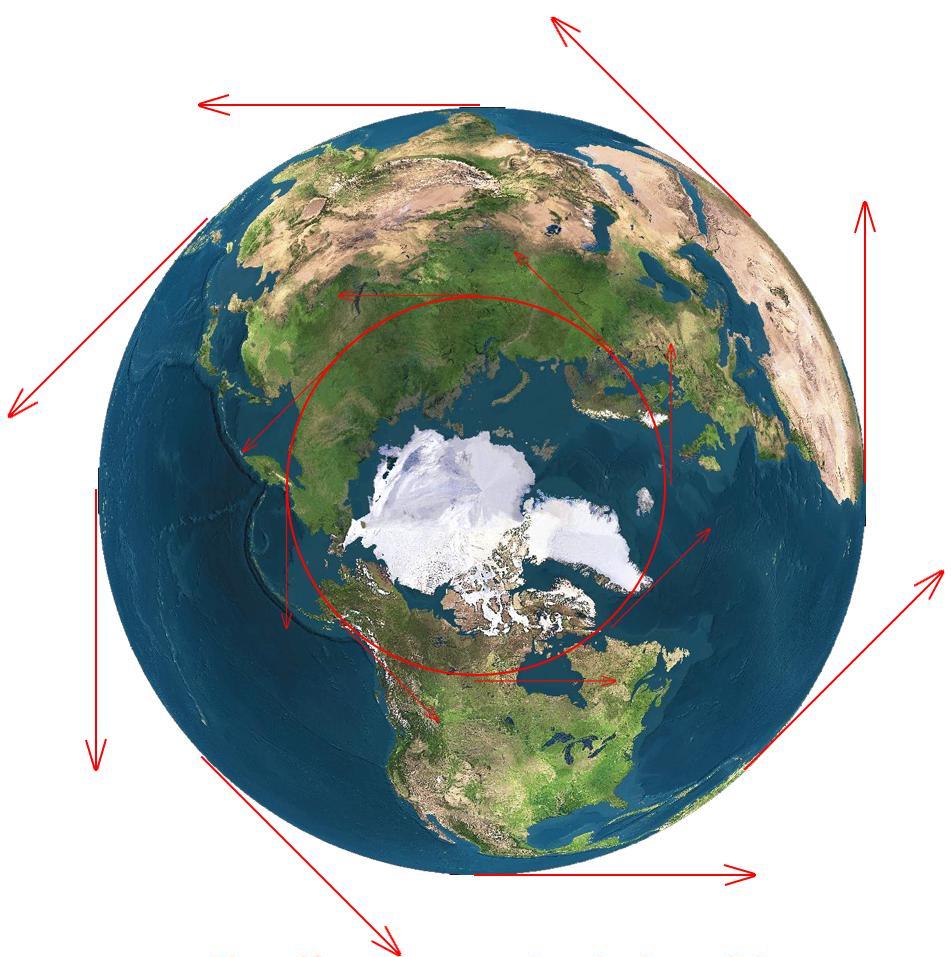
Zgoraj je bila dana formula za centripetalni pospešek, zapisana preko linearne hitrosti v. Vendar pa je ta formula lahko zapisana tudi z ustreznimi kotnimi značilnostmi ω.

Recimo, da je vrteče se telo v času t okrog kroga zavrtelo eno revolucijo. Potem lahko za linearne in kotne hitrosti zapišemo:

v = 2 * pi * r / t;

ω = 2 * pi / t

Od tod je razvidno, da je modul linearne hitrosti v r krat velikost magnitude ω, to je:

v = ω * r

Ta enakost povezuje kotne in linearne hitrosti. Z njo lahko zapišemo formulo za _c skozi ω:

a _c = ω ² * r

Zdaj izračunamo v formuli s hitrostmi časovne izvedenke za levo in desno stran enakosti, dobimo:

dv / dt = dω / dt * r =>

a = α * r

Ta enakost povezuje linearno pospeševanje a, ki je tangencialno usmerjeno na krog in njegov kotni analog α.

Enostavno je dokazati, da je osrednji kot vrtenja θ pri gibanju okoli kroga povezan z dolžino njegovega loka L z naslednjim izrazom:

L = θ * r

Tukaj, če je θ enako 2 * pi radianom (polna revolucija), dobimo dolžino kroga L.

Rešitev problema določanja centripetalne sile

Znano je, da je bil kamen z maso 0,5 kg vezan na 1-metrsko vrv in so jo začeli vrteti s kotno frekvenco 3 vrtljajev na sekundo. Najti morate napetostno silo vrvi F _c .

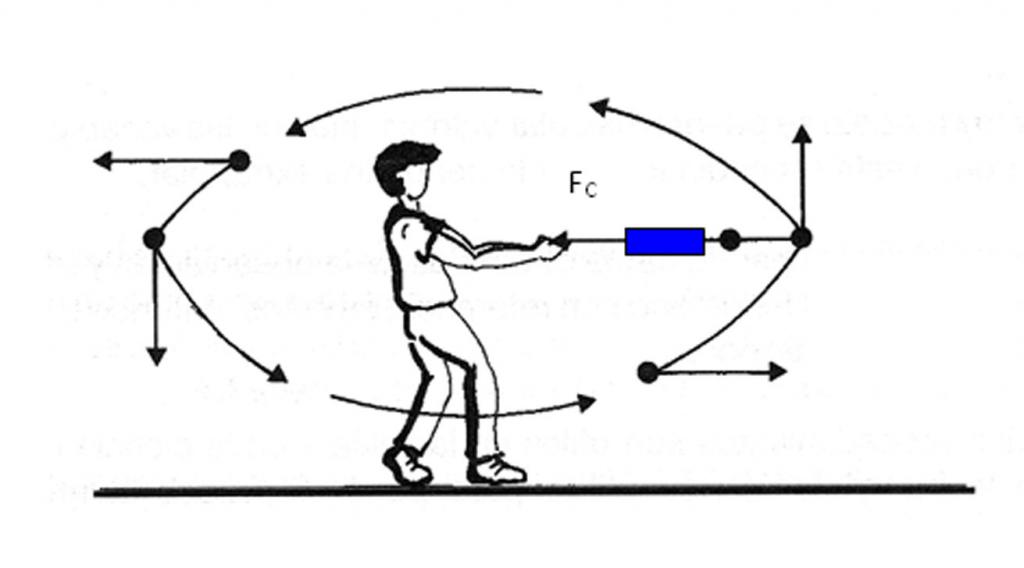
Napetostna sila Fc je centripetalna. Lahko se izračuna po formuli:

F _c = m * a _c

Masa kamna m je znana. Centripetalni pospešek a _c lahko izračunamo iz poznavanja kotne hitrosti ω. S frekvenco f, določeno v nalogi, je količina ω povezana z izrazom:

ω = 2 * pi * f

Potem bo centripetalni pospešek izračunan kot:

a _c = 4 * pi ² * f ² * r

Želena sila F _c bo enaka:

F _c = 4 * pi ² * f ² * r * m

Če je pogoj problema nadomestiti podatke v tej formuli, dobimo vrednost sile F _c , ki je približno enaka 177,5 N.