Kombinatorika - kaj je to? Elementi kombinatorike
Specialisti na različnih področjih morajo reševati kombinacijske probleme: preureditev števil, znakov in drugih predmetov. Na primer, vodja trgovine mora razdeliti različne vrste dela med delovnimi stroji. Kombinatorika je pomembna veja matematike, ki, kot je težko uganiti, najde svojo nišo na različnih področjih in specialnostih: fizika, biologija, jezikoslovje, kemija, inženiring, teorija kodiranja in še veliko več. Načela kombinatorike so tudi osnova rešitve verjetnostnih problemov.
Zgodovina
Prvi predpogoji kombinatorike kot znanosti so se pojavili v 16. stoletju. Prispevala k razvoju tega področja znanja v veliki meri, fascinacija ljudi z igrami na srečo: kartice, kocke, loterija izgubil ne le zlato in dragulje, ampak palače in posesti. Zato se sprašujete, na primer, kako pogosto lahko na kosti dobite dober nabor točk ali dobite dva asa. Ljudje so postopoma prišli do osnov kombinatorike in verjetnosti. Ali so kombinatoriki pomagali nekemu zmagati ali izgubiti manj? Vprašanje je zanimivo, vendar je njegova obravnava izven obsega tega člena.

Prvi matematik, ki se je aktivno ukvarjal s kombinatoriko, je bil italijanski italijanski Tartaglia (1499-1557), po katerem so se taki ugledni znanstveniki, kot sta Pascal, Fermat, Bernoulli, Leibnitz, Euler in drugi, aktivno ukvarjali s proučevanjem teh vprašanj. še vedno je ostala, če ne zabavna igra s številkami, potem pa teorija, ki se uporablja izključno v igrah na srečo in nima pravice uporabljati drugje.
Razvoj kombinatorike
Pomemben napredek v kombinatoriki se je zgodil s prihodom 20. stoletja. računalniki, programiranje in kar je najpomembnejše - diskretna matematika. V tem obdobju kombinatorika doseže vrh svojega hitrega razvoja in postane polnopravna znanost. Kombinatorne metode se začnejo uporabljati povsod:
- reševanje prometnih problemov;
- razporejanje;
- Priprava načrtov za proizvodnjo in prodajo blaga;
- v teoriji naključnih procesov;
- matematična statistika in teorija verjetnosti;
- pri pripravi in izvedbi poskusov;
- v šahu;
- v termodinamiki;
- v geometriji;
- in na mnogih drugih področjih.
Vraževerni izziv
Na svetu je bil vodja, ki je verjel, da mu številka 8 prinaša popolne neuspehe. Zato se je odločil, da se bo znebil vseh številk, ki bodo vsebovale osem številk. Pod njegovim nadzorom je delalo 600 ljudi. Vsi so imeli identifikacijsko številko vozovnica za delo, sestavljena iz treh številk. Ne da bi dvakrat premišljeval, se je vodja odločil, da iz števila prelazov izključi številko 8. In potem se je spraševal, če je bilo na voljo 600 različnih oseb, ki so se gibale v razponu od 000 do 999, kar ne bi vključevalo 8?
Očitna rešitev tega problema je ročno odpisovanje vseh številk od 000 do 999 in prečrtanje tistih, v katerih je osem. Ali je problem mogoče rešiti na enostavnejši način? Če je za 999 številke izvedljiva naloga z oštevilčenjem vseh variant, bo obseg od 000000 do 999999 zahteval veliko več napora. To je, da prihranite čas in napor, zasnovane kombinatorično.
Rešitev problema vraževernega voditelja
Druga rešitev je naslednja. Če izločimo 8 iz serije, dobimo, da so 0, 1, 2, 3, 4, 5, 6, 7, 9 - teh devet številk veljavne. Po tem boste našli vse dvoštevilčne številke, ki ne bodo vsebovale 8. To se naredi preprosto: od veljavnega morate vzeti poljubno število in mu dodati še poljubno število iz veljavnega. Tako bomo zlahka dobili vse dvomestne številke, ki ustrezajo pogoju. Zato dobimo, da bo vsaka posamezna številka dala 9 različnih dvomestnih številk. Skupno število teh številk bo 9 * 9 = 9 2 = 81.
Če nadaljujemo z analogijo, lahko sklepamo, da je za pridobitev vseh trimestnih števil brez osmic potrebno obstoječim dvomestnim številkam dodeliti tudi tretjo številko, tudi iz dovoljenih vrednosti. Potem bomo ugotovili, da bo število takih številk 9 2 * 9 = 9 * 9 * 9 = 729. Tako smo ugotovili, da bi lahko vodja našega vodje z lahkoto zagotovil 600 zaposlenih z vrzelmi, ki ne bi vsebovale 8. Poskusite rešiti problem zase s petmestnimi številkami.
In kaj se bo zgodilo, če menedžerju ni všeč številka 2? Izkazalo se je, da bo število sprejemljivih številk 8, in sicer: 0, 1, 3, 4, 5, 6, 7, 9. Potem, potem ko smo ocenili število kombinacij števil brez 2 in 8, lahko sklepamo, da je njihovo število 8 * 8 * 8 = 512, in to očitno ni dovolj, da bi zagotovilo 600 oseb s prepustnicami. Kombinatorika je znanost, ki pomaga odgovoriti na takšna vprašanja bolj učinkovito kot s silo.
Loto problem
Vsakdo pozna igro. Obstaja vreča, v kateri ležijo sodi s številkami od 1 do 90. Vstopnice so razdeljene vsem udeležencem, v katerih je potrebno preliti določeno število celic s številkami. Nato vodilni loto pride iz vrečke enega od oštevilčenih sodov. Zmagovalec bo tisti, ki je prečrtal večino številk v vozovnici, kar sovpada s tistimi, ki jih je gostitelj igre izvlekel.

Ko je Nina igrala loto, je mislila. Pogosto je gledala, kako voditelj dobi isto številko iz vreče. Hkrati pa sta se prvi dve kegi izkazali za enako manj pogosto. Potem se je spraševala, koliko načinov lahko dosledno dobite dve vreči? Elementi kombinatorike pomagajo odgovoriti na njeno vprašanje.
Loto rešitev
Očitno je, da lahko prvi sod ima številke od 1 do 90. Z drugimi besedami, obstaja 90 načinov za pridobivanje prvega soda. Kaj pa naslednjič? Če je npr. V vrečki odstranjen keg št. 63, se v trenutni igri ne bo več ponovilo.
Metoda tabele nam bo pomagala rešiti problem. V naslovu in naslovu bodo izpisane številke od 1 do 90. Tako bo na presečišču katere koli črte in katerega koli stolpca par številk ali pa bo iz vreče odstranjen par sodov. Hkrati se na diagonali tabele nahajajo isti par številk. Kar je nemogoče glede na stanje, saj je po odstranitvi ene števke iz vrečke njegovo ponavljanje nemogoče. Pridobite tabelo v naslednji obliki:
| 1 | 2 | ... | 90 | |
| 1 | x | 1, 2 | ... | 1, 90 |
| 2 | 2, 1 | x | ... | 2, 90 |
| ... | ... | ... | x | ... |
| 90 | 90, 1 | 90, 2 | ... | x |
Skupaj dobimo tabelo, v kateri je število celic 90 * 90 = 8100. Ne smemo pozabiti, da obstaja 90 parov številk, ki so diagonalno nameščene in so nemogoče glede na pogoje. Potem bo odgovor na vprašanje, koliko načinov lahko dobite 2 vreči iz vrečke, 8100 - 90 = 8010 možnosti.
Na drugačen način lahko dosežete enak odgovor. Za prvi sod je 90 možnosti. Po prvem izvleku ostane 89 možnosti za drugi sod. Tako bo skupno število možnosti 90 * 89 = 8010. Elemente kombinatorike lahko uporabimo na različne načine. Edino vprašanje je enostavnost in univerzalnost metode. Na primer, metoda tabele se lahko uporabi za tri sode, ki jih je treba izvleči zaporedoma, in to bo očitno meja. In kaj za štiri ali več?
Problem s posadko
Če so izbire odvisne od tega, kateri predmeti so bili prej izbrani, je primerno, da se tak postopek prikaže kot "drevo". V prvem koraku je toliko točk postavljenih iz ene točke, kot je mogoče v prvi fazi. Na koncu vsake vrstice je tudi toliko dodatnih vrstic, kot je mogoče narediti v drugem koraku, itd. Posledično bo narisana vrsta drevesa ali grafa. Kombinatorika in teorija lahko zvenijo precej zmedeno in nerazumljivo, zato poglejmo primer.
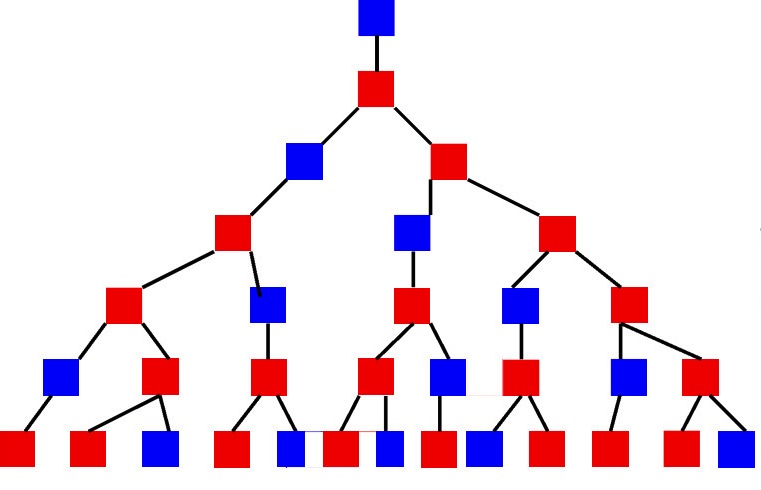
Pred začetkom ekspedicijskega leta ima vodstvo nalogo - zbrati posadke za potovanja. Vsaka ekipa mora imeti tri osebe: poveljnika, inženirja in zdravnika. Hkrati se lahko število strokovnjakov na določenem področju razlikuje. Dovoljeno je, na primer, da se en zdravnik pošlje v dve različni odpravi, saj sta le dva zdravnika, v vsakem poveljniku in inženirju je lahko tri. V tem primeru mora pripravljavec ekspedicijskega načrta upoštevati psihološko združljivost članov ekipe. Ta značilnost je ena izmed najpomembnejših v dolgih in daljnih odpravah za njihovo uspešno ravnanje. Na podlagi vseh opisanih pogojev se pojavi naslednja slika:
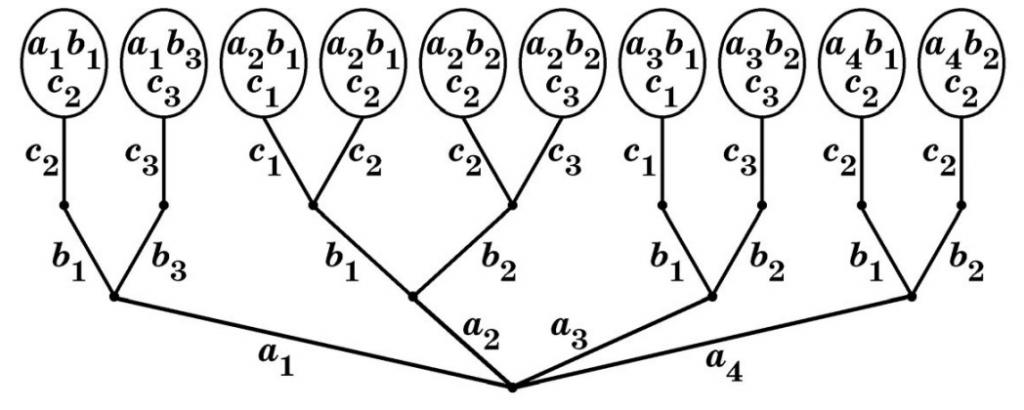
Kjer sem i, so poveljniki, b i so inženirji in c i so zdravniki. Hkrati je bilo med preizkušanjem vsake osebe ugotovljeno, da se poveljnik a 1 psihološko dobro ujema z inženirji b 1 in b 3 , a 2 - z b 1 in b 2 , vendar je zdravnik c 3 nezdružljiv z inženirjem b 1 , itd. Vprašanje, ki je bilo prvotno postavljeno vodji projekta, je bilo, koliko posadk je mogoče sestaviti pod takimi pogoji. Iz grafikona je razvidno, da je skupaj 10 takih posadk, toda kaj bi se zgodilo, če vprašanje psihološke združljivosti ne bi imelo teže? Potem se izkaže, da bi po izbiri poveljnikov a i obstajale tri alternative za vsakega izmed njih pri izbiri inženirja. Zato bi za par poveljnika in inženirja obstajale tudi tri možnosti za zdravnike. Potem bo število kombinacij doseglo 4 * 3 * 3 = 36 posadk.
Umestitve, permutacije in kombinacije
V zgornjih primerih je rešitev problemov nastala s tako imenovano aksiomatsko metodo. To pomeni, da lahko rečemo, da obstajajo številne osnovne naloge, katerih reševanje je mogoče zmanjšati na številne probleme. Vendar, tako kot pri stereometriji, je neprimerno reševati probleme, ki temeljijo izključno na aksiomih, za to pa se uporablja bolj priročno orodje, imenovano »izreki«, zato je v kombinatoriki bolj priročno uporabljati bolj posplošene in preizkušene metode. Med večstoletno študijo kombinatorike je postalo očitno, da se številne naloge srečujejo pogosteje kot druge, ločile so se v ločene razrede in dobile imena, ki so postale glavna kombinatorika, namreč umestitve, permutacije in kombinacije.

Kombinatorni problemi
Eden od ključnih problemov kombinatornih metod je določiti, kateri sklop nalog je treba obravnavati kombinatorno. Tega ne moremo strogo določiti zaradi izredno široke palete problemov, ki spadajo v kombinatorno kategorijo. In potem se lahko mnoge naloge nanašajo na kombinatoriko, pa tudi na drugo področje, ki je sosednje ali mejno.

V poenostavljenem primeru je mogoče ugotoviti, da kombinatorna matematika vključuje probleme, ki vključujejo vzorce in lokacije objektov. Hkrati pa je za kombinatoriko značilno delo izključno s končnim nizom objektov. Na podlagi teh določb lahko ločimo naslednje naloge, značilne za kombinatoriko:
- Naredite izbor predmetov ob upoštevanju vseh lastnosti.
- Dokazati ali ovreči obstoj vzorca pod določenimi pogoji.
- Poiščite število možnih kombinacij.
- Poiščite vse kombinacije in določite algoritem za njihovo štetje.
- Poiščite optimalno rešitev problema pod danimi pogoji.
Če je problem mogoče dodeliti enemu od teh tipov, potem je kombinatorična in kombinatorne formule pomagajo pri njenem reševanju.