Osnovni pojmi teorije verjetnosti in matematične statistike

Matematika vključuje celoten sklop področij, od katerih je ena, skupaj z algebro in geometrijo, teorija verjetnosti. Obstajajo izrazi, ki so skupni vsem tem področjem, poleg njih pa obstajajo specifični, posebni le eni posamezni "nišni" besedi, formule, izreki.

Izraz »teorija verjetnosti« povzroča paniko v nepripravljenem učencu. Dejansko domišljija barve slike, kjer se pojavijo grozne volumetrične formule, in rešitev enega problema zavzame celoten zvezek. Vendar pa v praksi stvari sploh niso tako strašne: dovolj je, da enkrat razumemo pomen nekaterih izrazov in pridemo do jedra neke posebne logike razmišljanja, da bi se enkrat za vselej prenehal bati nalog. Pri tem upoštevamo osnovne pojme teorije verjetnosti in matematične statistike - mlado, a izredno zanimivo področje znanja.

Zakaj učiti koncepte

Funkcija jezika je, da posreduje informacije od ene osebe do druge, tako da jo razume, jo uresniči in jo lahko uporabi. Vsak matematični koncept je mogoče razložiti s preprostimi besedami, vendar bi v tem primeru za izmenjavo podatkov potrebovali veliko več časa. Predstavljajte si, da bi namesto besede "hipotenuza" vedno morali reči "najdaljša stran pravokotnega trikotnika" - to je zelo neprijetno in dolgo.

Zato ljudje izumljajo nove izraze za določene pojave in procese. Na enak način so se pojavili osnovni pojmi teorije verjetnosti - dogodek, verjetnost dogodka itd. Zato, da bi uporabili formule, rešili probleme in uporabili veščine v življenju, je potrebno ne le zapomniti nove besede, ampak tudi razumeti, kaj pomeni vsako od njih. Bolj ko se jih globoko zavedate, se poglobite v pomen, širši je obseg vaših možnosti in bolj popolno zaznavate svet okoli sebe.

Kakšen je smisel subjekta

Spoznajmo se z osnovnimi pojmi teorije verjetnosti. Klasična definicija verjetnosti je naslednja: to je razmerje med rezultati, ki ustrezajo raziskovalcu in skupnemu številu možnih. Dajmo preprost primer: ko oseba zavrti kocko, lahko spusti katerokoli od šestih strani navzgor. Tako je skupno število rezultatov šest. Verjetnost naključno izbranega padca je 1/6.

Sposobnost napovedovanja nastanka določenega rezultata je izjemno pomembna za različne strokovnjake. Koliko okvarjenih delov se pričakuje veliko? Odvisno je od tega, koliko proizvajati. Kakšna je verjetnost, da bo zdravilo pomagalo pri boju proti bolezni? Takšne informacije so bistvenega pomena. Toda ne izgubljajmo časa na dodatnih primerih in nadaljujemo s preučevanjem novega področja za nas.

Prva poznanica

Razmislite o osnovnih pojmih teorije verjetnosti in njihovi uporabi. V naravnost Znanosti, ekonomske formule in izrazi, ki so predstavljeni spodaj, se uporabljajo povsod, saj so neposredno povezani s statistiko in napakami pri meritvah. Podrobnejša študija tega vprašanja vam bo odprla nove formule, ki so uporabne za natančnejše in bolj zapletene izračune, a začnimo s preprostim.

Eden najbolj osnovnih in osnovnih konceptov teorije verjetnosti in matematične statistike je naključen dogodek. Pojasnite z jasnimi besedami: od vseh možnih izidov poskusa se kot rezultat opazi le ena. Tudi če je verjetnost pojava tega dogodka precej višja od druge, bo to naključno, saj bi bil teoretično lahko rezultat drugačen.

Če smo izvedli serijo poskusov in pridobili določeno število rezultatov, potem se verjetnost vsakega od njih izračuna po formuli: P (A) = m / n. Tu je m, kolikokrat smo v testnih serijah videli rezultate, ki nas zanimajo. Po drugi strani pa je n skupno število izvedenih poskusov. Če smo 10-krat vrgli kovanec in 5-krat dobili "rep", potem je m = 5 in n = 10.

Vrste dogodkov

Zgodi se, da je v vsakem poskusu zagotovljen določen izid - tak dogodek se bo imenoval zanesljiv. Če se nikoli ne zgodi, se bo imenovala nemogoča. Vendar pa se taki dogodki ne uporabljajo v pogojih problemov v teoriji verjetnosti. Osnovni pojmi, ki so veliko pomembnejši, so skupni in nezdružljivi dogodki.

Zgodi se, da se med poskusom pojavita dve dogodki hkrati. Na primer, zavijemo dve kocki - v tem primeru dejstvo, da je nekdo imel »šest«, ne zagotavlja, da drugi ne bo padel na drugo. Takšni dogodki se bodo imenovali skupni.

Če umaknemo eno, potem dve številki hkrati ne bosta mogli izpasti. V tem primeru se izidi v obliki padajočega „enega“, „dva“ itd. Obravnavajo kot nezdružljivi dogodki. Zelo pomembno je razlikovati med rezultati, ki se pojavijo v vsakem posameznem primeru - odvisno od tega, katere formule naj uporabimo pri iskanju verjetnosti. Temeljne koncepte teorije verjetnosti bomo nadaljevali v naslednjih odstavkih, ko bomo upoštevali značilnosti seštevanja in množenja. Brez njih ni mogoče rešiti nobenega problema.

Količina in izdelek

Recimo, da umreš s prijateljem, in ima »štiri«. Za zmago moraš dobiti pet ali šest. V tem primeru se verjetnosti seštevajo: ker sta verjetnost padca obeh številk 1/6, bo odgovor izgledal kot 1/6 + 1/6 = 1/3.

Sedaj si zamislite, da dvakrat zavrtite kocko, in vaš prijatelj je dobil 11 točk. Sedaj morate imeti »šest« dvakrat zapored. Dogodki so neodvisni drug od drugega, zato je treba verjetnost pomnožiti: 1/6 * 1/6 = 1/36.

Med osnovnimi pojmi in izreki teorije verjetnosti je treba paziti na vsoto verjetnosti skupnih dogodkov, t. to so tiste, ki se lahko pojavijo hkrati. Formula dodatka v tem primeru bo izgledala takole: P (A + B) = P (A) + P (B) - P (AB).

Kombinatorika

Zelo pogosto moramo poiskati vse možne kombinacije nekaterih parametrov objekta ali izračunati število kakršnih koli kombinacij (npr. Pri izbiri šifre). Pri tem nam bo pomagala kombinatorika, ki je tesno povezana s teorijo verjetnosti. Osnovni pojmi tukaj vsebujejo nekaj novih besed, številne formule iz te teme pa bodo zagotovo koristne.

Recimo, da imate tri številke: 1, 2, 3. Če jih želite uporabiti, lahko zapišete vse možne trimestne številke. Koliko jih bo? Odgovor: n! (klicaj. t pomeni faktorsko). Kombinacije številnih različnih elementov (številke, črke itd.), Ki se razlikujejo le po vrstnem redu njihove lokacije, se imenujejo permutacije.

Vendar pa pogosteje naletimo na takšno situacijo: obstaja 10 mest (od nič do devet), od katerih je sestavljeno geslo ali koda. Recimo, da je dolžina 4 znakov. Kako izračunati skupno število možnih kod? Za to obstaja posebna formula: (n!) / (N - m)!

Glede na zgornji predlagani problemski pogoj n = 10, m = 4. Poleg tega so potrebni samo preprosti matematični izračuni. Mimogrede, takšne kombinacije se bodo imenovale umestitev.

Končno obstaja koncept kombinacij - to so zaporedja, ki se med seboj razlikujejo z vsaj enim elementom. Njihovo število se izračuna po formuli: (n!) / (M! (Nm)!).

Matematično pričakovanje

Pomemben koncept, s katerim se študent srečuje že v prvih razredih na tem področju, je matematično pričakovanje. To je vsota vseh možnih rezultatov, pomnoženih z njihovimi verjetnostmi. V bistvu je to povprečno število, ki ga lahko predvidimo kot rezultat testa. Na primer, obstajajo tri vrednosti, za katere so verjetnosti prikazane v oklepajih: 0 (0,2); 1 (0,5); 2 (0,3). Izračunaj pričakovanje: M (X) = 0 * 0.2 + 1 * 0.5 + 2 * 0.3 = 1.1. Tako iz predlaganega izraza vidimo, da je ta vrednost konstantna in ni odvisna od izida testa.

Ta pojem se uporablja v mnogih formulah in v prihodnosti ga boste večkrat naleteli. Z njim je enostavno delati: pričakovanje vsote je enako vsoti mat. pričakovanja - M (X + Y) = M (X) + M (Y). Enako velja za izdelek: M (XY) = M (X) * M (Y).

Disperzija

To mora biti iz tečaja fizične šole, ki se ga spomnite, da se razpršitev razprši. Kakšno je njegovo mesto med osnovnimi pojmi teorije verjetnosti?

Poglejte dva primera. V enem primeru smo dobili: 10 (0,2); 20 (0,6); 30 (0,2). V drugi - 0 (0,2); 20 (0,6); 40 (0,2). Matematično pričakovanje v obeh primerih bo enako, kako lahko primerjamo te situacije? Navsezadnje s prostim očesom vidimo, da je širjenje vrednosti v drugem primeru veliko večje.

Za to je bil uveden koncept disperzije. Da bi ga dobili, morate izračunati pričakovanje vsote razlik vsake naključne spremenljivke in pričakovanja. Vzemite številke iz prvega primera, zabeleženega v prejšnjem odstavku.

Najprej izračunamo pričakovanje: M (X) = 10 * 0,2 + 20 * 0,6 + 30 * 0,2 = 20. Nato vrednost variance: D (X) = 40.

Drugi temeljni koncept statistike in teorija verjetnosti je standardni odklon. Izračunajte, da je zelo preprosta: morate samo vzeti kvadratni koren iz disperzije.

Tu lahko opazimo tako preprost izraz, kot področje. Ta vrednost kaže razliko med najvišjo in najnižjo vrednostjo v vzorcu.

Statistika

Nekateri osnovni šolski koncepti se v znanosti uporabljajo zelo pogosto. Dva izmed njih sta aritmetična sredina in mediana. Seveda se spomnite, kako najti njihove vrednote. Ampak za vsak primer, se spomnimo: aritmetično povprečje je vsota vseh vrednosti, deljeno s številom. Če je vrednost 10, jih dodamo in razdelimo za 10.

Sredina je osrednjega pomena za vse možne. Če imamo liho število vrednosti, jih zapišemo v naraščajočem vrstnem redu in izberemo tisto, ki je bila v sredini. Če imamo celo število vrednot, vzamemo dve osrednji in delimo na dve.

Še dve vrednosti, ki se nahajata med mediano in dvema skrajnima vrednostma največje in najmanjše vrednosti, se imenujejo kvartili. Izračunajo se na enak način - z neparnim številom elementov se vzame število, ki se nahaja sredi vrstice, za celo - polovico vsote dveh osrednjih elementov.

Obstaja tudi poseben graf, v katerem so prikazane vse vrednosti vzorca, njegov obseg, mediana, interval četrtletja, pa tudi outliers - vrednosti, ki se ne uvrščajo v statistično napako. Nastala slika ima zelo specifično (in celo ne-matematično) ime - škatlo z brki.

Distribucija

Distribucija se nanaša tudi na osnovne pojme teorije verjetnosti in matematične statistike. Skratka, gre za povzetek vseh naključnih spremenljivk, ki jih lahko vidimo kot rezultat testa. Glavni parameter tukaj je verjetnost pojava vsake posamezne vrednosti.

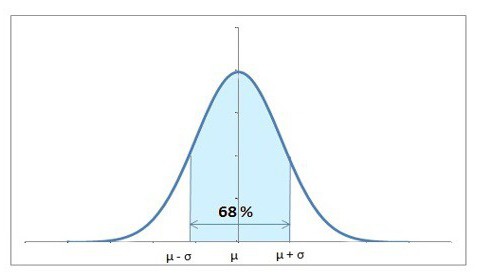Normalna porazdelitev je tista, ki ima en osrednji vrh, v katerem se nahaja največja vrednost. Iz nje se razslojujejo vedno manj verjetni izidi. Na splošno je razpored s strani videti kot »slide«. V prihodnosti se boste naučili, da je osrednji mejni izrek, ki je temelj za teorijo verjetnosti, tesno povezan s to vrsto porazdelitve. Opisuje zakone, ki so pomembni za veje matematike, ki jih obravnavamo, in ki so zelo koristne za različne izračune.

Toda nazaj na temo. Obstajata še dve vrsti porazdelitev: asimetrična in multimodalna. Prvi je videti kot polovica "normalnega" grafa, tj. Lok se spušča le v eni smeri od najvišje vrednosti. Končno, multimodalna porazdelitev je tista, ki ima več »zgornjih« vrednosti. Torej razpored pade, nato se dvigne. Največja frekvenčna vrednost v kateri koli distribuciji se imenuje način. Je tudi eden od osnovnih pojmov teorije verjetnosti in matematične statistike.

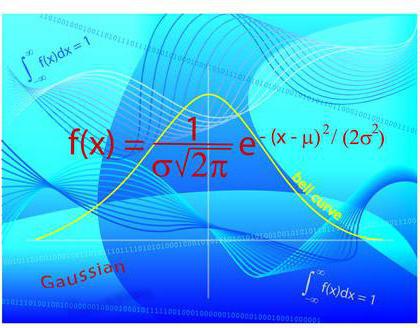
Gaussova porazdelitev

Gaussova ali normalna porazdelitev je tista, v kateri odstopanje opazovanj od povprečja spoštuje določen zakon.

Skratka, glavna razpršenost vzorčnih vrednosti eksponentno teži k načinu - najpogostejši izmed njih. Če govorimo natančneje, potem je 99,6% vseh vrednosti znotraj treh standardnih odstopanj (spomnite se, da smo pogledali ta koncept zgoraj?).

Gaussova porazdelitev je eden od osnovnih pojmov teorije verjetnosti. S pomočjo tega je mogoče razumeti, ali je element vključen v kategorijo »tipičnega« po enem ali drugem parametru - to je, kako se višina in teža osebe ocenjujeta glede na starost, stopnjo intelektualnega razvoja, psihološko stanje in še veliko več.

Kako se prijaviti?

Zanimivo je, da lahko »dolgočasne« podatke iz matematike uporabite v vašo korist. Na primer, en mladenič je uporabil teorijo verjetnosti in statistiko za pridobitev več milijonov dolarjev v ruleti. Res je bilo, da smo se morali za to pripraviti - v nekaj mesecih smo zabeležili rezultate iger v različnih igralnicah.

Po analizi je ugotovil, da je ena izmed tabel nekoliko nagnjena, kar pomeni, da se številne vrednosti pojavijo statistično značilno pogosteje kot druge. Malo izračuna, potrpežljivost - in zdaj lastniki institucije so zmedeni, razmišljanje, kako lahko oseba dobil tako srečo.

Obstaja veliko vsakodnevnih vsakodnevnih nalog, ki jih ni mogoče rešiti brez uporabe statistike. Na primer, kako določiti, koliko trgovina za naročanje oblačil različnih velikosti: S, M, L, XL? Da bi to naredili, je treba analizirati, kdo pogosto kupuje oblačila v mestu, na območju, v bližnjih trgovinah. Če takšne informacije ne dobijo, lastnik tvega, da bo izgubil veliko denarja.

Zaključek

Obravnavali smo celo vrsto osnovnih pojmov teorije verjetnosti: test, dogodek, permutacije in umestitve, pričakovanje in varianco, način in normalno porazdelitev ... Poleg tega smo preučili številne formule, ki so bile namenjene študiju več kot enomesečnega študija.

Ne pozabite: matematika je potrebna pri študiju ekonomije, naravoslovja, informacijske tehnologije, inženirskih specialitet. Tudi statistikam kot enemu od svojih področij tukaj ni mogoče preprečiti.

Zdaj je na vas: praksa, reševanje problemov in primeri. Tudi temeljni pojmi in definicije teorije verjetnosti bodo pozabljeni, če ne čas za ponavljanje. Poleg tega se naslednje formule v veliki meri zanašajo na tiste, ki smo jih obravnavali. Zato jih poskušajte zapomniti, še posebej ker jih ni tako veliko.