Aritmetično napredovanje - numerično zaporedje

Nekdo je previden glede besede »napredovanje« kot zelo zapleten izraz iz razdelkov višje matematike. Medtem pa je najpreprostejša aritmetična progresija delo števca taksijev (kjer so še vedno). Razumeti bistvo (in v matematiki ni nič bolj pomembno kot »razumeti bistvo«) aritmetičnega zaporedja ni tako težko, če razumemo več osnovnih pojmov.

Matematična zaporedja številk

Številčno zaporedje običajno imenujemo niz številk, od katerih ima vsaka svojo številko.

in ₁ - prvi član zaporedja;

in ₂ - drugi član zaporedja;

...

in ₇ - sedmi član zaporedja;

...

in _n je n-ti član zaporedja;

Vendar nas ne zanima noben poljuben niz številk in številk. Naša pozornost bo usmerjena na numerično zaporedje, v katerem je vrednost n-tega izraza povezana z njegovim ordinalnim številom z razmerjem, ki ga je mogoče matematično jasno navesti. Z drugimi besedami: numerična vrednost n-te številke je funkcija n.

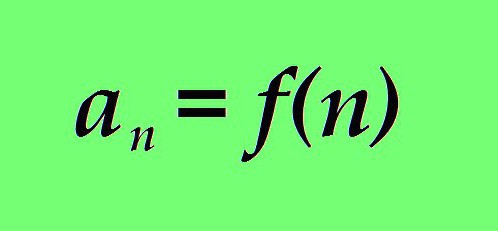
kjer:

a je vrednost člana numeričnega zaporedja;

n je njena zaporedna številka;

f (n) je funkcija, kjer je zaporedna številka v numeričnem zaporedju n argument.

Opredelitev

Aritmetično napredovanje se imenuje numerično zaporedje, v katerem je vsak naslednji mandat več (manj) kot prejšnji z istim številom. Formula za n-ti člen aritmetičnega zaporedja je naslednja:

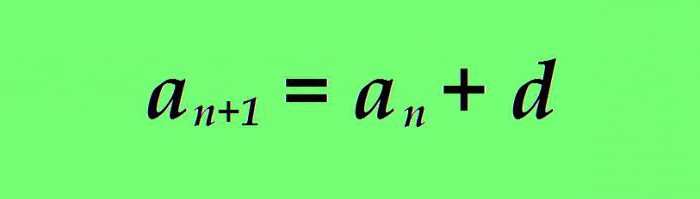
kjer

a _n - vrednost trenutnega člana aritmetičnega napredovanja;

a _{n + 1} je formula za naslednjo številko;

d - razlika (določeno število).

Enostavno je ugotoviti, da če je razlika pozitivna (d> 0), potem bo vsak naslednji član obravnavanega niza večji od prejšnjega in tako aritmetično napredovanje se bo povečalo.

Primer:

a ₁ = 5

d = 3

potem

V spodnjem grafu ni težko ugotoviti, zakaj se številčno zaporedje imenuje "povečevanje".

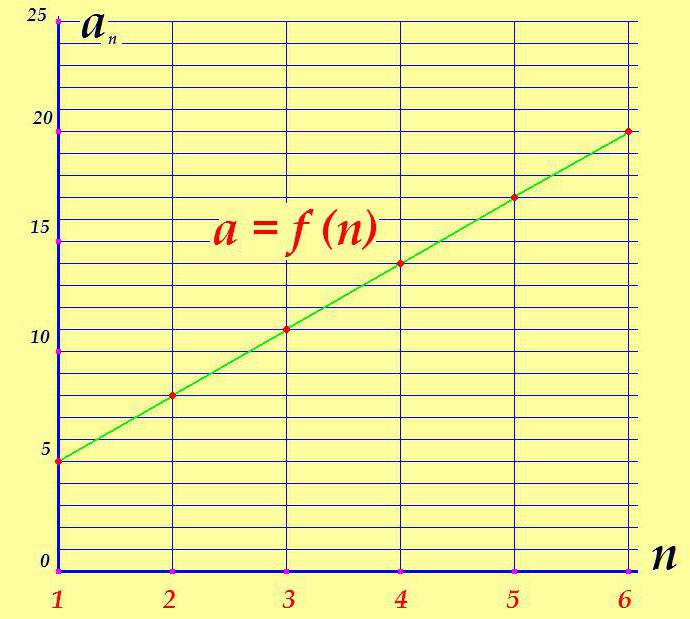
V primerih, ko je razlika negativna (d <0), bo vsak naslednji član iz očitnih razlogov manjši od prejšnjega, grafikon napredovanja pa se bo »spuščal«, aritmetični napredek se bo imenoval padajoči.

Vrednost določenega člana

Včasih je potrebno določiti vrednost poljubnega izraza a _n aritmetične progresije. To lahko naredite tako, da zaporedoma izračunate vrednosti vseh članov aritmetičnega napredovanja od prvega do želenega. Vendar pa taka pot ni vedno sprejemljiva, če je na primer potrebno najti vrednost pettisočinskega ali osemmilijonskega člana. Tradicionalni izračun traja dolgo časa. Vendar pa lahko specifično aritmetično napredovanje raziščemo z uporabo nekaterih formul. Obstaja tudi formula za n-ti mandat: vrednost katerega koli člana aritmetičnega napredovanja se lahko določi kot vsota prvega obdobja napredovanja, pri čemer se razlika napredovanja pomnoži s številom člana, ki ga je treba najti, zmanjšano za eno.

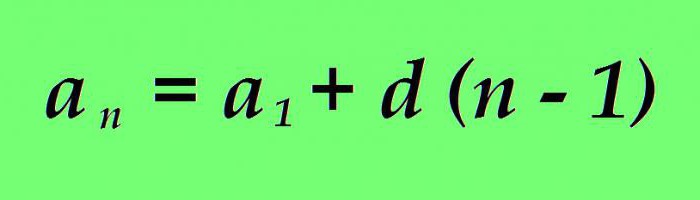
Formula je univerzalna za naraščajoče in padajoče napredovanje.

Primer izračuna vrednosti določenega člana

Rešimo naslednji problem iskanja vrednosti n-tega aritmetičnega napredka.

Pogoj: obstaja aritmetično napredovanje s parametri:

- prvi del zaporedja je 3;

- razlika števila je 1.2.

Naloga: treba je najti vrednost 214 članov

Rešitev: za določitev vrednosti določenega člana uporabimo formulo:

a (n) = a1 + d (n-1)

Če nadomestimo v izrazu podatke iz pogojev problema, imamo:

a (214) = a1 + d (n-1)

a (214) = 3 + 1,2 (214-1) = 258,6

Odgovor: 214. član zaporedja je enak 258,6.

Prednosti te metode izračuna so očitne - celotna rešitev ne obsega več kot 2 vrstici.

Znesek določenega števila članov

Zelo pogosto je v danem aritmetičnem nizu potrebno določiti vsoto vrednosti določenega segmenta. Za to tudi ni treba izračunati vrednosti vsakega člana in nato povzeti. Ta metoda se uporablja, če je število članov, katerih vsota najti, majhno. V drugih primerih je bolj primerno uporabiti naslednjo formulo.

Vsota članov aritmetičnega napredovanja od 1 do n je enaka vsoti prvih in n-ih članov, pomnoženih s številom člana n in razdeljenega na dva dela. Če je v formuli vrednost n-tega člana nadomeščena z izrazom iz prejšnjega odstavka članka, dobimo:

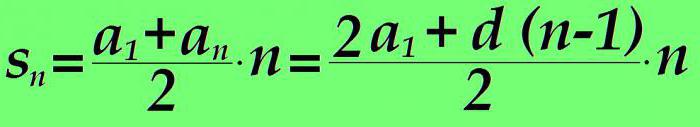
Primer izračuna

Problem rešite na primer z naslednjimi pogoji:

- prvi del zaporedja je nič;

- razlika je 0,5.

Naloga je določiti vsoto članov serije od 56. do 101. leta.

Odločitev. Uporabljamo formulo za določanje količine napredovanja:

s (n) = (2 1 a1 + d ∙ (n-1)) / n / 2

Najprej določimo vsoto vrednosti 101 članov napredovanja, ki v formuli nadomestimo podatke o pogojih naše naloge:

s ₁₀₁ = (2 + 0 + 0,5 ₁₀₁ (101-1)) /2 101/2 = 2 525

Očitno je, da bi ugotovili vsoto članov napredovanja od 56. do 101. točke, je treba odšteti S ₅₅ od S ₁₀₁ .

s ₅₅ = (2 + 0 + 0,5 ₅₅ (55-1)) /2 55/2 = 742,5

Tako je vsota aritmetičnega napredka za ta primer:

s ₁₀₁ - s ₅₅ = 2 525 - 742,5 = 1 782,5

Primer praktične uporabe aritmetičnega napredovanja

Na koncu članka se bomo vrnili na primer aritmetičnega zaporedja, podanega v prvem odstavku - taksimetra (števec avtomobilov taksijev). Razmislite o tem primeru.

Pristanek v taksiju (ki vključuje 3 kilometre) stane 50 rubljev. Vsak naslednji kilometer se plača v višini 22 rubljev / km. Potovanje je oddaljeno 30 km. Izračunajte stroške potovanja.

1. Zavržite prvih 3 km, katerih cena je vključena v stroške pristanka.

30 - 3 = 27 km.

2. Nadaljnji izračun ni nič drugega kot analiza aritmetičnih serij števil.

Številka člana je število prevoženih kilometrov (minus prvih treh).

Članska vrednost je vsota.

Prvi izraz v tem problemu bo enak ₁ = 50 p.

Razlika napredovanja d = 22 str.

število interesov je vrednost (27 + 1) -tega člana aritmetičnega napredovanja - odčitavanje števca na koncu 27. kilometra - 27.999 ... = 28 km.

a ₂₈ = 50 + 22 ∙ (28 - 1) = 644

Formule, ki opisujejo določene numerične sekvence, se uporabljajo za izračun koledarskih podatkov za poljubno dolgo obdobje. V astronomiji je dolžina orbite v geometrijski odvisnosti od razdalje nebesnega telesa do zvezde. Poleg tega se številne numerične serije uspešno uporabljajo v statistiki in drugih uporabnih vejah matematike.

Druga vrsta zaporedja števil je geometrijska.

Za geometrijsko napredovanje je značilna velika, v primerjavi z aritmetično stopnjo spremembe. Ni slučajno, da se v politiki, sociologiji in medicini pogosto reče, da se proces razvija eksponentno, da bi pokazal visoko stopnjo širjenja pojava, na primer bolezni v epidemiji.

N-ti termin geometrijskih številskih vrst se razlikuje od prejšnjega v tem, da se pomnoži s fiksnim številom - imenovalec, na primer, prvi izraz je 1, imenovalec je 2, oziroma:

n = 1: 1 = 2 = 2

n = 2: 2 = 2 = 4

n = 3: 4 = 2 = 8

n = 4: 8 = 2 = 16

n = 5: 16 = 2 = 32,

n = 6: 32 = 2 = 64 in tako naprej ...

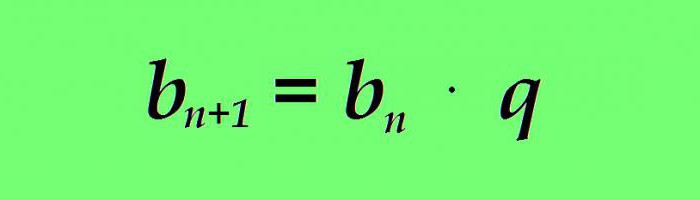
kjer:

b _n - vrednost trenutnega termina geometrijske progresije;

b _{n + 1} - formula za naslednji izraz geometrijske progresije;

q je imenovalec geometrijske progresije (konstantno število).

Če je graf aritmetičnega napredovanja ravna črta, potem geometrična slika nariše nekoliko drugačno sliko:

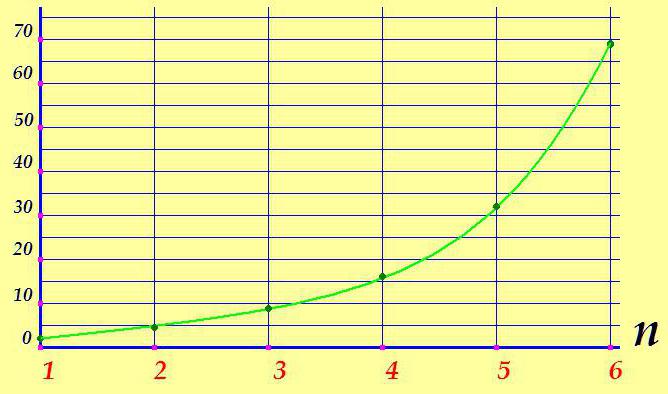
Kot pri aritmetiki ima tudi geometrijska progresija formulo za vrednost poljubnega izraza. Vsak n-ti izraz geometrijske progresije je enak zmnožku prvega izraza po imenovalcu napredovanja v stopnjo n, zmanjšano za eno:

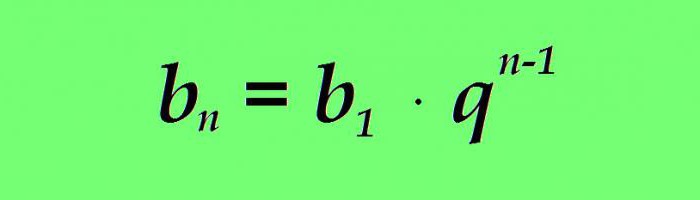
Primer. Imamo geometrijsko napredovanje, pri čemer je prvi izraz enak 3, imenovalec napredovanja pa je enak 1,5. Poiščite 5. člana napredovanja

b ₅ = b ₁ ⁽ q ^(5-1) = 3 ⁴ 1,5 ⁴ = 15,1875

Vsota danega števila članov se izračuna tudi s posebno formulo. Vsota n prvih pogojev geometrijske progresije je enaka razliki produkta n-tega obdobja napredovanja po njenem imenovalcu in prvo obdobje napredovanja, deljeno z imenovalcem, zmanjšano za eno:

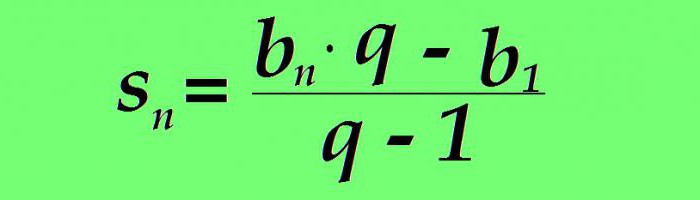
Če se b _n nadomesti z zgornjo formulo, se vrednost vsote n prvih članov obravnavanih serij številk oblikuje:

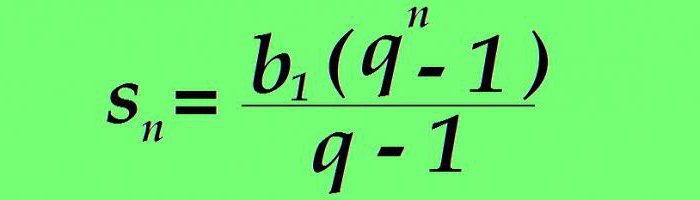
Primer. Geometrijski napredek se začne s prvim izrazom, ki je enak 1. Imenovalec je nastavljen na 3. Poišči vsoto prvih osmih članov.

s8 = 1 ∙ (3 ⁸ -1) / (3-1) = 3 280