Adiabatski proces, njegovo bistvo in formule

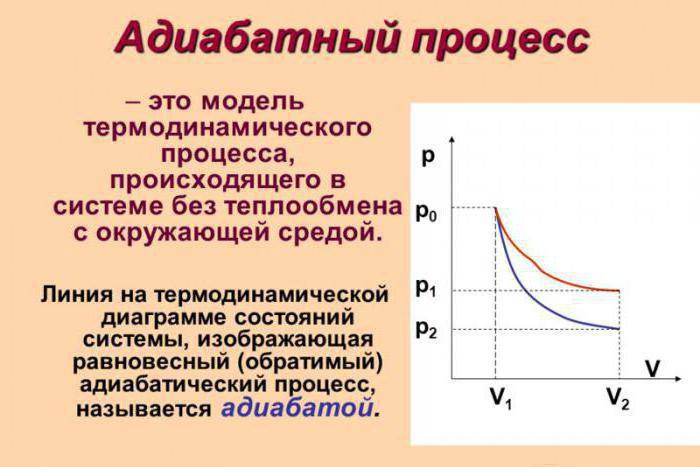
Adiabatski proces (v nekaterih virih imenovan adiabat) je termodinamični proces, ki se odvija v odsotnosti izmenjave toplote z okoljem. Obstaja več dejavnikov, ki označujejo ta razred. Na primer, adiabatski proces se dogaja dinamično in je določen v kratkem času. Obstajajo postopki tega razreda, praviloma, takoj.

Povezava s prvim zakonom termodinamike

Z njim se lahko neposredno poveže adiabatski proces (adiabatski) prvi zakon termodinamike. Besedilo »privzeto« se glasi: sprememba količine toplote v sistemu med termodinamičnim procesom v njej bo numerično enaka vsoti spremembe notranje energije idealnega plina in dela, ki ga opravi ta plin.

Če poskušamo pisati prvi začetek termodinamike v standardni obliki dobimo naslednji izraz: dQ = dU + dA. In zdaj bomo poskušali spremeniti to formulo v povezavi z adiabatnim procesom. Kot smo že omenili, se taki procesi odvijajo pod pogojem, da ni toplotne izmenjave z okolico (zunanje, kot jo imenujejo nekateri literarni viri) medij.

V tem primeru bo formula, ki opisuje prvi zakon termodinamike, dobila naslednjo obliko: dA = -dU. Zdaj pa malo več o spremembah. Če rečemo, da v sistemu ni izmenjave toplote, bo sprememba količine toplote (navedena v formuli prvega zakona termodinamike z dQ) enaka nič. Posledično lahko prenesemo enega od dodatkov z desne na levo, po katerem dobimo formulo, ki smo jo zmanjšali na prej opisano obliko.

Posledica prvega zakona termodinamike za adiabatni proces

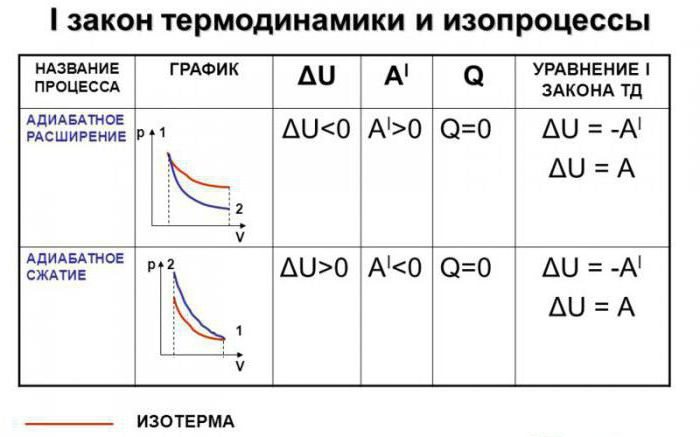
Recimo, da je v sistemu prišlo do adiabatnega procesa. V tem primeru je mogoče, ne da bi se spustili v najmanjše podrobnosti, reči, da plin opravlja delo, medtem ko se širi, hkrati pa izgubi svojo notranjo energijo. Z drugimi besedami, opravljeno delo pri adiabatnem širjenju plina bo izvedeno zaradi izgube notranje energije. Posledično bomo kot rezultat tega procesa upoštevali zmanjšanje temperature same snovi.

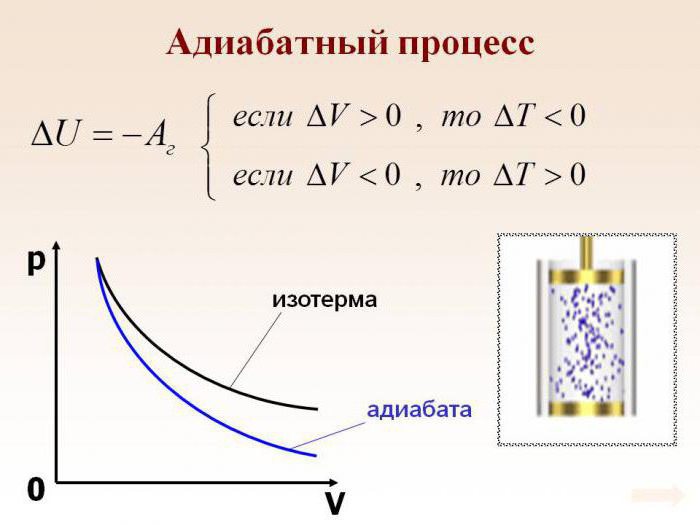
Popolnoma logično je domnevati, da če bo plin adiabatsko stisnjen, se bo njegova temperatura dvignila. Ni težko videti, da se bodo med procesom spremenile vse glavne značilnosti idealnega plina. Gre za njegov pritisk, prostornino in temperaturo. Zato je ime adiabatnega procesa izoprocesa postalo huda napaka.

Adiabatski proces. Formule

Formula, izpeljana iz prvega zakona termodinamike, je bila zapisana prej. Z njim lahko enostavno izračunamo delo na splošno, ki ga bo plin izvajal med adiabatnim procesom. Kot ste morda uganili, bomo to storili s pomočjo integracije.

Da bi dobili splošno formulo za delo za moli plina, integriramo izraz prvega zakona termodinamike za adiabatski proces. Vse to bo izgledalo takole: A = - (integral) dU. Odpremo ta izraz, dobimo: A = - xCv (integral od T1 do T2) dT.

Zdaj, ko smo integrali integral v končno obliko, ga lahko poenostavimo. Na izhodu dobimo naslednjo formulo: A = - xCv (T2 - T1). No, zadnji korak bo manjša poenostavitev. Znebimo se minusa pred formulo. V ta namen naredimo majhno permutacijo v oklepajih, s čimer spreminjamo končno temperaturo z začetnimi mesti. Kot rezultat dobimo: A = xCv (T1 - T2).

Adiabatska enačba

Z uporabo prvega zakona termodinamike za adiabatski proces lahko najdemo adiabatno enačbo. Hkrati pa se beleži za poljubno število molov idealnega plina. Torej, zapišemo prvotno formulo. Izgleda takole: dA + dU = 0. Zelo dobro vemo, da je delo idealnega plina številčno nič več kot produkt spremembe tlaka in volumna.

Hkrati se spremeni notranje energije bo enako delu, opravljenemu z nasprotnim znakom. In že smo jo našli s pomočjo integracije. Zato lahko prvi zakon termodinamike za adiabatni proces ima naslednjo obliko: pdV + xCvdT = 0. Iz te enačbe moramo izključiti en kazalnik, in sicer temperaturo. Namesto tega se spreminja. Pri tem se obračamo na enačbo, ki se pogosto uporablja v molekularni fiziki. Namreč, Mendelejev-Clapeyronova enačba.

Primarni izraz

Razlikovati ga moramo, kar bomo storili. Na splošno je enačba naslednja: PV = XRT. Zaradi razlikovanja se bo zmanjšala na naslednjo obliko: pdV + Vdp = xRdT. Od tu lahko izrazimo spremembo energije. To je enako levemu delu, ki je deljeno z zmnožkom količine snovi in ​​univerzalne plinske konstante. Z drugimi besedami, formula bi bila: (pdV + Vdp) / xR. Ostaja samo poenostavitev. Posledično dobimo naslednji izraz: dT = (pdV + Vdp) / x (Cp - Cv)

Pravzaprav je prvi del naloge zaključen. Ostaja samo, da vse pripelje na misel.

Sekundarni izraz Zamenjava vrednosti

Vzemimo formulo Mendeleev-Clapeyron, ki jo dobimo kot rezultat diferenciacije in jo nadomestimo z izrazom, ki smo ga prej izpeljali za prvi zakon termodinamike glede na adiabatski proces. Torej, kaj dobimo? Vse to okorno izraz ima naslednjo obliko: pdV + xCv ((pdV + Vdp) / x (Cp-Cv)) = 0.

Da bi vse to poenostavili, moramo upoštevati nekaj dejstev. Prvič, izraz lahko poenostavimo tako, da ga zmanjšamo na skupni imenovalec. Ko dobimo eno frakcijo, lahko uporabimo dobro staro pravilo, ki pravi, da je frakcija nič, ko je njen števec nič, in imenovalec je nič. Zaradi kombinacije vseh teh dejanj dobimo naslednji izraz: pCpdV - pCvdV + pCvdV + VCvdp = 0.

Naslednji korak je deliti ta izraz v pVCv. Dobimo vsoto dveh delov, ki daje rezultat nič. To bo Cp / Cv * dV / V + dp / p = 0. Ta formula mora biti integrirana. Potem dobimo naslednji izraz: y (integral) dV / V + (integral) dp / p = (integral) 0.

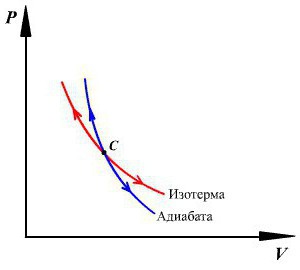
No, potem je vse preprosto. Z integracijskimi formulami (integralne tabele lahko uporabimo za poenostavitev), dobimo naslednji vnos: y ln V + ln p = ln (const). Izkazalo se je, da je p (V) y = const. V molekularni fiziki se ta izraz imenuje Poissonova enačba. Številni znanstveni viri pravijo to formulo tudi za adiabatsko enačbo. Hkrati se vrednost y, ki se pojavi v tem zapisu, imenuje adiabatski indeks. Je enaka (i + 2) / i. Opozoriti je treba, da je adiabatski indeks vedno večji od enega, kar je načeloma logično.

Primeri adiabatnih procesov

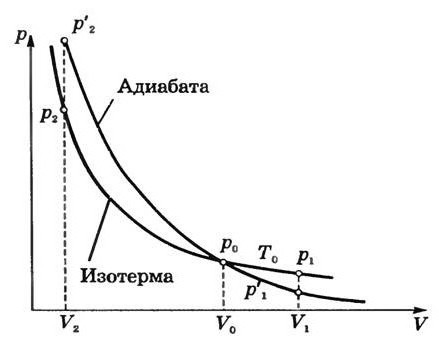
Kmalu po odkritju adiabatnega procesa se je začelo veliko število različnih študij. Tako je nastal prvi teoretični model, ki je povezan s Carnotovim ciklom. Ona je dovolila vzpostavitev pogojnih omejitev, ki so omejevale razvoj toplotnih motorjev. Toda v primeru nekaterih resničnih procesov, ki jih je treba izvesti Carnotov cikel dovolj težko. Stvar je v tem, da je sestavljena iz izoterm. In zahtevajo določitev določene stopnje termodinamičnih procesov.

Zaključek

Da bi se izognili takšnim težavam, je bil izumljen Ottov cikel in cikel utekočinjanje plina. Postali so široko uporabljeni pri reševanju konkretnih problemov v praksi. Začetne študije so pokazale možnost opisovanja nekaterih naravnih procesov v adiabatni ravnini, kar je omogočilo identifikacijo splošnih vzorcev ustreznih procesov. Primer adiabatnega procesa lahko imenujemo kemijska reakcija, ki se pojavi znotraj določene količine plina, če je sistem zaprt in ni izmenjave toplote z zunanjim okoljem.