Pospeševanje gravitacije: odkritje, vzroki, formula

Pospeševanje prostega padca je eno od mnogih odkritij velikega Newtona, ki je ne samo povzel izkušnje svojih predhodnikov, ampak tudi strogo matematično razlago ogromnega števila dejstev in eksperimentalnih podatkov.

Predpogoji za odkritje. Galilejski poskusi

Eden od mnogih poskusov Galileja Galileja je bil posvečen proučevanju gibanja teles v letu. Pred tem je v svetovnem sistemu prevladalo mnenje, da lažja telesa padajo počasneje kot težka. Vrzi različne predmete z višine Poševni stolp, Galileo je ugotovil, da je pospešek prostega padca za telesa z različno maso popolnoma enak. Galileo je upravičeno pripisal majhne razlike med teorijo in eksperimentalnimi podatki vplivu zračnega upora. Da bi dokazal svoje razmišljanje, je predlagal, da se poskus ponovi v vakuumu, toda takrat za to ni bilo tehnične možnosti. Šele mnogo let kasneje je miselni poskus Galilea Isaac Newton.

Newtonova teorija

Čast odkritja pravo sveta pripada Newtonu, toda ideja je bila v zraku že okoli 200 let. Glavni predpogoj za oblikovanje novih načel nebesne mehanike je postal Keplerjev zakon, ki ga je oblikoval na podlagi dolgoletnih opazovanj. Newton je iz morja predpostavk in domnev iznašel predpostavko o sili gravitacije Sonca in razširil svojo teorijo na koncept širine sveta. Preizkusil je svojo hipotezo o inverzni sorazmernosti sile s kvadratom razdalje, pri čemer je upošteval orbito lune. Nadaljnje preizkuse te ideje smo izvedli s študijo gibanja satelitov Jupitra. Rezultati opazovanj so pokazali, da enake sile delujejo med sateliti planetov in planeti, kot v interakciji Sonca in planetov.

Odkritje gravitacijske komponente

Sila gravitacije Zemlje na Sonce je sledila formuli:

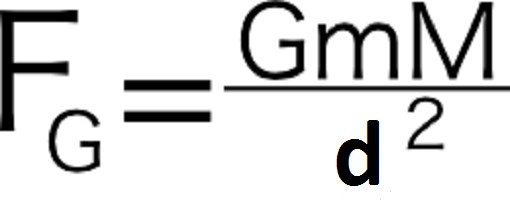
Poskusi so pokazali, da je faktor 1 / d ² v tem razmerju je bilo povsem uporabno v primeru upoštevanja drugih planetov v sončnem sistemu. Konstanta G je bil koeficient, ki je prinesel vrednost deleža v numerično vrednost.

Po svoji teoriji je Newton izmeril masne deleže različnih nebesnih teles, kot je Jupitrova masa / masa Sonca, masa Mesec / masa Zemlje, vendar Newton ni mogel dati numeričnega odgovora na vprašanje, kako velika je teža Zemlje, ker je konstanta G ostala. neznano.

Magnituda gravitacijska konstanta je bila odkrita le pol stoletja po smrti Newtona. Ocene te vrednosti na podlagi hipotez, podobno kot Newtonove predpostavke, so pokazale, da je ta vrednost zanemarljiva in je skoraj nemogoče izračunati njeno vrednost pod zemeljskimi pogoji. Navaden težnost Zdi se ogromno, ker so vsi predmeti, ki so nam znani, neverjetno majhni v primerjavi z maso sveta.

Konec 18. stoletja. G merjenje

Prvi poskusi merjenja G so se zgodili konec 18. stoletja. Kot vlečna sila so uporabljali ogromno goro. Ocena pospeška prostega padca je bila narejena na podlagi odstopanja od vertikale teže nihala, ki se nahaja v neposredni bližini gore. S pomočjo geoloških podatkov smo ocenili maso gore in njeno povprečno oddaljenost od nihala. Tako smo dobili prvo, dokaj grobo dimenzijo skrivnostne konstante.

Dimenzije Lorda Cavendisha

Lord Cavendish je v svojem laboratoriju izvedel meritve gravitacijskega privlačenja po metodi prostega tehtanja. Za poskuse so uporabili kovinsko kroglo in masivni kos kovine. Cavendish je pritrdil majhne kovinske kroglice na tanko desko in jim prinesel velike vodilne kroglice. Zaradi udarca se je deska zvila, dokler ni bil učinek privlačnosti kompenziran za Hookejeve sile. Poskus je bil tako prefinjen, da bi tudi najmanjši dih vetra lahko izničil rezultate raziskav. Da bi se izognili konvekciji, je Cavendish postavil vso merilno opremo v veliko škatlo, jo dal v zaprto sobo in opazoval eksperiment s teleskopom.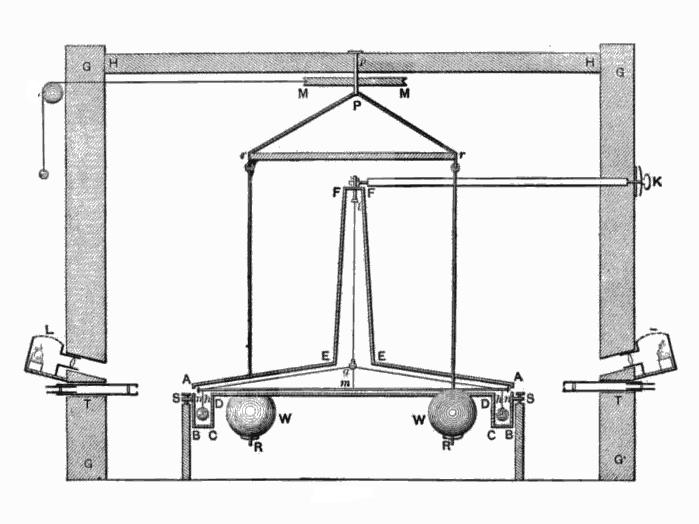

Cavendish je izračunal silo obračanja niti, tako da je vrednost G, ki je bila kasneje le rahlo prilagojena zaradi drugih, natančnejših eksperimentov. V sodobnem sistemu enot:

G = 6,67384 × 10 ^-11 m ³ kg ^-1 s ^-2 .

Ta vrednost je ena od redkih fizikalnih konstant. Njegova vrednost je nespremenljiva na kateri koli točki vesolja.

Merjenje pospeševanja zemlje

Po tretjem Newtonovem zakonu je sila privlačnosti dveh teles odvisna samo od njihove mase in razdalje med njimi. Torej, če na desni strani enačbe nadomestimo množitelj, znan iz drugega zakona Newtona, dobimo:

ma = G (mM) / d2.

V našem primeru se lahko masa m zmanjša in količina a je pospešek, s katerim telo m privablja Zemlja. Trenutno je pospešek gravitacije običajno označen s črko g. Dobimo:

g = GM / d ² .

V našem primeru je d polmer Zemlje, M je njegova masa, G pa je najbolj izmuzljiva konstanta, ki jo fiziki iščejo že vrsto let. Če nadomestimo znane podatke v enačbo, dobimo: g = 9,8 m / s ² . Ta vrednost je pospešek prostega padca na Zemlji.

Vrednosti G za različne zemljepisne širine

Ker naš planet nima oblike krogle, temveč je geoid, njegov polmer ni vedno enak. Zemlja je sploščena, tako da bo pospešek prostega padca prevzel različne vrednosti na ekvatorju in na obeh polih. Na splošno je razlika v odčitkih dolžine radija približno 43 km. Zato se pri fiziki za reševanje problemov vzame pospešek zaradi gravitacije, ki se meri na zemljepisni širini približno 45 ⁰ . Pogosto se za lažje izračune predpostavlja, da je 10 m / s2.

Vrednost G za luno

Naš satelit spoštuje iste zakone kot ostali planeti v sončnem sistemu. Strogo gledano, pri izračunu pospeška na površini lune je treba upoštevati tudi privlačnost s strani sonca. Toda, kot je razvidno iz formule, se z naraščanjem razdalje vrednost privlačnosti močno zmanjša. Zato zavrnitev vseh sekundarnih sil uporablja enako formulo:

G _L = GM / d ² .

Tu je M masa lune in d je njen premer. Če nadomestimo znane vrednosti, dobimo vrednost G _L = 1,622 m / s ² . Ta vrednost je pospešek prostega padca na luni.

To je tako majhna vrednost G _{L, ki} je glavni razlog za odsotnost atmosfere na Luni. Po nekaterih podatkih je v zori časa naš satelit imel atmosfero, vendar ga je zaradi slabe privlačnosti Luna hitro izgubila. Vsi planeti z veliko maso imajo običajno svojo atmosfero. Pospešek prostega padca je dovolj velik, da ne samo, da ne izgubijo lastne atmosfere, temveč tudi da iz prostora vzamejo določeno količino molekularnega plina.

Povzemimo nekaj rezultatov. Pospešek zaradi gravitacije je količina, ki jo ima vsako materialno telo. Ne glede na to, kako presenetljivo se sliši, pa vse, kar ima maso, privlači okoliške predmete k sebi. Samo ta atrakcija je tako majhna, da v vsakdanjem življenju ni pomembna. Kljub temu pa znanstveniki resno razmišljajo tudi o najmanjših fizičnih konstantah, saj vpliv, ki ga imajo na svet okoli nas, ni povsem razumljen.