Kaj je sinus in kosinus v trigonometriji?

Učitelji verjamejo, da bi moral biti vsak učenec sposoben opravljati izračune, poznati trigonometrične formule, vendar ne vsak učitelj razloži, kaj so sinus in kosinus. Kakšen je njihov pomen, kje se uporabljajo? Zakaj govorimo o trikotnikih, v učbeniku pa krog? Poskusimo povezati vsa dejstva skupaj.

Šolski predmet

Študija trigonometrije se običajno začne v razredu 7-8. V tem času se učencem pove, kaj so sinus in kosinus, predlagajo reševanje geometrijskih problemov z uporabo teh funkcij. Kasneje se pojavijo kompleksnejše formule in izrazi, ki jih je treba preoblikovati na algebrski način (formule dvojnih in polkotnikov, močnostne funkcije), delo pa poteka s trigonometričnim krogom.

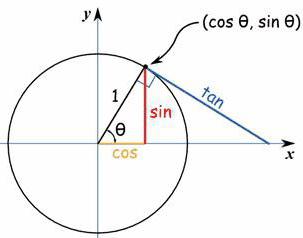Vendar pa učitelji ne morejo vedno jasno razložiti pomena uporabljenih konceptov in uporabnosti formul. Zato učenec pogosto ne vidi smisla v tej temi in zapomnjene informacije se hitro pozabijo. Vendar pa je vredno enkrat razložiti srednješolki, na primer, povezava med funkcijo in nihanjem, logična povezava se bo zapomnila že več let in šale o neuporabnosti teme bodo stvar preteklosti.

Uporaba

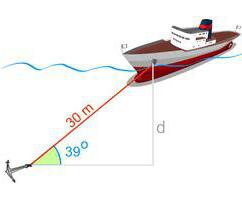
Poglejmo zaradi radovednosti v različnih delih fizike. Želite določiti obseg projektila? Ali izračunati trenje med predmetom in določeno površino? Zibanje nihala, opazovanje žarkov skozi steklo izračuna indukcijo? Praktično v kateri koli formuli se pojavijo trigonometrični koncepti. Torej, kaj je sinus in kosinus?

Definicije

Sinus kota je razmerje med nasprotno nogo in hipotenuzo, kosinus sosednje noge pa je ista hipotenuza. Nič ni zapletenega. Morda so učenci običajno zmedeni zaradi vrednosti, ki jih vidijo v trigonometrični tabeli, ker se pojavijo kvadratne korenine. Ja, poberi se iz njih decimalk ni zelo priročno, ampak kdo je rekel, da morajo biti vse številke v matematiki celo?

Pravzaprav lahko v problematičnih knjigah trigonometrije najdete zabaven namig: večina odgovorov je v tem primeru celo v najslabšem primeru vsebuje dva ali tri korenine. Zaključek je preprost: če dobite v odgovoru »več zgodb«, preverite odločitev o napakah v izračunih ali v argumentih. Najverjetneje jih boste našli.

Kaj morate zapomniti

Kot v vsaki znanosti, v trigonometriji obstajajo taki podatki, ki jih je treba naučiti.

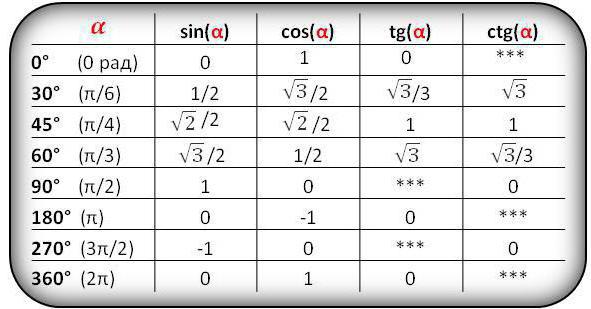
Najprej se spomnite številčnih vrednosti za sinus, kosinus pravokotni trikotnik 0 in 90, kot tudi 30, 45 in 60 stopinj. Te kazalnike najdemo v devetih od desetih šolskih nalog. Prevzamete te vrednote v učbeniku, boste izgubili veliko časa in testa ali izpita ne boste mogli gledati.

Ne smemo pozabiti, da vrednost obeh funkcij ne sme presegati ene. Če nekje v izračunih dobite vrednost izven območja 0-1, se ustavite in ponovno odpravite težavo.

Vsota kvadratov sinusa in kosinusa je enaka eni. Če ste že našli eno od vrednosti, s to formulo poiščite preostalo vrednost.

Teoreme

V osnovni trigonometriji obstajata dva glavna izreka: sinusi in kosinusi.

Prvi pravi, da je razmerje med vsako stranjo trikotnika in sinusom nasprotnega kota enako. Drugi je, da lahko kvadrat katere koli strani dobimo z dodajanjem kvadratov dveh preostalih strani in odštevanjem njihovega dvojnega produkta pomnoženega s kosinusom kota med njimi.

Torej, če je v izrek o kosinusu Nadomestimo vrednost kota 90 stopinj, dobimo ... Pitagorov izrek. Zdaj, če želite izračunati površino številke, ki ni pravi trikotnik, ne morete več skrbeti - oba obravnavana izreka bosta znatno poenostavila rešitev problema.

Cilji in cilji

Proučevanje trigonometrije bo zelo poenostavljeno, ko boste spoznali eno preprosto dejstvo: vsa dejanja, ki jih izvajate, so namenjena doseganju samo enega cilja. Vse parametre trikotnika lahko najdete, če poznate minimalne informacije o njem - to je lahko vrednost enega kota in dolžine dveh strani ali, na primer, treh strani.

Za določitev sinus, kosinus, tangent katerega koli kota teh podatkov je dovolj, z njihovo pomočjo, lahko preprosto izračunate površino slike. Skoraj vedno je za odgovor potrebna ena od omenjenih vrednosti, ki jih lahko najdemo z uporabo enake formule.

Nedoslednosti pri proučevanju trigonometrije

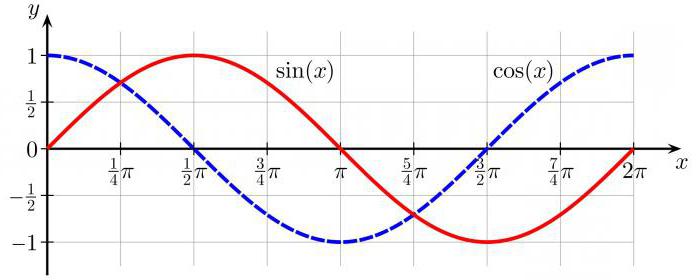
Eno od nejasnih vprašanj, ki se jim študenti raje izogibajo, je iskanje povezave med različnimi koncepti v trigonometriji. Zdi se, da se trikotniki uporabljajo za preučevanje sinusov in kosinusov vogalov, vendar so simboli pogosto prisotni na sliki s krogom. Poleg tega obstaja nerazumljiv valovit graf, imenovan sinusoid, ki nima nobene zunanje podobnosti niti s krogom niti s trikotniki.

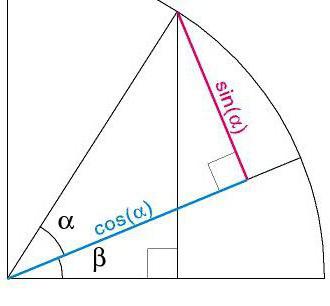Poleg tega se koti merijo v stopinjah, nato v radianih, število Pi, napisano preprosto kot 3,14 (brez enot), se iz nekega razloga prikaže v formulah, ki ustrezajo 180 stopinjam. Kako je vse to povezano?

Merske enote

Zakaj je pi natančno 3,14? Se spomnite, kaj je ta vrednost? To je število polmerov, ki se prilegajo v polkrog. Če je premer kroga 2 centimetra, obseg bo 3,14 * 2 ali 6,28.

Druga točka: morda ste opazili podobnost besed "radian" in "radius". Dejstvo je, da je en radian numerično enak kotu med središčem kroga in lokom z dolžino enega polmera.

Sedaj združimo pridobljeno znanje in razumemo, zakaj je beseda »Pi na pol« zapisana na osi koordinat v trigonometriji, na levi pa »Pi«. To je kotna vrednost, merjena v radianih, ker je polkrog 180 stopinj ali 3,14 radiana. In kjer so stopinje, so sinusi in kosinusi. Trikotnik se enostavno drži od želene točke, tako da segmente postavimo v središče in na os koordinat.

Poglej v prihodnost

Trigonometrija, ki je bila proučena v šoli, se ukvarja s pravokotnim koordinatnim sistemom, kjer je, ne glede na to, kako čudno se sliši, ravna črta ravna črta.

Vendar pa obstajajo tudi bolj zapleteni načini dela s prostorom: vsota kotov trikotnika bo tukaj večja od 180 stopinj, vrstica v našem pogledu pa bo videti kot pravi lok.

Premakni se od besed k dejanjem! Vzemite jabolko. Naredite tri zareze z nožem, tako da boste ob pogledu od zgoraj dobili trikotnik. Odstranite nastali košček jabolka in poglejte "rebra", kjer se skorja konča. Sploh niso neposredni. Sadje v vaših rokah lahko imenujemo krog, zdaj pa si predstavljate, kako kompleksne morajo biti formule, s katerimi lahko najdete območje rezanega kosa. Toda nekateri strokovnjaki vsak dan rešujejo te težave.

Trigonometrične funkcije v življenju

Ste opazili, da ima najkrajša pot letala od točke A do točke B na površini našega planeta izrazito obliko loka? Razlog je preprost: Zemlja je v obliki krogle, kar pomeni, da ne morete veliko izračunati s pomočjo trikotnikov - tukaj morate uporabiti bolj zapletene formule.

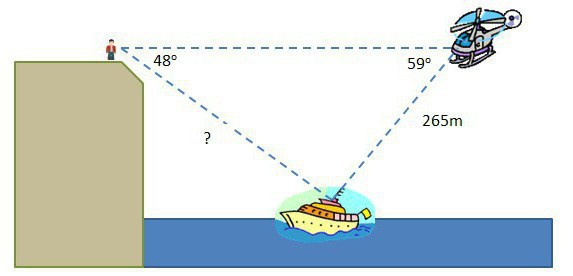
Ne delajte brez sinus / kosinus akutnega kota pri vseh vprašanjih, povezanih s prostorom. Zanimivo je, da se tukaj zbližajo številni dejavniki: trigonometrične funkcije so potrebne pri izračunu gibanja planetov v krogih, elipseh in različnih trajektorijah kompleksnejših oblik; proces izstrelitve raket, satelitov, avtobusov, odklopnih raziskovalnih naprav; opazovanje oddaljenih zvezd in proučevanje galaksij, ki jih človek ne more doseči v bližnji prihodnosti.

Na splošno je področje človekove dejavnosti, ki je lastnik trigonometrije, zelo široko in se bo sčasoma le razširilo.

Zaključek

Danes smo se naučili ali, v vsakem primeru, ponovili, kaj so sinus in kosinus. To so koncepti, ki jih ni treba bati - bi jih želeli in razumeli boste njihov pomen. Ne pozabite, da trigonometrija ni cilj, ampak le orodje, ki ga lahko uporabimo za zadovoljevanje resničnih človeških potreb: gradimo hiše, zagotavljamo prometno varnost, celo raziskujemo odprte prostore vesolja.

Dejansko se zdi sama znanost dolgočasna, toda ko boste v njej našli način, kako doseči svoje cilje, samouresničitev, bo učni proces postal zanimiv in vaša osebna motivacija se bo povečala.

Kot domačo nalogo poskusite najti načine za uporabo trigonometričnih funkcij na področju dejavnosti, ki vas zanima osebno. Predstavljajte si, obrnite se na domišljijo in potem boste zagotovo ugotovili, da vam bo novo znanje koristno v prihodnosti. Poleg tega je matematika koristna za splošni razvoj mišljenja.