Kakšne so metode optimizacije? Metode optimizacije upravljavskih odločitev

Najbolj sprejemljiva rešitev, ki je sprejeta na poslovodni ravni v zvezi s katerim koli vprašanjem, se šteje za optimalno in proces njenega iskanja velja za optimizacijo.

Medsebojna odvisnost in kompleksnost organizacijskih, socialno-ekonomskih, tehničnih in drugih vidikov vodenja proizvodnje je zdaj omejena na odločitve o upravljanju, ki vplivajo na veliko število različnih dejavnikov, ki so med seboj tesno prepleteni, zaradi česar je nemogoče analizirati vsako posamezno z uporabo tradicionalnega analitičnega orodja. metod.

Večina dejavnikov je odločilnega pomena v procesu odločanja in v bistvu ni kvantitativna. Obstajajo tudi tisti, ki so praktično nespremenjeni. V zvezi s tem je bilo potrebno razviti posebne metode, ki lahko zagotovijo izbiro pomembnih upravljavskih odločitev v okviru zapletenih organizacijskih, gospodarskih, tehničnih nalog (strokovne ocene, operativne raziskave in metode optimizacije itd.).

Metode, ki so namenjene raziskovanju operacij, se uporabljajo za iskanje optimalnih rešitev na področjih upravljanja, kot so organizacija proizvodnih in transportnih procesov, obsežno načrtovanje. proizvodnja, material in tehnično oskrbo.

Metode za optimizacijo rešitev so preučevane s primerjavo numeričnih ocen številnih dejavnikov, katerih analiza po tradicionalnih metodah ni možna. Optimalna rešitev je najboljša med možnimi možnostmi gospodarskega sistema in najbolj sprejemljiva glede na posamezne elemente sistema je podoptimalna.

Bistvo operacij raziskovalnih metod

Kot smo že omenili, oblikujejo metode za optimizacijo upravljavskih odločitev. Njihova osnova so matematični (deterministični), verjetnostni modeli, ki predstavljajo proces, aktivnost ali sistem, ki ga proučujemo. Takšen model predstavlja kvantitativno značilnost ustreznega problema. Služijo kot osnova za sprejemanje pomembnih odločitev v procesu iskanja optimalno sprejemljiva možnost.

Seznam vprašanj, ki imajo pomembno vlogo za neposredne vodje proizvodnje in ki se rešujejo med uporabo obravnavanih metod:

• stopnja veljavnosti izbranih rešitev;
• koliko so boljša od alternativnih;
• stopnja upoštevanja odločilnih dejavnikov;
• kakšen je kriterij optimalnosti izbranih rešitev.

Te metode za optimizacijo rešitev (vodstvenih) so namenjene iskanju optimalnih rešitev za čim več podjetij, podjetij ali njihovih oddelkov. Temeljijo na obstoječih dosežkih statističnih, matematičnih in ekonomskih disciplin (teorija iger, čakanje, grafi, optimalno programiranje, matematična statistika).

Metode strokovnega vrednotenja

Te metode optimizacije upravljavskih odločitev se uporabljajo, ko je naloga delno ali v celoti neobdavčena in njene rešitve ni mogoče najti z matematičnimi metodami.

Strokovno znanje je preučevanje zapletenih specifičnih vprašanj v fazi razvoja posebne upravljavske odločitve ustreznih oseb, ki imajo posebno bazo znanja in impresivne izkušnje za pridobitev zaključkov, priporočil, mnenj in ocen. V procesu strokovnega raziskovanja se kot del specialistične specializacije uporabljajo najnovejši dosežki znanosti in tehnologije.

Obravnavane metode optimizacije številnih upravljavskih odločitev (strokovne ocene) so učinkovite pri reševanju naslednjih upravljavskih nalog na področju proizvodnje:

1. Proučevanje kompleksnih procesov, pojavov, situacij, sistemov, za katere so značilne neformalizirane, kvalitativne značilnosti.
2. Razvrščanje in določanje glede na dani kriterij pomembnih dejavnikov, ki so odločilni za delovanje in razvoj proizvodnega sistema.
3. Obravnavane optimizacijske metode so še posebej učinkovite na področju napovedovanja razvojnih trendov proizvodnega sistema in njegove interakcije z zunanjim okoljem.
4. Izboljšanje zanesljivosti strokovnih ocen je v glavnem ciljnih funkcij, ki so kvantitativne in kvalitativne narave, s povprečjem mnenj kvalificiranih strokovnjakov.

In to so le nekatere od metod za optimizacijo številnih upravljavskih odločitev (medsebojni pregled).

Klasifikacija obravnavanih metod

Metode reševanja optimizacijskih problemov, ki temeljijo na številu parametrov, lahko razdelimo na:

• Metode enodimenzionalne optimizacije.
• Optimizacijske metode so večdimenzionalne.

Imenujejo se tudi "numerične optimizacijske metode". Če smo natančni, so to njeni iskalni algoritmi.

V okviru uporabe izvedenih metod so:

• metode neposredne optimizacije (ničelni red);
• gradientne metode (1. vrstni red);
• metode drugega reda itd.

Večina večdimenzionalnih optimizacijskih metod je blizu problema druge skupine metod (enodimenzionalna optimizacija).

Univariate optimizacijske tehnike

Vse numerične optimizacijske metode temeljijo na približnem ali natančnem izračunu njegovih značilnosti, kot so vrednosti ciljne funkcije in funkcij, ki definirajo dopustni niz, njihove izvedenke. Tako je za vsako posamezno nalogo mogoče rešiti vprašanje izbire značilnosti za izračun, odvisno od obstoječih lastnosti zadevne funkcije, razpoložljivih možnosti in omejitev pri shranjevanju in obdelave podatkov.

Obstajajo naslednje metode za reševanje problemov optimizacije (enodimenzionalni):

• Fibonacci metoda;
• dihotomije;
• zlati del;
• dvojni korak.

Metoda Fibonacci

Najprej morate nastaviti koordinate t. X na intervalu [a; b] kot število, ki je enako razmerju razlike (x - a) z razliko (b - a). Zato ima a relativni interval [a; b] koordinata 0 in b - 1, sredina ½.

Če predpostavimo, da sta F0 in F1 medsebojno enaka in vzameta vrednost 1, bo F2 enak 2, F3 - 3, ..., potem Fn = Fn-1 + Fn-2. Fn je Fibonaccijevo število, Fibonaccijevo iskanje pa je optimalna strategija za tako imenovano zaporedno maksimalno iskanje, ker je z njimi precej tesno povezana.

V okviru optimalne strategije je običajno izbrati xn - 1 = Fn - 2: Fn, xn = Fn - 1: Fn. Za enega od obeh intervalov ([0; xn] ali [xn - 1; 1]), od katerih lahko vsak deluje kot zoženi interval negotovosti, bo imela točka (podedovana) glede na novi interval bodisi koordinate [Fn - 3: Fn– 1] ali [Fn-2: Fn-1]. Nadalje, točka je vzeta kot xn - 2, ki ima glede na novo vrzel eno od predstavljenih koordinat. Če uporabimo F (xn - 2), je vrednost funkcije, ki je podedovana iz prejšnje vrzeli, mogoče zmanjšati interval negotovosti in prenesti dedovanje ene vrednosti funkcije.

Na končni stopnji je možno nadaljevati s takšnim intervalom negotovosti, kot je [a; b], medtem ko je srednja točka podedovana od prejšnjega koraka. Kot x1 se nastavi točka, ki ima relativno koordinato ½ + ε, končni interval negotovosti pa [0, ½ + ε] ali [½, 1] glede na [a; b].

V prvem koraku se je dolžina tega intervala zmanjšala na Fn - 1: Fn (iz ene). Pri končnih stopnjah zmanjšanje dolžin ustreznih intervalov predstavljajo številke Fn - 2: Fn - 1, Fn - 3: Fn - 2, ..., F2: F3, F1: F2 (1 + 2ε). Torej bo dolžina takega intervala kot končna različica dobila vrednost (1 + 2ε): Fn.

Če zanemarimo ε, potem je asimptotično 1: Fn enako rn, z n → ∞ in r = (√5 - 1): 2, kar je približno enako 0,6180.

Opozoriti je treba, da asimptotično za pomembno n vsak naslednji korak Fibonačijevega iskanja znatno zoži obravnavani interval z omenjenim koeficientom. Ta rezultat je treba primerjati z 0,5 (koeficient zoženja intervala negotovosti v okviru bisekcijske metode, da bi našli funkcijo nič).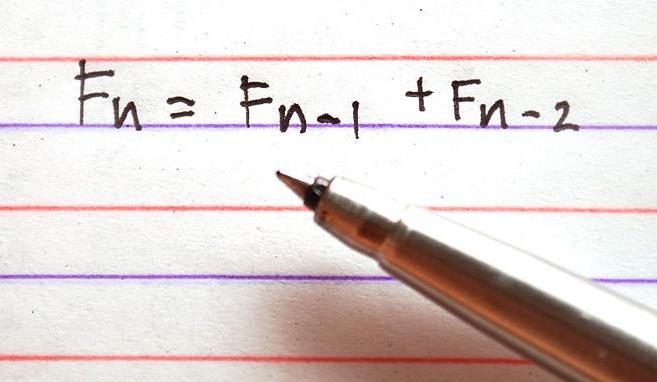

Metoda dihotomije

Če predstavimo določeno objektivno funkcijo, potem moramo najprej poiskati njen ekstrem v intervalu (a; b). Da bi to dosegli, je os abscise razdeljena na štiri enakovredne dele, nato pa je treba določiti vrednost zadevne funkcije na 5 točkah. Nato izberite najmanj. Extremum funkcije mora ležati znotraj intervala (a '; b'), ki je sosednje najnižji točki. Meje iskanja se dvakrat zožijo. In če je najmanjša vrednost v m, A ali b, se ta štirikrat zoži. Novi interval je razdeljen na štiri enake segmente. Ker so bile vrednosti te funkcije na treh točkah določene na prejšnji stopnji, je potrebno izračunati objektivno funkcijo na dveh točkah.

Zlata sekcija

Pri pomembnih vrednostih n so koordinate točk kot xn in xn - 1 blizu 1 - r, enake 0,3820 in r ≈ 0,6180. Gibanje s temi vrednostmi je zelo blizu želeni optimalni strategiji.

Če predpostavimo, da je F (0,3820)> F (0,6180), potem je določen interval [0; 0,6180]. Ker pa je 0.6180 * 0.6180 ≈ 0.3820 ≈ xn-1, je na tej točki F že znano. Posledično je na vsaki stopnji, začenši od drugega, potreben le en izračun objektivne funkcije in vsak korak zmanjša dolžino obravnavanega intervala s faktorjem 0,6180.

Za razliko od Fibonaccijevega iskanja ta metoda ne zahteva določitve števila n, še preden se začne iskanje.

"Zlati del" odseka (a; b) je odsek, kjer je razmerje med njegovo dolžino r in večjim delom (a; c) enako razmerju med večjim delom r in manjšim, to je (a; c) do (c; b). Ni težko uganiti, da je r določen z zgornjo formulo. Torej, s pomembno n, Fibonacci metoda gre v to.

Metoda podvojitve koraka

Bistvo je iskanje smeri zmanjšanja ciljne funkcije, gibanja v tej smeri v primeru uspešnega iskanja s postopno naraščajočim korakom.

Najprej določimo začetno koordinato M0 funkcije F (M), najmanjšo vrednost koraka h0, smer iskanja. Nato definiramo funkcijo v m. Nato naredite korak in na tej točki poiščite vrednost te funkcije.

Če je funkcija manjša od vrednosti, ki je bila na prejšnjem koraku, morate opraviti naslednji korak v isti smeri, ko ste ga prej dvakrat povečali. Ko je njegova vrednost večja od prejšnje, boste morali spremeniti smer iskanja in se s korakom h0 začeti premikati v izbrani smeri. Predstavljeni algoritem se lahko spremeni.

Večdimenzionalne metode optimizacije

Zgornja metoda ničelnega reda ne upošteva izvedenih instrumentov minimizirane funkcije, tako da je njihova uporaba lahko učinkovita v primeru kakršnih koli težav pri izračunu izvedenih finančnih instrumentov.

Skupina metod prvega reda se imenuje tudi gradient, ker se gradient te funkcije uporablja za določitev smeri iskanja - vektorja, katerega komponente so delni izvedeni minimizirani funkciji glede na ustrezne optimizirane parametre.

V skupini metod drugega reda so uporabljeni 2 izvedenki (njihova uporaba je precej omejena zaradi težav pri izračunu).

Seznam metod brezpogojne optimizacije

Če uporabljamo večdimenzionalno iskanje brez uporabe izvedenih finančnih instrumentov, so brezpogojne optimizacijske metode naslednje:

• Hook in Jeeves (izvedba dveh vrst iskanja - na modelu in raziskovanje);
• minimiziranje pravilnega simpleksa (iskanje minimalne točke ustrezne funkcije s primerjavo na vsaki posamezni iteraciji njegovih vrednosti v tockah simpleksa);
• ciklični koordinatni spust (z uporabo koordinatnih vektorjev kot referenčnih točk);
• Rosenbrock (temelji na uporabi enodimenzionalnega minimiziranja);
• zmanjšanje z deformiranim simpleksom (sprememba metode minimizacije z navadnim simpleksom: dodajanje postopka stiskanja, razširitev).

V situaciji uporabe izvedenih finančnih instrumentov v procesu večdimenzionalnega iskanja se razlikuje metoda najhitrejšega spuščanja (najbolj temeljni postopek za minimiziranje diferencialne funkcije z več spremenljivkami).

Razlikujejo tudi metode, ki uporabljajo konjugirane smeri (Davidon-Fletcher-Powellova metoda). Njegovo bistvo je predstavitev smeri iskanja kot Dj * grad (f (y)).

Klasifikacija matematičnih metod optimiranja

Konvencionalno, glede na dimenzijo funkcij (cilj), so:

• z eno spremenljivko;
• večdimenzionalna.

Glede na funkcijo (linearno ali nelinearno) obstaja veliko število matematičnih metod, ki so namenjene iskanju ekstremov za reševanje problema.

Glede na kriterij za uporabo izvedenih finančnih instrumentov so matematične optimizacijske metode razdeljene na:

• metode za izračun 1 derivata ciljne funkcije;
• večdimenzionalna (1. derivat - vektorska količina - gradient).

Na podlagi učinkovitosti izračuna obstajajo:

• hitre metode izračunavanja ekstremov;
• poenostavljeno računanje.

To je pogojna klasifikacija obravnavanih metod.

Optimizacija poslovnih procesov

Metode lahko tukaj uporabimo drugače, odvisno od težav, ki jih je treba rešiti. Običajno je treba za optimizacijo poslovnih procesov izbrati naslednje metode:

• izjeme (zmanjšanje obstoječih procesnih ravni, odpravljanje vzrokov motenj in vhodnega nadzora, zmanjšanje transportnih poti);
• poenostavitve (olajšanje prehoda naročila, zmanjšanje zapletenosti strukture izdelka, porazdelitev dela);
• standardizacija (uporaba posebnih programov, metod, tehnologij itd.);
• pospeševanje (vzporedno načrtovanje, stimulacija, operativno načrtovanje prototipov, avtomatizacija);
• spremembe (spremembe na področju surovin, tehnologij, delovnih metod, lokacije osebja, sistemov dela, količine naročila, postopka obdelave);
• zagotavljanje interoperabilnosti (v smislu organizacijskih enot, osebja, sistema dela);
• izbor in vključevanje (glede potrebnih procesov, komponent).

Davčna optimizacija: metode

Ruska zakonodaja daje davkoplačevalcem zelo bogate možnosti za zmanjšanje zneskov davkov, zato je običajno, da se opredelijo takšne metode, ki jih želijo čim bolj zmanjšati, kot so splošne (klasične) in posebne.

Splošne metode davčne optimizacije so naslednje:

• izdelava računovodske usmeritve družbe z največjo možno uporabo priložnosti, ki jih nudi ruska zakonodaja (postopek odpisa IBE, izbira metode za izračun prihodkov od prodaje blaga itd.);
• optimizacija s pogodbo (sklepanje privilegiranih transakcij, jasna in kompetentna uporaba besedil itd.);
• uporabo različnih vrst dajatev, davčne oprostitve.

Drugo skupino metod lahko uporabljajo tudi vsa podjetja, vendar imajo še vedno dokaj omejen obseg. Posebne metode davčne optimizacije so naslednje:

• zamenjava odnosov (operacija, ki predvideva obremenjujoče obdavčevanje, se nadomesti z drugo, ki omogoča doseganje podobnega cilja, hkrati pa se uporablja preferencialni davčni postopek).
• ločitev odnosov (zamenjava le dela poslovne transakcije);
• odlog plačila davka (odlog trenutka nastanka davčna postavka za drugo koledarsko obdobje);
• neposredno zmanjšanje obdavčljivega predmeta (reševanje številnih obdavčljivih transakcij ali premoženja brez negativnega vpliva na glavno gospodarsko dejavnost družbe).