Trigonometrija iz nič: osnovni pojmi, zgodovina

Sinus, kosinus, tangenta - ko izgovarjate te besede v prisotnosti srednješolcev, ste lahko prepričani, da jih bo dve tretjini izgubilo zanimanje za nadaljnji pogovor. Razlog je v tem, da se osnove trigonometrije v šoli poučujejo v popolni izolaciji od resničnosti, zato učenci ne vidijo smisla v študiju formul in izrekov.

Pravzaprav se po podrobnejšem pregledu to področje znanja izkaže za zelo zanimivo in uporabno - trigonometrija se uporablja v astronomiji, gradbeništvu, fiziki, glasbi in na mnogih drugih področjih.

Spoznajmo se z osnovnimi pojmi in navedli bomo več razlogov za študij tega oddelka matematične znanosti.

Zgodovina

Ni znano, kdaj je človeštvo začelo ustvarjati prihodnjo trigonometrijo iz nič. Dokumentirano je bilo, da so Egipčani že v drugem tisočletju pred našim štetjem poznali osnove te znanosti: arheologi so našli papirus z nalogo, v kateri je treba najti kot nagiba piramide na dveh znanih straneh.

Večji uspeh so dosegli znanstveniki iz starodavnega Babilona. Skozi stoletja so v astronomiji obvladovali številne izreke, uvedli posebne načine za merjenje kotov, ki jih danes, mimogrede, uporabljamo: stopnje, minute in sekunde si je evropska znanost izposodila v grško-rimski kulturi, v kateri so te enote prišli iz Babiloncev.

Domneva se, da je bil slavni pitagorejski izrek, povezan z osnovami trigonometrije, babiloncem znan pred skoraj štirimi tisoč leti.

Ime

Dobesedno lahko izraz "trigonometrija" prevedemo kot "merilni trikotniki". Glavni predmet študija v tem delu znanosti je bil več stoletij pravokotni trikotnik oziroma razmerje med velikostjo kotov in dolžinami njegovih strani (danes se študija trigonometrije od začetka začne s tem odsekom). V življenju so pogoste situacije, ko je nemogoče praktično izmeriti vse zahtevane parametre predmeta (ali razdalje do objekta), potem pa je potrebno z izračunom pridobiti manjkajoče podatke.

V preteklosti na primer oseba ni mogla izmeriti razdalje do prostorski objekti toda poskusi izračuna teh razdalj se pojavijo veliko pred prihodom naše dobe. Trigonometrija je prav tako igrala pomembno vlogo pri plovbi: kapetan je vedno imel znanje, ki ga je lahko vedno navigiral z zvezdami in prilagodil smer.

Osnovni pojmi

Da bi obvladali trigonometrijo od začetka, morate razumeti in zapomniti nekaj osnovnih izrazov.

Sinus določenega kota je razmerje nasprotne noge do hipotenuze. Pojasnjujemo, da je nasprotna noga stran, nasprotna kotu, ki ga obravnavamo. Torej, če je kot 30 stopinj, bo sinus tega kota za vsako velikost trikotnika vedno ½. Kosinus kota je razmerje med sosednjim krakom in hipotenuzo.

Tangenta je razmerje nasprotne noge do sosednjega (ali, enakovredno, razmerje med sinusom in kosinusom). Kotangens je enota, deljena s tangento.

Pomembno je omeniti slavno Pi (3.14 ...), ki predstavlja polovico obseg s polmerom ene enote.

Priljubljeni hrošči

Ljudje, ki študirajo trigonometrijo od začetka, naredijo vrsto napak - večinoma iz nepazljivosti.

Najprej je treba pri reševanju problemov v geometriji upoštevati, da je uporaba sinusov in kosinusov možna le v pravokotnem trikotniku. Zgodi se, da študent »na stroju« vzame najdaljšo stran trikotnika za hipotenuzo in dobi napačne rezultate izračunov.

Drugič, najprej je mogoče z lahkoto zamenjati vrednosti sinusnega in kosinusnega za izbrani kot: spomnimo se, da je sinus 30 stopinj numerično enak kosinusu 60 in obratno. Pri zamenjavi napačne številke bodo nadaljnji izračuni napačni.

Tretjič, dokler problem ni popolnoma rešen, ne zaokrožite nobenih vrednosti, izvlecite korenine, zapišite navaden del kot decimalno. Učenci si pogosto prizadevajo pridobiti »lepo« število v nalogi trigonometrije in takoj izvlečejo koren iz treh, čeprav se lahko v enem samem dejanju ta koren zmanjša.

Etimologija besede "sinus"

Zgodovina besede "sinus" je resnično nenavadna. Dejstvo je, da dobesedni prevod te besede iz latinščine pomeni "votlo". To je zato, ker je bilo pri prevajanju iz enega jezika v drugega izgubljeno pravilno razumevanje besede.

Imena osnovnih trigonometričnih funkcij izvirajo iz Indije, kjer je pojem sinusov označen z besedo "bowstring" v sanskrtu - dejstvo je, da je segment skupaj z lokom kroga, na katerem je temeljil, podoben loku. V času razcveta arabske civilizacije so bili izposojeni indijski dosežki na področju trigonometrije, izraz pa je bil prenesen v arabski jezik v obliki prepisa. Tako se je zgodilo, da je v tem jeziku že obstajala podobna beseda, ki označuje votlino, in če so Arabci razumeli slišno razliko med domačo in izposojeno besedo, potem so Evropejci, ki so prevedli znanstvene trakove v latinščino, dobesedno prevedli arabsko besedo, brez povezave s pojmom sinus . Uporabljamo jih do danes.

Tabele vrednosti

Obstajajo tabele, v katere se vnesejo številske vrednosti za sinus, kosinus in tangente vseh možnih kotov. V nadaljevanju so predstavljeni podatki za kote 0, 30, 45, 60 in 90 stopinj, ki jih je treba naučiti kot obvezni del trigonometrije za lutke, koristnost njihovega spomina pa je precej enostavna.

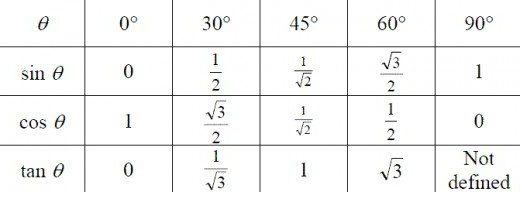Če se zgodi, da je numerična vrednost sinusnega ali kosinusnega kota "odletela iz glave", obstaja način, da jo sami izpeljete.

Geometrična predstavitev

Narišite krog, skozi njegovo središče pa narišemo absciso in ordinate. Osi abscise se nahaja vodoravno, osi ordinate je navpično. Ponavadi so podpisane kot »X« in »Y«. Zdaj iz središča kroga narišemo črto tako, da dobimo kot med njo in osjo X. Končno, od točke, kjer se premica križa s krogom, spustimo pravokotno na os X. Dolžina dobljenega segmenta bo enaka številčni vrednosti sinusa našega kota.

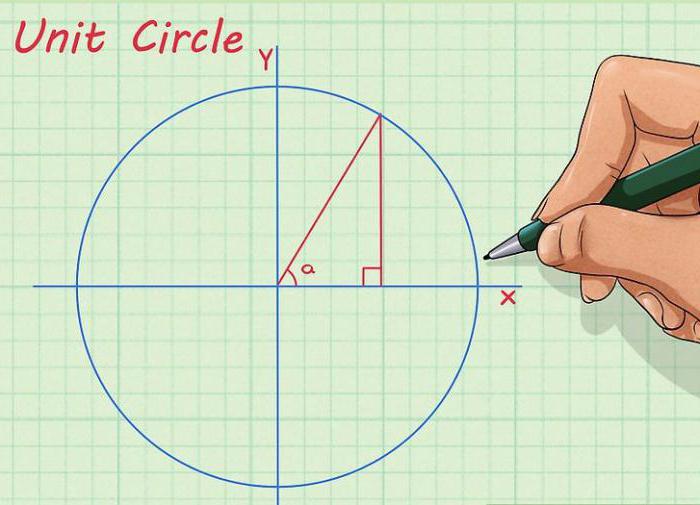Ta metoda je zelo pomembna, če ste pozabili na želeno vrednost, na primer na izpitu, in ni priročnika o trigonometriji. Točne številke ne boste dobili na ta način, vendar boste zagotovo videli razliko med ½ in 1,73 / 2 (sinus in kosinus pod kotom 30 stopinj).

Uporaba

Eden prvih strokovnjakov, ki so uporabljali trigonometrijo, so bili mornarji, ki niso imeli nobene druge referenčne točke na odprtem morju, razen neba nad njihovimi glavami. Danes so kapitani ladij (letala in drugo) vrste prevoza) Ne iščejo najkrajše poti skozi zvezde, temveč aktivno uporabljajo GPS navigacijo, kar bi bilo nemogoče brez uporabe trigonometrije.

V skoraj vsakem fizikalni odsek Čakate na izračune s sinusi in kosinusi: ali je uporaba sile v mehaniki, izračuni poti predmetov v kinematiki, nihanje, širjenje valov, lom svetlobe - ne morete brez osnovne trigonometrije v formulah.

Še en poklic, ki je nepredstavljiv brez trigonometrije, je geodet. Z uporabo teodolita in ravni ali bolj kompleksne naprave - tahiometra, ti ljudje merijo razliko v višini med različnimi točkami na zemeljski površini.

Ponovljivost

Trigonometrija se ne ukvarja le z koti in stranicami trikotnika, čeprav je od te točke začela obstajati. Na vseh področjih, kjer je cikličnost (biologija, medicina, fizika, glasba itd.), Boste naleteli na urnik, katerega ime verjetno veste sinusni val.

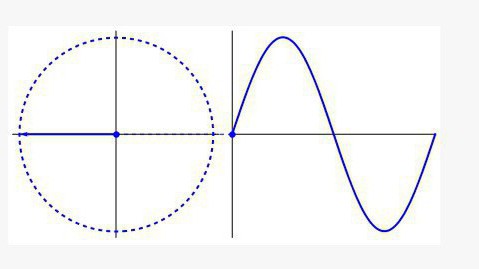Tak graf je krog, ki se razvija vzdolž časovne osi in izgleda kot val. Če ste kdaj v razredu fizike delali z osciloskopom, razumete, o čem gre. Tako glasbeni izenačevalnik kot naprava, ki prikazuje srčne ritme, uporabljata trigonometrične formule v svojem delu.

Za zaključek

Če razmišljamo o tem, kako se naučiti trigonometrije, jih večina dijakov in srednješolcev šteje za zapleteno in nepraktično znanost, saj se z učbenikom seznanijo le z dolgočasnimi informacijami.

V zvezi z nepraktičnostjo - smo že videli, da je v različnih stopnjah potrebna sposobnost rokovanja s sinusi in tangenti na skoraj vseh področjih dejavnosti. Kar se tiče kompleksnosti ... Pomislite: če so ljudje to znanje uporabljali pred več kot dva tisoč leti, ko je imel odrasli manj znanja kot današnji srednješolci, ali je res mogoče, da to področje znanosti preučite na osnovni ravni? Nekaj ​​ur premišljenega pouka z reševanjem problemov - vaš cilj boste dosegli s preučevanjem osnovnega tečaja, tako imenovane trigonometrije za lutke.