Drevo odločanja je primer. Metode odločanja

V večini primerov se odločanje lahko izvede s svetlobno hitrostjo, ki temelji na naših izkušnjah, kot pravijo, z očmi. Včasih pa ta možnost ni primerna. In kaj storiti v tem primeru? Še posebej za te pametne ljudi so razvili metode odločanja. Omogočajo postopno in z minimalnimi odstopanji izdelavo algoritma ukrepov.

Splošne informacije

In najbolj zanimiv trenutek za nas je metoda drevesa odločanja. Kakšen je? Kje se uporablja? Metoda drevesa odločitev je grafični prikaz določenih dejanj in stanj okolja, ki kažejo ustrezne verjetnosti in dobitke za določene kombinacije. Uporablja se za ocenjevanje tveganj pri projektih, ko je potrebno vložiti sredstva za daljše časovno obdobje. Razlog za njegovo uporabo je, da imate dva ali več zaporednih sklopov rešitev. Te bi morale teči iz prejšnjega in / ali niza stanja okolja.

O formalni strukturi

Kateri elementi se uporabljajo za ustvarjanje? To je:

1. Rešitveno vozlišče. Uporablja se za označevanje trenutka izbire.
2. Črta, ki predstavlja alternativo.
3. Vozlišče dogodka Uporablja se za označevanje določene naključnosti.
4. Vrstica, ki opisuje okolje, ki je posledica nepredvidenega dogodka.
5. Rezultat vozlišče. Uporablja se za prikaz skupnih vrednosti. Povezano je s specifičnim stanjem okolja in odločitvami.
6. Node, ki označuje vmesni rezultat. Treba je navesti situacijo, ko je treba sprejeti drugo odločitev.

Gradnja

Kako se v praksi uporablja metoda odločitvenega drevesa? Za oblikovanje različnih razvojnih scenarijev je potrebno imeti vse potrebne in zanesljive informacije, ki upoštevajo verjetnosti in čas nastanka določenih dogodkov in rezultatov. Na začetku se zbirajo podatki. To storite tako, da uporabite naslednji algoritem:

1. Določena je sestava in trajanje faz življenjskega cikla;
2. Predvideni so ključni dogodki, ki bodo vplivali (ali se lahko spremenili) na nadaljnji razvoj;
3. Določi se čas njihovega nastanka;
4. Oblikovane so vse možne rešitve, ki se obravnavajo kot možnosti za ključne dogodke;
5. Določena je verjetnost njihovega sprejetja;
6. Ocenjeni stroški faz v tekočih cenah.

Na pridobljenih podatkih je povsem mogoče izdelati drevo odločitev. Vsebuje vozlišča, ki se štejejo za ključne dogodke. V bistvu so to odločitvene točke. Pridružijo se jim veje - to so nekatera dela, katerih cilj je doseči določen rezultat. Z izgradnjo drevesa odločitev lahko izračunate verjetnost za vsak izbrani scenarij. Poleg tega je pozornost namenjena tudi drugim bistveno pomembnim kazalnikom, ki so potrebni za analizo tveganja in sprejetje učinkovitih ukrepov upravljanja. Treba je opozoriti, da se ta metoda običajno uporablja za projekte, ki imajo več možnih možnosti. V nasprotnem primeru postane shema preveč obsežna, zaradi česar je težko izračunati optimalno rešitev in izbrati potrebne podatke. Razumevanje, kako narediti drevo odločanja, bi se moralo že oblikovati. Oglejmo si primere.

Naložbeni projekti

Najboljši način za pojasnitev drevesa odločanja je primer iz življenja. Zato je bolje začeti z njo in ne z abstraktno matematiko. Recimo, da imamo na voljo tri naložbene projekte. Označujemo jih kot IP1, IP2 in IP3. Denimo, da za njihovo izvajanje je treba vlagati oziroma 200, 300 in 500 milijonov rubljev. Pričakovani dobiček je 100, 200 in 300 milijonov rubljev. Obstaja tveganje izgube denarja. Verjetnost takšnega scenarija je 10%, 5% in 20% za vsako od možnosti. Kaj je bolje izbrati? Iskanje povsem matematičnega odgovora je zelo težko. Toda z uporabo drevesa odločanja je ta naloga veliko lažja. Na začetku je potrebno izdelati drevo odločitev o naložbenem projektu. Ko je zgrajen, ga začnemo raziskovati z uporabo povratne analize. Pojdite na sliko od desne proti levi. Če vstopimo v kroge, moramo v njih postaviti matematične vrednosti pričakovanja plačil. V našem primeru bo rezultat videti takole:

1. 100 * 0,9 - 200 * 0,1 = 70;
2. 200 * 0,95 - 300 * 0,05 = 175;
3. 300 * 0,8 - 500 * 0,2 = 140.

Na podlagi izračunov je enostavno videti, da je IP2 najbolj koristen za nas. Zdaj pa se potopimo v matematiko in razmislimo o nekaterih abstraktnih problemih na drevesu odločanja.

Najpreprostejši primer

V tem primeru bomo imeli samo dve možnosti - »ne« ali »da«. Ali pa bomo v jeziku logične logike imeli 0 ali 1. Razumevanje takega primera drevesa odločanja je lahko težavno, zato bomo uporabili »ne« ali »da«. Recimo, da smo na voljo za delo za 160 rubljev na uro. Lahko rečemo ne, in potem se nič ne bo spremenilo. Ali pa rečemo »da« in potem, ko smo malo delali, lahko občutimo, kako je v žepu postal težji za 160 rubljev. Model lahko nekoliko zapletete, v primeru dogovora pa dodate še nadaljevanje. Na primer - trdo delajte? Če "da", potem plačilo 300 rubljev, če "ne", potem ostane na isti ravni 160.

Izdelava strategij življenjskega vedenja

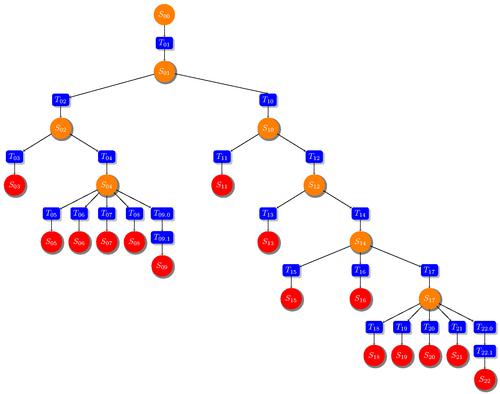
Mnogim se zdi, da se primer drevesa odločanja uporablja samo za velike naložbe in abstraktne matematične raziskave. Ampak ni. Seveda lahko zapomniš teorijo. Lahko ga sprejmete in zmagate. In zdaj bomo pogledali formulo, ki jo je predlagal Jean-Paul Getty, imenovan »Kako postati bogat«. Na kratko se izrazi: "Vstani zgodaj," "Trdo delaj," "Najdi olje." Oglejmo si modeliranje zaporedja odločitev:

1. Izbrati moramo med »Vstani zgodaj« in »Spi prepozno«. To je najpreprostejša izbira.
2. Izbrati moramo med "trdo delati" in "po rokavih". To je tudi najpreprostejša izbira.
3. Hkrati se lahko dogodek »Najdeno olje« pojavi z določeno verjetnostjo. Njegova vrednost je odvisna od zaporedja naših odločitev.

Če najdemo olje, potem smo postali bogati. Ni najdenih vlog - to pomeni, da obstajajo samo izgube, poraba za iskanje. In če boste prepozno spali in delali brezskrbno, potem ne morete niti iskati olja. Najprimernejša možnost je »Vstani zgodaj« in »Trdo delaj«.

Iščemo naše olje

In zdaj za izračune. Obravnavani primer drevesa odločanja je bolje pojasnjen z uporabo tabel. Recimo, da delamo optimalno. Potem naša možnost:

Kot lahko vidite, najbolj donosna možnost ponuja zelo dobre možnosti. Ali je možno v celoti uporabiti to tabelo za prikaz tega primera? Da, in ni tako težko, kot se zdi na prvi pogled:

Ta primer drevesa odločitev nam jasno kaže, da je ključ do uspeha trdo delo. Velikost delovnega dne nas lahko približa cilju, da postanemo bogati in povečamo velikost države. Čeprav so seveda tu podatki precej posplošeni, upamo pa, da je splośni miselni razum razumljiv.

Boljši primer

Nekdo bi lahko trdil - no, drevo odločanja je koristno. Vendar so obravnavane možnosti preveč pretirane in uporaba v realnem položaju je precej problematična. To mnenje ima pravico do obstoja, vendar samo za tiste, ki niso razumeli. Odločitveno drevo je lahko precej zapleteno in bolj prilagodljivo. Zato bomo nekoliko izboljšali primer olja. In tokrat moramo upoštevati vračilo. Recimo, da se sredstva za iskanje nafte porabijo takoj. Če najdemo mineral, potem se bodo vse naložbe, ki so bile izvedene v raziskovanju, takoj izplačale. Prihodki bodo prispeli v dveh letih. Kot lahko vidite, imamo prejemke in plačila razpršena v celotnem časovnem obdobju. In priskrbeti moramo vse zneske za razpoložljivi denar. Recimo, da je diskontna stopnja 20%, potem bo naša formula za osebo, ki trdo dela in zgodaj vstala, videti takole: (0,1 * 10 000 000) / 1,22 + 0,9 (-200 000) = 514 444. Pri drugih variantah dejavnosti bodo vrednosti: 157.222, - 128.555 in - 200.000 rubljev. Strinjam se, da je to bolj kot utemeljitev za projekt! Kljub dejstvu, da so se ravni dohodkov zmanjšale, je še vedno najučinkovitejša možnost za trdo delo in zgodnje vstajanje. Potem, kako spati pozno ne pritegne. In kaj odločanje je koristno za nas, tako v življenju kot v izračunih?

Zgrejte primer

Bralcem ponujamo utrditev znanja. Recimo, da imamo dok. Proizvaja izdelke P1 v višini 1 tisoč enot. Vodja DOK meni, da se trg blaga P2 širi. Izvedene so bile študije, ki so omogočile določitev predlaganih razvojnih možnosti: P1mak = 1000; P1min = 5000; P2mak = 8000; P2min = 4000. Tukaj min in mak je verjetnost povpraševanja po določeni količini blaga. To pomeni, da tisoč P1 ni problem za izvedbo. Ampak 5000 morda ne bo mogel. Verjetnost povpraševanja je: C1mak = 0,7; C1min = 1-C1mak = 0,3; S2mak = 0,6; C2min = 1 - C2mak = 0,4. Na enoto blaga P1 ustvarimo dobiček v višini 1 denarne enote. Za A2 je ta številka 0,9. Vendar pa obstaja težava - minimalno povpraševanje po obeh proizvodih presega obstoječe in razpoložljive zmogljivosti MLC. Kakšni bodo stroški (zdaj enaki K) za podvojitev za vzporedno proizvodnjo v ekvivalentu, če:

1. stroški so K = 0,4 * 103 denarnih enot;
2. ekvivalentna količina P1 = 1000 in P2 = 900;
3. največje in tekoče povpraševanje za P1 in P2 je: (K1mak = 2 * 103; K1min = 1,4 * 103) in (K2mak = 1,2 * 103; K2min = 0,8 * 103).

In ob takih podatkih je treba ugotoviti, ali je priporočljivo nadomestiti proizvedene izdelke in razviti zmogljivosti.

Reševanje problemov

Ali je težko sami ugotoviti? No, majhen namig - lahko uporabite algoritem, ki je bil uporabljen v primeru z oljem. Za tiste, ki tega niso mogli, bo napisana rešitev. Na začetku ugotavljamo posledice naših odločitev za proizvodnjo ene vrste (P1 ali P2). Nato raziščite možnost z obema. V ta namen zavržemo iracionalne ukrepe za razvoj zmogljivosti in ločeno označimo podatke o možnih dobičkih v stolpcu. Upoštevamo verjetnost povpraševanja in ocenimo povprečno učinkovitost na posameznih točkah. Če izracunamo, bomo videli, da je pri dolgotrajni proizvodnji izdelkov P1 za nas bolj koristno pri razvoju zmogljivosti in hkratni proizvodnji kot pa prehod na en P2. Čeprav je to, če minimalna pričakovanja. Kaj pa največje povpraševanje? V tem primeru moramo narisati drugo vejo, ki bo obravnavala to rešitev. Da bi izračunali njegovo učinkovitost, povzemamo prvo in drugo možnost ter odštejemo stroške podvajanja zmogljivosti. In izkaže se, da je to najbolj donosna rešitev. Zato smo prišli do zaključka, da je potrebno razviti zmogljivosti in zagotoviti hkratno sproščanje P1 in P2.

Postavite cilje

To je drevo odločanja. Primeri reševanja tveganj nam omogočajo, da razumemo to metodo in jo sprejmemo. Seveda lahko na začetku pride do določenih težav, vendar se s prakso uspešno rešujejo. Pri tem lahko pomagajo knjige iz matematike, ekonometrije, kibernetike in številnih drugih disciplin.

Sposobnost avtomatizacije

Metode odločanja imajo jasno strukturo. Zato lahko računalniške tehnologije z njimi delajo precej enostavno. Kot drug primer, postopek izdaje posojila v banki. Hkrati je za računalnik prikazano drevo odločanja v obliki logičnega konstrukta »če ... potem ...«. Čeprav, mimogrede, temelji tudi na tem načelu tudi za ljudi, vendar je treba pri interakciji s tehnologijo osredotočiti pozornost na to. Recimo, da je prvi korak vprašanje starosti. Če je oseba stara manj kot štirideset let, potem se sprašujejo o njegovem izobraževanju in plačah. Več - obstaja hiša. Odgovor je da - izdajamo posojilo. Negativno - vprašajte o višini dohodka. Manj kot 20 tisoč rubljev na mesec - zavrnemo. To je hitro in učinkovito.

Zaključek

Če obstaja več načinov vedenja in scenarijev, potem uporabite drevo odločitev, da najdete najboljše stanje. Omogočila bo dajanje vseh razpoložljivih informacij in izračunov na papir in izboljšanje učinkovitosti odločanja.