Posebna teorija relativnosti. Einsteinova posebna in splošna relativnost

Po tem, ko so matematiki ustvarili pravila v prostoru pojmov in števil, so znanstveniki prepričani, da morajo le poskusiti in razložiti strukturo vseh stvari s pomočjo logičnih konstrukcij. V razumnih mejah delujejo zakoni matematike. Toda eksperimenti, ki presegajo dnevne koncepte in koncepte, zahtevajo nova načela in zakone.

Ideja

Sredi 19. stoletja se je povsod razširila ustaljena ideja o univerzalni oddaji, ki jo je razširil večina znanstvenikov in raziskovalcev. Skrivnostni eter je postal najpogostejši model, ki razlaga fizikalne procese, ki so bili takrat znani. Toda za matematični opis hipoteze etra so postopoma dodali številna nerazložljiva dejstva, ki so bila pojasnjena z različnimi dodatnimi pogoji in predpostavkami. Postopoma so harmonična teorija etra, ki je prerasla v "bergle", postala preveč. Za razlago strukture našega sveta so bile potrebne nove ideje. Postulati posebne teorije relativnosti so izpolnjevali vse zahteve - bili so kratki, dosledni in v celoti potrjeni z eksperimenti.

Michelsonov poskus

Zadnja slama, ki je prekinila hipotezo etra, je bila raziskava na področju elektrodinamike in Maxwellove enačbe, ki ju je razložila. Pri uvajanju rezultatov poskusov v matematično rešitev je Maxwell uporabil teorijo etra.

V svojem poskusu so raziskovalci prisilili dva žarka, ki gredo v različnih smereh, da sinhrono sevata. Pod pogojem, da se svetloba premika v "etru", bi se moral en žarek svetlobe premakniti počasneje od drugega. Kljub številnim ponovitvam izkušenj je bil rezultat enak - se je svetloba premikala s konstantno hitrostjo.

V nasprotnem primeru ni bilo mogoče pojasniti dejstva, da je bila po izračunih hitrost svetlobe v hipotetičnem etru vedno ista, ne glede na hitrost, s katero se je opazovalec gibal. Da bi pojasnili rezultate raziskave, je bilo potrebno, da je referenčni okvir »idealen«. To je nasprotovalo Galileovemu postulatu o invarialnosti vseh inercialnih referenčnih sistemov.

Nova teorija

V začetku dvajsetega stoletja je cela galaksija znanstvenikov začela razvijati teorijo, ki bi uskladila rezultate študij elektromagnetnih nihanj z načeli klasične mehanike.

Pri razvoju nove teorije je bilo upoštevano, da:

- gibanje s hitrostmi v bližini svetlobe spremeni formulo Newtonovega drugega zakona, ki povezuje pospešek s silo in maso;

- enačba za impulz telesa imeti drugačno, bolj zapleteno formulo;

- hitrost svetlobe ne glede na izbrani referenčni sistem.

Prizadevanja A. Poincaréa, G. Lorenza in A. Einsteina so privedla do oblikovanja posebne teorije relativnosti, ki se je strinjala z vsemi pomanjkljivostmi in pojasnila obstoječa opažanja.

Osnovni pojmi

Osnova posebne teorije relativnosti je v definicijah, s katerimi deluje ta teorija.

1. Referenčni sistem je materialno telo, ki se lahko vzame kot začetek referenčnega sistema in časovna koordinata, v kateri opazovalec spremlja gibanje predmetov.

2. Inercialni referenčni sistem je tisti, ki se premika enakomerno in neposredno.

3. Dogodek. Posebna in splošna teorija relativnosti dogodek obravnavamo kot prostorsko lokaliziran fizični proces z omejenim trajanjem. Koordinate objekta lahko določite v tridimenzionalni prostor kot (x, y, z) in časovno obdobje t. Standardni primer takšnega procesa je svetloba.

Posebna teorija relativnosti obravnava inercialne referenčne sisteme, v katerih se prvi sistem premika v bližini druge s konstantno hitrostjo. V tem primeru je iskanje relacij objektnih koordinat v teh inercialnih sistemih prednostna naloga SRT in je vključena v njene glavne naloge. Posebna teorija relativnosti je to vprašanje rešila s pomočjo Lorentzovih formul.

STO postulati

Pri razvoju teorije je Einstein zavrnil vse številne predpostavke, ki so bile potrebne za podporo teoriji etra. Preprostost in matematična dokazljivost sta dva kita, na katerih je počivala njegova posebna teorija relativnosti. Na kratko, njegovi predpogoji se lahko zmanjšajo na dve predpostavki, ki sta bili potrebni za oblikovanje novih zakonov:

1. Vsi fizikalni zakoni v inercialnih sistemih se izvajajo na enak način.
2. Hitrost svetlobe v vakuumu je konstantna, ni odvisna od lokacije opazovalca in njegove hitrosti.

Ti postulati posebne teorije relativnosti so naredili teorijo o mitskem etru neuporabna. Namesto te snovi je bil predlagan koncept štiri-dimenzionalnega prostora, ki povezuje čas in prostor. Pri določanju lokacije telesa v prostoru je treba upoštevati četrti koordinatni čas. Ta ideja se zdi precej umetna, vendar je treba opozoriti, da je potrditev tega stališča v hitrostih, ki so sorazmerne s hitrostjo svetlobe, in v vsakdanjem svetu zakoni klasične fizike opravljajo svoje delo popolnoma. Galilejsko načelo relativnosti je izpolnjen za vse inercialne referenčne okvire: če je pravilo F = ma opazljeno v CO k, bo to pravilno v drugem referenčnem okviru k '. V klasični fiziki je čas določena količina in njena vrednost je nespremenljiva in ni odvisna od gibanja inercialne FR.

Pretvorba v bencinski servis

Na kratko, koordinate točke in časa lahko označimo kot:

x '= x - vt in t' = t.

Ta formula daje klasično fiziko. Posebna teorija relativnosti ponuja to formulo v bolj zapleteni obliki.

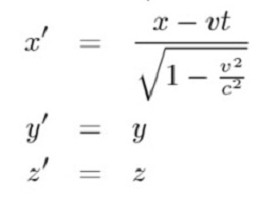
V tej enačbi količine (x, x 'y, y' z, z 't, t') označujejo koordinate objekta in pretok časa v opazovanih referenčnih sistemih, v je hitrost objekta in c je hitrost svetlobe v vakuumu.

Hitrosti predmetov v tem primeru morajo ustrezati nestandardnemu Galileju

formula v = s / t in takšna Lorentzova transformacija:

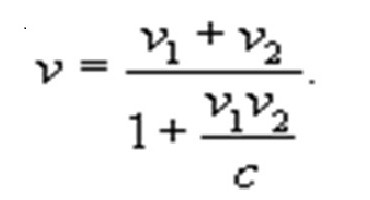
Kot je razvidno, pri zanemarljivi telesni hitrosti se te enačbe degenerirajo skozi znane enačbe klasične fizike. Če želimo drugo skrajnost in nastavimo hitrost predmeta, ki je enaka hitrosti svetlobe, potem se v tem omejevalnem primeru c še vedno doseže. Zato posebna teorija relativnosti ugotavlja, da se nobeno telo v opazovalnem svetu ne more premikati s hitrostjo, ki presega hitrost svetlobe.

Posledice SRT

Z nadaljnjim proučevanjem Lorentzovih transformacij postane jasno, da se s standardnimi objekti začnejo dogajati nestandardne stvari. Posledice posebne teorije relativnosti je sprememba dolžine predmeta in pretoka časa. Če bo dolžina segmenta v enem referenčnem okviru enaka l, bodo opažanja drugega OS dala naslednjo vrednost:

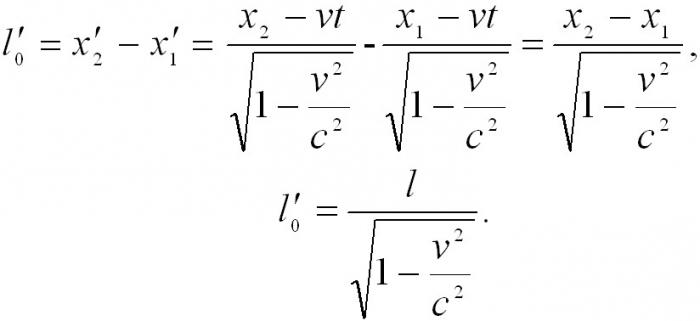
Tako se izkaže, da opazovalec iz drugega referenčnega sistema vidi segment krajši od prvega.

Osupljiva preobrazba se je dotaknila in takšne razsežnosti kot čas. Enačba za koordinato t bo izgledala takole:

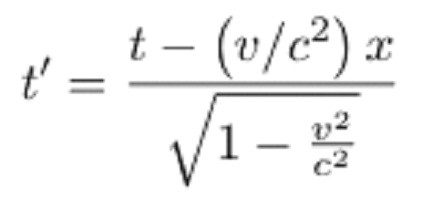
Kot lahko vidite, čas v drugem referenčnem okviru teče počasneje kot v prvem. Seveda bodo obe enačbi dali rezultate le pri hitrostih, primerljivih s hitrostjo svetlobe.

Prvi, ki izpelje formulo za časovno dilatacijo, je Einstein. Ponudil je tudi rešitev tako imenovanega "dvojnega paradoksa". Glede na pogoj te naloge so bratje dvojčici, eden od njih je ostal na Zemlji, drugi pa je odletel v vesolje na raketi. Po zgornji formuli bodo bratje starali na različne načine, saj je čas za potovalnega brata počasnejši. Ta paradoks ima rešitev, če pomislimo, da je brat-homebody vedno v inercialnem referenčnem okviru, medtem ko je dvojni fidget potoval v ne-inercialnem CO, ki se je gibal s pospeškom.

Sprememba teže

Druga posledica SRT je sprememba mase opazovanega objekta v različnih CO. Ker so vsi fizikalni zakoni enako veljavni v vseh inercialnih referenčnih sistemih, je treba upoštevati temeljne zakone ohranjanja - moment, energijo in kotni moment -. Ker pa je hitrost opazovalca v stacionarnem CO večja od hitrosti v gibljivi, potem se mora po zakonu ohranjanja gibalne mase masa predmeta spremeniti za vrednost: 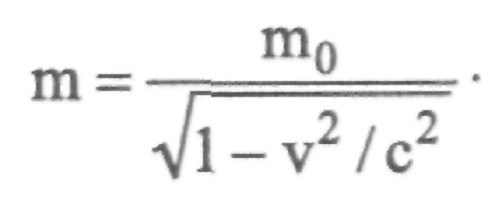V prvem referenčnem sistemu mora imeti objekt večjo telesno maso kot v drugem.

Če je hitrost telesa enaka hitrosti svetlobe, dobimo nepričakovani zaključek - masa objekta doseže neskončno vrednost. Seveda ima vsako materialno telo v opazljivem vesolju svojo končno maso. Enačba pravi le, da se noben fizični predmet ne more premikati s hitrostjo svetlobe.

Razmerje med maso in energijo

Ko je hitrost predmeta veliko nižja od hitrosti svetlobe, se enačba za maso lahko pripelje v obliko:

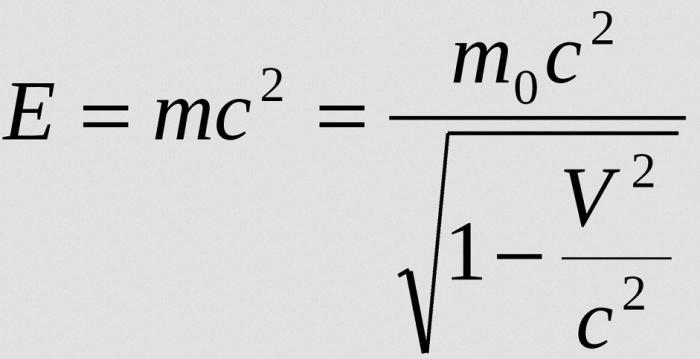
Izraz m ₀ c je neka lastnost predmeta, ki je odvisen samo od njegove mase. Ta vrednost se imenuje preostala energija. Vsota energij počitka in gibanja lahko zapišemo kot:

mc ² = m ₀ c + E _kin .

Iz tega sledi, da je skupna energija objekta lahko izražena s formulo:

E = mc ² .

Preprostost in eleganca formule telesne energije sta dali popolnost,

kjer je E skupna energija telesa.

Preprostost in eleganca znane Einsteinove formule je dala popolnost posebni teoriji relativnosti, tako da je bila notranje skladna in ni zahtevala veliko predpostavk. Tako so raziskovalci razložili številna protislovja in dali zagon za proučevanje novih naravnih pojavov.