Paralaksa je, kaj je to?

Cosmos je eden najbolj skrivnostnih konceptov na svetu. Če ponoči gledate v nebo, lahko vidite nešteto zvezd. Da, verjetno je vsak izmed nas slišal, da je v vesolju več zvezd, kot je pesek v Sahari. In znanstveniki iz antičnih časov so se raztegnili na nočno nebo in poskušali rešiti uganke, skrite za to črno praznino. Od davnih časov imajo izboljšane metode za merjenje razdalj v prostoru in lastnosti zvezdne snovi (temperatura, gostota, hitrost vrtenja). V tem članku bomo govorili o tem, kaj je paralaksa zvezd in kako jo uporabljamo v astronomiji in astrofiziki.

Pojav paralakse je tesno povezan z geometrijo, toda preden razmislimo o geometrijskih zakonih, na katerih temelji ta pojav, se bomo potopili v zgodovino astronomije in preučili, kdo in kdaj je odkril to lastnost gibanja zvezd in jo najprej uporabil v praksi.

Zgodovina

Paralaksa kot pojav spreminjanja položaja zvezd glede na lokacijo opazovalca je znana že zelo dolgo časa. Več o tem je Galileo Galileo zapisal v daljnem srednjem veku. Predvideval je samo, da če je mogoče opaziti spremembo paralakse za oddaljene zvezde, bi to dokazal Zemlja se vrti okoli sonca, in ne obratno. In res je bilo. Vendar Galileo tega ni mogel dokazati zaradi nezadostne občutljivosti takratne opreme.

Bližje našim dnem, leta 1837, je Vasily Yakovlevich Struve izvedel vrsto poskusov za merjenje letne paralakse za zvezdo Vego, ki je v ozvezdju Lyra. Kasneje so se te meritve štele za nezanesljive, ko je v letu po objavi Struveja leta 1838 Friedrich Wilhelm Bessel izmeril letno paralakso za zvezdo 61 Cygnus. Torej, ne glede na to, kako žalostna je, je prednostna naloga odprtja enoletne paralakse še vedno Bessel.

Danes se paralaksa uporablja kot glavna merilne metode razdalje do zvezd in z dovolj natančno merilno opremo daje rezultate z minimalno napako.

Morali bi iti čez geometrijo, preden se neposredno sprašujemo, kaj je paralaksa. In za začetek se spomnimo osnovnosti tega zanimivega, čeprav nezaslišanega s strani mnogih znanosti.

Osnove geometrije

Torej, kar moramo vedeti iz geometrije, da bi razumeli pojav paralakse, je, kako so koti med stranicami trikotnika in njihova dolžina povezani.

Za začetek si zamislite trikotnik. Ima tri povezovalne ravne črte in tri kote. In za vsak trikotnik - lastni koti in dolžine strani. Velikosti ene ali dveh strani trikotnika s konstantnimi vrednostmi kotov med njimi ni mogoče spremeniti, to je ena od temeljnih resnic geometrije.

Predstavljajte si, da se soočamo z nalogo, da ugotovimo vrednost dolžin obeh strani, če poznamo le dolžino osnove in velikost kotov, ki se nahajajo ob njem. To je mogoče s pomočjo ene same matematične formule, ki povezuje vrednosti dolžin stranic in vrednosti kotov, ki ležijo nasproti njima. Torej si zamislite, da imamo tri tocke (lahko vzamete svinčnik in jih narišete), ki tvorijo trikotnik: A, B, C. Oblikujejo tri strani: AB, BC, CA. Nasproti vsakega od njih leži kot: kot BCA nasproti AB, kot BAC nasproti BC, kot ABC nasproti CA.

Formula, ki povezuje vseh teh šest količin skupaj, izgleda takole:

AB / sin (BCA) = BC / sin (BAC) = CA / sin (ABC).

Kot lahko vidimo, vse ni čisto preprosto. Nekje imamo sinusni kot. Toda kako najti ta sinus? O tem vam bomo povedali spodaj.

Osnove trigonometrije

Sinus je trigonometrična funkcija, ki določa koordinato Y kota, ki je narisan na koordinatni ravnini. Da bi to jasno pokazali, običajno narišejo koordinatno ravnino z dvema osema - OX in OY - in označita točke 1 in -1 na vsaki izmed njih. Te točke se nahajajo na isti razdalji od središča ravnine, zato lahko skozi njih potegnete krog. Torej imamo tako imenovani enotni krog. Zdaj bomo zgradili nekaj segmentov z začetkom na začetku koordinat in konec na neki točki našega kroga. Konec segmenta, ki leži na krogu, ima določene koordinate na osi OX in OY. Vrednosti teh koordinat bodo kosinus in sinus.

Ugotovili smo, kaj je sinus in kako ga lahko najdete. Toda v resnici je ta metoda zgolj grafična in ustvarjena bolj za razumevanje samega bistva trigonometričnih funkcij. Učinkovit je pri kotih, ki nimajo neskončnih racionalnih vrednosti kosinusa in sinusa. Za slednje je bolj učinkovita druga metoda, ki temelji na uporabi derivatov in binomskih izračunov. To se imenuje Taylorjeva serija. Te metode ne bomo upoštevali, ker je precej zapletena za izračun. Konec koncev je hitro računalništvo delo za računalnike, ki so namenjeni temu. Serija Taylor se uporablja v kalkulatorjih za izračun številnih funkcij, vključno s sinusom, kosinusom, logaritmom in tako naprej.

Vse to je precej zanimivo in zasvojenost, vendar je čas, da gremo naprej in se vrnemo tja, kjer smo se končali: na računu vrednosti neznanih strani trikotnika.

Strani trikotnika

Torej, nazaj na naš problem: poznamo dva kota in stran trikotnika, na katera so ti koti sosednji. Vedeti moramo samo en vogal in dve strani. Zdi se, da je iskanje kota najlažje: vsota vseh treh vogalov trikotnika je 180 stopinj, kar pomeni, da lahko zlahka najdete tretji kot, tako da odštejete vrednosti dveh znanih kotov od 180 stopinj. In če poznamo vrednosti vseh treh kotov in ene od strani, lahko najdemo dolžine dveh drugih strani. Sami lahko preverite na primeru katerega koli trikotnika.

In zdaj končno govorimo o paralaksi kot načinu za merjenje razdalje med zvezdami.

Paralaksa

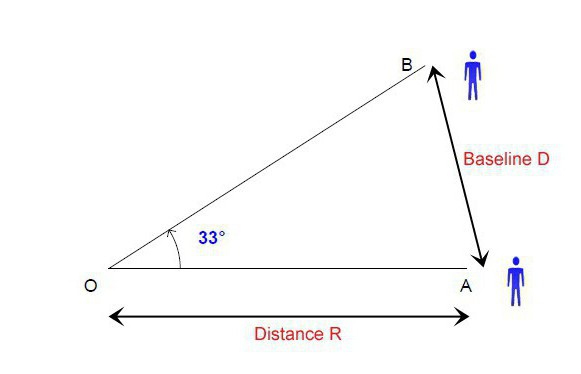
To je, kot smo že ugotovili, ena najpreprostejših in najučinkovitejših metod za merjenje medzvezdnih razdalj. Paralaksa temelji na spreminjanju položaja zvezde glede na njegovo razdaljo. Na primer, z merjenjem kota navideznega položaja zvezde na eni tocki orbite, nato pa neposredno na njej, dobimo trikotnik, v katerem sta znani dolžina ene strani (razdalja med nasprotnima tockama orbite) in dva kota. Od tu bomo lahko našli dve preostali strani, od katerih je vsaka enaka razdalji od zvezde do našega planeta na različnih točkah njegove orbite. To je metoda, s katero lahko izračunamo paralakso zvezd. In ne samo zvezde. Paralaksa, katere učinek je kljub temu zelo preprost, se v mnogih različicah uporablja v popolnoma različnih področjih.

V naslednjih razdelkih si bomo podrobneje ogledali področje paralakse.

Kozmos

O tem smo večkrat govorili, saj je paralaksa izjemen izum astronomov, zasnovan za merjenje razdalj do zvezd in drugih vesoljskih objektov. Vendar to ni tako preprosto. Navsezadnje je paralaksa metoda, ki ima svoje različice. Na primer, razlikujejo se dnevne, letne in starodavne paralakse. Lahko sklepamo, da se vsi razlikujejo v časovnem intervalu, ki poteka med merilnimi koraki. Ni mogoče reči, da povečanje časovnega intervala poveča natančnost merjenja, ker so cilji vsake vrste te metode različni, natančnost merjenja pa je odvisna samo od občutljivosti opreme in izbrane razdalje.

Dnevna paralaksa

Dnevna paralaksa, razdalja, s katero je določen kot med črtama, ki gredo do zvezde, iz dveh različnih točk: središče Zemlje in izbrana točka na Zemlji. Ker poznamo polmer našega planeta, ni težko s pomočjo kotne paralakse izračunati razdaljo do zvezde z uporabo matematične metode, ki smo jo opisali prej. V bistvu se dnevna paralaksa uporablja za merjenje blizu objektov, kot je npr planeti, pritlikavi planeti ali asteroidov. Za večje uporabite naslednjo metodo.

Eno leto paralaksa

Enoletna paralaksa je še vedno ista metoda merjenja razdalj z edino razliko, da se osredotoča na merjenje razdalj do zvezd. To je ravno primer paralakse, ki smo jo upoštevali v zgornjem primeru. Paralaksa, ki določa razdaljo do zvezde, s pomočjo katere je lahko zelo natančna, mora imeti eno pomembno značilnost: razdalja, od katere se meri paralaksa, mora biti večja, to bolje. Enoletna paralaksa izpolnjuje ta pogoj: navsezadnje je razdalja med skrajnimi točkami orbite precej velika.

Paralaksa, primeri metod, ki smo jih obravnavali, je vsekakor pomemben del astronomije in služi kot nepogrešljivo orodje pri merjenju razdalje do zvezd. Pravzaprav je danes uporabljena le enoletna paralaksa, saj se lahko dnevna zamenja z naprednejšo in hitrejšo eholokacijo.

Pojdi naprej. Paralaksa je še vedno optični pojav in bilo bi čudno, če bi se njene lastnosti uporabljale le v astronomiji. Obstaja še eno področje uporabe tega učinka.

Fotografija

Morda je najbolj znana vrsta fotografske paralakse lahko binokularna paralaksa. Verjetno ste to sami opazili. Če prinesete prst na oči in zaprete vsako oko, boste opazili, da se spreminja vidni kot objekta. Enako se zgodi pri fotografiranju blizu objektov. V objektivu vidimo sliko iz enega kota, v resnici pa bo fotografija izšla z nekoliko drugačnim kotom, saj obstaja razlika v razdalji med objektivom in iskalom (luknja, skozi katero gledamo fotografijo).

Preden končamo ta članek - nekaj besed o tem, kako je lahko uporaben tak pojav, kot je optična paralaksa, in zakaj bi se morali o tem več naučiti.

Zakaj je to zanimivo?

Za začetek je paralaksa edinstven fizični fenomen, ki nam omogoča, da se veliko naučimo o svetu okoli nas in celo o tem, kaj je na stotine svetlobnih let od njega: po vsem, s pomočjo tega pojava je mogoče izračunati velikosti zvezd.

Kot smo že videli, paralaksa ni tako oddaljen pojav od nas, nas obdaja povsod in s pomočjo tega vidimo, kot je. To je vsekakor zanimivo in razburljivo, zato je treba paziti na metodo paralakse, čeprav samo iz radovednosti. Znanje ni nikoli odveč.

Zaključek

Zato smo analizirali, kaj je bistvo paralakse, zakaj določanje razdalje do zvezd ni potrebno imeti zapleteno opremo, ampak samo teleskop in poznavanje geometrije, kako se uporablja v našem telesu in zakaj smo tako pomembni v vsakdanjem življenju. Upamo, da so vam informacije bile koristne!