Kinetična energija - energija gibanja teles
Potencialna in kinetična energija nam omogočata, da opišemo stanje vsakega telesa. Če se prvi uporablja v sistemih medsebojno delujočih predmetov, potem je slednji povezan z njihovim gibanjem. Te vrste energije se praviloma upoštevajo, ko sila, ki povezuje telesa, ni odvisna od poti gibanja. V tem primeru so pomembni samo začetni in končni položaji.
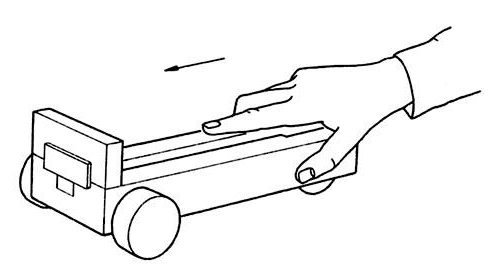
Splošne informacije in koncepti
Kinetična energija sistema je ena njegovih najpomembnejših značilnosti. Fiziki razlikujejo dve vrsti energije, odvisno od vrste gibanja:
• progresivno;
• rotacija.
Kinetična energija (E k ) je razlika med celotno energijo sistema in ostalo energijo. Na podlagi tega lahko rečemo, da je to posledica gibanja sistema. Telo ima samo, ko se premika. V mirovanju je objekt nič. Kinetična energija vseh teles je odvisna samo od hitrosti gibanja in njihove mase. Celotna energija sistema je neposredno odvisna od hitrosti njenih objektov in razdalje med njimi.
Osnovne formule
V primeru, da vsaka sila (F) deluje na telo, ki je v mirovanju na tak način, da se začne gibati, lahko govorimo o opravljanju dela dA. Vrednost te energije dE bo višja, več dela bo opravljenega. V tem primeru velja naslednja enakost: dA = dE.
Glede na pot, ki jo prevaža telo (dR) in njena hitrost (dU), lahko uporabimo 2 Newtonov zakon, na podlagi katerega: F = (dU / dE) * m.
Zgoraj navedeni zakon se uporablja samo, če obstaja inertni referenčni sistem. Obstaja še en pomemben odtenek, ki se upošteva pri izračunih. Na vrednost energije vpliva izbira sistema. Torej se po sistemu SI meri v joulih (J). Kinetično energijo telesa označuje masa m in hitrost gibanja υ. V tem primeru bo to: E k = ((υ * υ) * m) / 2.
Na podlagi zgornje formule lahko sklepamo, da je kinetična energija določena z maso in hitrostjo. Z drugimi besedami, to je funkcija gibanja telesa.
Energija v mehanskem sistemu
 Kinetična energija je mehanska energija sistema. Odvisna je od hitrosti njenih točk. Glede na energijo materialne točke je predstavljena z naslednjo formulo: E = 1 / 2mυ 2, kjer je m masa točke, in υ je njena hitrost.
Kinetična energija je mehanska energija sistema. Odvisna je od hitrosti njenih točk. Glede na energijo materialne točke je predstavljena z naslednjo formulo: E = 1 / 2mυ 2, kjer je m masa točke, in υ je njena hitrost.
Kinetična energija mehanskega sistema je aritmetična vsota istih energij vseh njenih točk. Lahko se izrazi tudi z naslednjo formulo: E k = 1 / 2Mυ c2 + Ec, kjer je υc hitrost središča mase, M masa sistema, Ec je kinetična energija sistema pri gibanju okoli središča mase.
Trdna energija
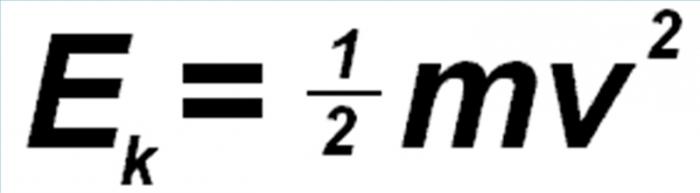 Kinetična energija telesa, ki se giblje progresivno, je določena z enako energijo točke, katere masa je enaka masi celotnega telesa. Za izračun kazalnikov pri premikanju uporabite zapletene formule. Sprememba te energije sistema v trenutku njenega premikanja iz enega položaja v drugega poteka pod vplivom uporabljenih notranjih in zunanjih sil. Je enaka vsoti dela Aue in A'u teh sil med tem gibanjem: E2 - E1 = Au Aue + ∑u A'u.
Kinetična energija telesa, ki se giblje progresivno, je določena z enako energijo točke, katere masa je enaka masi celotnega telesa. Za izračun kazalnikov pri premikanju uporabite zapletene formule. Sprememba te energije sistema v trenutku njenega premikanja iz enega položaja v drugega poteka pod vplivom uporabljenih notranjih in zunanjih sil. Je enaka vsoti dela Aue in A'u teh sil med tem gibanjem: E2 - E1 = Au Aue + ∑u A'u.
Ta enakost odraža izrek o spremembi kinetične energije. Z njegovo pomočjo se rešujejo različni problemi mehanike. Brez te formule ni mogoče rešiti več pomembnih nalog.
Kinetična energija pri visokih hitrostih
Če je hitrost telesa blizu hitrosti svetlobe, se kinetična energija materialne točke lahko izračuna po naslednji formuli:
E = m0c2 / -1-υ2 / c2 - m0c2,
kjer je c hitrost svetlobe v vakuumu, je m0 masa točke, m0c2 je energija točke. Pri nizki hitrosti (υ Med vrtenjem telesa okrog osi vsak od osnovnih elementov mase (mi) opisuje krog polmera ri. Na tej točki ima volumen linearno hitrost υi. Ker se šteje trdna snov, kotna hitrost rotacija vseh volumnov bo enaka: ω = υ1 / r1 = υ2 / r2 = ... = υn / rn (1). Kinetična energija vrtenja trdne snovi je vsota vseh enakih energij njenih osnovnih volumnov: E = m1υ1 2/2 + miυi 2/2 + ... + mnυn 2/2 (2). Pri uporabi izraza (1) dobimo formulo: E = Jz ω 2/2, kjer je Jz trenutek vztrajnosti telesa okoli osi Z. Pri primerjavi vseh formul postane jasno, da je vztrajnostni moment merilo telesne inercije med rotacijsko gibanje. Formula (2) je primerna za objekte, ki se vrtijo okoli fiksne osi. Kinetična energija telesa, ki se giblje po ravnini, je sestavljena iz energije vrtenja in translacijskega gibanja: E = mυc2 / 2 + Jz ω 2/2, kjer je m masa gibljivega telesa, Jz je moment vztrajnosti telesa okrog osi, υc je hitrost središča mase, ω je kotna hitrost. Sprememba vrednosti kinetične energije je tesno povezana s potencialom. Bistvo tega pojava je mogoče razumeti skozi zakon ohranjanja energije v sistemu. Vsota E + dP med gibanjem telesa bo vedno enaka. Sprememba vrednosti E se vedno pojavi hkrati s spremembo dP. Tako se preoblikujejo, kot da tečejo drug v drugega. Takšen pojav lahko najdemo v skoraj vseh mehanskih sistemih. Za izračun energijske vrednosti izberemo poljuben trenutek (velja za začetni) in referenčni sistem. Točno količino potencialne energije je mogoče določiti le v območju vpliva sil, ki pri delu niso odvisne od poti telesa. V fiziki se te sile imenujejo konzervativne. Imajo stalno povezavo z zakonom ohranjanja energije. Če je zunanji vpliv minimalen ali zmanjšan na nič, bo sistem, ki ga bomo proučevali, vedno v stanju, v katerem bo njegova potencialna energija prav tako naravnana na nič. Na primer, vržena žoga bo dosegla mejo te energije na zgornji točki poti gibanja in v istem trenutku se bo začela spuščati. V tem času se akumulirana energija v letu pretvori v gibanje (opravljeno delo). Za potencialno energijo, v vsakem primeru, obstaja interakcija vsaj dveh teles (v primeru z žogo, na katero vpliva gravitacija planeta). Kinetična energija se lahko izračuna individualno za katero koli premično telo. Potencialna in kinetična energija se spreminjata izključno v interakciji teles, ko sila, ki deluje na telo, opravlja delo, katerega vrednost se razlikuje od nič. V zaprtem sistemu je delo sile ali elastičnosti enako spremembi potencialne energije predmetov z znakom "-": A = - (Ep2 - Ep1). Delo sile ali elastičnosti je enako spremembi energije: A = Ek2 - Ek1. Iz primerjave obeh enačb je razvidno, da je sprememba energije objektov v zaprtem sistemu enaka spremembi potencialne energije in je nasprotna v znaku: Ek2 - Ek1 = - (Ep2 - Ep1) ali drugače: Ek1 + Ep1 = Ek2 + Ep2. Iz te enakosti je jasno, da vsota teh dveh energij teles v zaprtem mehanskem sistemu in vzajemno delujočih sil elastičnosti in agresije vedno ostane konstantna. Na podlagi navedenega lahko sklepamo, da je treba v procesu proučevanja mehanskega sistema upoštevati interakcijo potencialnih in kinetičnih energij. 
Rotacijska energija sistema
Planarno gibanje telesa

Sprememba energije v mehanskem sistemu
Energetska povezava
Potencialne in kinetične energije so tesno povezane. Njihovo vsoto lahko predstavimo kot skupno energijo sistema. Na molekularni ravni je notranje energije telo. Prisotna je nenehno, dokler obstaja vsaj nekaj medsebojnega delovanja telesa in toplotnega gibanja. Izbira referenčnega sistema
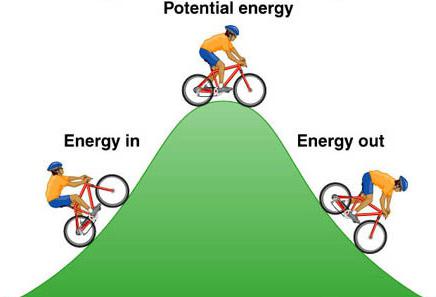
Bistvo razlike med potencialno in kinetično energijo
Povezovanje različnih energij