Kako najti stran trikotnika - pomagati učencu

Obstaja več načinov za reševanje tega geometrijskega problema. Opisani so v članku.

S stranicami in vogali

Prvi način, kako najti stranice trikotnika, je na več straneh in kot med njimi (in podobno kot z vogali in sosednjo stranjo). Ta metoda je primerna za srednjo šolo, saj uporablja koncepte, kot so sinus, kosinus, kvadratna številka in koren. Torej, kako najti stran trikotnika, ki je poljuben? Za začetek, narišite to sliko. Zdaj pa pokličimo elemente naše figure. Stranki bosta a, b in c. Kot, ki se nahaja nasproti strani a, bomo imeli alfa, nasproti b - beta, nasproti c - gama. 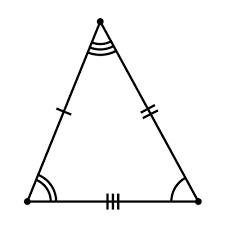Da bi našli stran, recimo, a, morate izračunati kvadratni koren od vsote kvadrata b, c in od nje odštejemo dvojni produkt kosinusa kota a na straneh b in c. Da bi olajšali obliko formule in razložili, kako najti stran trikotnika poljubne oblike, lahko zapišemo naslednje: a = (b * b + c * c-2 * b * c * cos "alfa") ^ (1 / 2). Bodite previdni, ker, če je kot nasproti želene strani top, potem bo kosinus zavzel negativno vrednost. Druga formula za iskanje strani trikotnika je na dveh vogalih in na straneh. Takoj podajamo formulo-enakost, saj je za razumevanje vizualna oblika enostavnejša kot dolga slika. Še vedno moramo najti stran a. Potem, na podlagi zapisa, dobimo naslednje: a = (b * sin "alpha") / sin "beta" = (b * sin "alfa") / sin ("alfa" + "gama") = (b * sin ( "beta" + "gama")) / sin "beta". To je težaven način za iskanje neznane strani poljubnega trikotnika.

Enakokraki trikotnik

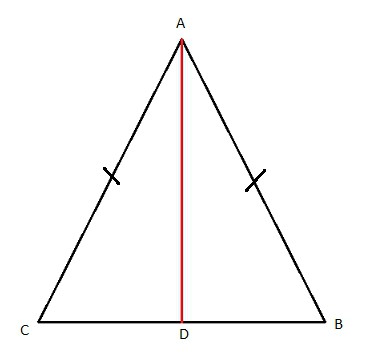
Kaj je enakokračni trikotnik? Samo po sebi ima dve identični strani in tako imenovano osnovo. Dvojne stranice so označene s črko a, baza - b. Torej, ker ima trikotnik dva »boka« enake velikosti, bodo tudi koti na »temelje« enaki. Naj jim rečemo alfa. Da bi odgovorili, kako najti stran enakokrakega trikotnika, morate vnesti drugo vrednost - kot med enakimi "boki".
Ker se nahaja nasproti b, je najbolje, da jo imenujemo "beta". Pri iskanju neznanih strani lahko uporabite več formul. Poglejmo, katere. Prva dva sta tista, s katerimi lahko izračunamo dolžino stranice osnove enakokrakega trikotnika. Temelji na znanju študentov o sinusih in kosinusih. 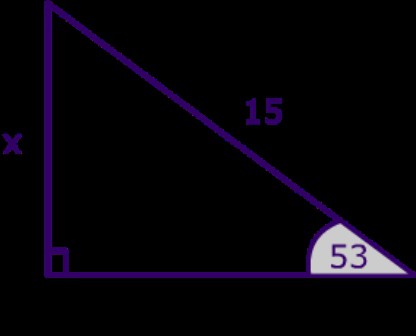Torej, naši izračuni izgledajo takole: b = 2 * a * sin ("beta" / 2) = a * (2-2 * cos "beta") ^ (1/2) ali b = 2 * a * cos alfa. Enostavno in enostavno. Še posebej, če "dobite roko" in vadite. Zdaj lahko pogledamo, kako izračunati dolžino enakih strani. Tudi tu sta dve možnosti, ki sta malo bolj zapleteni kot prejšnji. Izgledajo okorne, vendar vas ne bi smelo prestrašiti. Kako najti "boke"? Imeli bomo naslednje formule: a = b / (2 * sin ("beta" / 2)) = b / (2-2 * cos "beta") ^ (1/2) ali a = b / (2 / cos "alfa"). Kateri zapis naj uporabim? Vse je odvisno od naloge in pogojev. Seveda lahko preračunate za vse formule, če imate absolutno vse podatke. Zdaj lahko gremo naprej.

Desni trikotnik

Verjetno vsak učenec, ki je pravkar začel študirati geometrijo, ve kaj pravokotni trikotnik. Na prvi pogled ta podatek ni nič posebnega, kompleksnega in nerazumljivega. Toda ko se problemi izgubijo glede ene ali druge strani tega geometrijskega objekta, se začnejo težave. Stvar je v tem, da vprašanje: "Kako najti stran pravokotnega trikotnika?" - ne vpliva samo na koncepte sinusnega in kosinusnega, ampak tudi na tangente kotov. Tako so izračuni postali veliko bolj zapleteni in še več. Torej najprej označimo dve nogi narisanega pravokotnega trikotnika z a in b. Koti, ki ležijo nasproti tem stranicam, kot je bilo običajno prej, se imenujejo alfa in beta. Naša hipotenuza bo stran c. Ne potrebujemo kota, ki leži proti njej - bo naravnost. Obstaja več različic izračunov. Prva se imenuje klasična. Za nogo a so formule videti: a = c * cos "beta" = c * sin "alpha" = b * tg "alfa".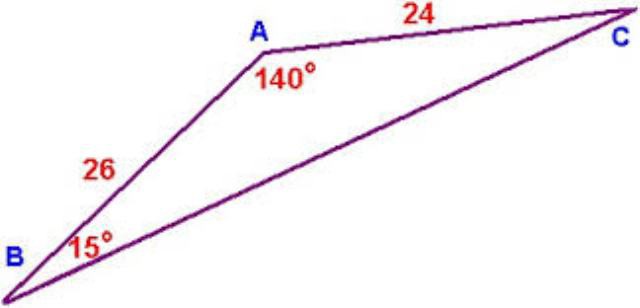
Na podoben način najdemo stran b: b = c * cos "alpha" = c * sin "beta" = a * tg "beta". Nato najdemo našo hipotenuzo s: c = a / sin "alpha" = a / cos "beta" ali c = b / cos "alfa" = b / sin "beta". Druga, enostavnejša in bolj znana metoda iskanja strani pravokotnega trikotnika je v skladu s Pitagorovim izrekom. Piše: vsota kvadratov obeh nog je enaka kvadratu hipotenuze. Torej bomo imeli naslednje: a = (c * cb * b) ^ (1/2), b = (c * ca * a) ^ (1/2), c = (b * b + a * a) ^ (1/2). Tukaj je preprost in preprost odgovor na vprašanje, kako najti stran trikotnika. Ne bojte se ogromnih izračunov.

Rezultati

Tako smo danes ugotovili, kako najti stran trikotnika in se naučili veliko novih formul. Da bi jih bolje zapomnili, jih zapišite na nek kos papirja, na katerem bo kasneje lažje vse naučiti na pamet. Ne bojte se "strašnih" številk in velikih izračunov. Vse je lažje, kot se zdi.