Kako izračunati obseg žoge in druge nianse v izračunih

Preden začnete preučevati pojem krogle, kolikšen je obseg krogle, razmislite o formulah za izračunavanje njenih parametrov, morate se spomniti koncepta kroga, ki smo ga raziskali že v času geometrije. Konec koncev je večina dejanj v tridimenzionalni prostor so podobne ali izhajajo iz dvodimenzionalne geometrije, popravljene za videz tretje koordinate in tretje stopnje.

Kaj je krog?

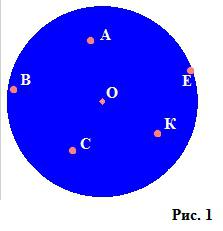
Krog je številka na kartezični ravnini (prikazana na sliki 1); Najpogosteje se definicija sliši kot "lokus vseh točk na ravnini, razdalja, od katere do določene točke (središče) ne presega določenega ne-negativnega števila, imenovanega polmer."

Kot vidimo na sliki, je točka O središče slike in množica absolutno vseh točk, ki zapolnjujejo krog, na primer A, B, C, K, E, ne presegajo določenega polmera (ne presegajo kroga, prikazanega na sliki) 2).

Če je polmer nič, potem se krog spremeni v točko.

Razumevanje težav

Učenci pogosto zamenjujejo te koncepte. Enostavno si ga lahko zapomnimo, če naredimo analogijo. Obroč, ki ga otroci prepletajo v razredih telesne vzgoje, je krog. Če razumemo to ali se spomnimo, da so prve črke obeh besed »O«, bodo otroci razumljivo razliko razumeli.

Predstavitev koncepta "žogice"

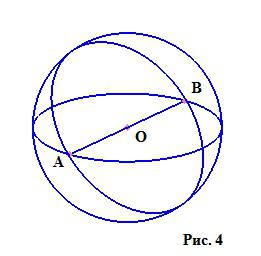
Krogla je telo (sl. 3), omejeno s sferično površino. Kakšna »sferična površina« bo postala jasna iz njegove definicije: to je geometrijska lokacija vseh točk na površini, razdalja, od katere do določene točke (središče) ne presega določenega ne-negativnega števila, imenovanega polmer. Kot vidimo, sta pojma kroga in sferične površine podobna, le prostori, v katerih se nahajajo, se razlikujejo. Če v dvodimenzionalnem prostoru narišemo kroglo, dobimo krog, katerega meja je krog (na krogli je kroglasta površina). Na sliki vidimo sferično površino s polmeri OA = OB.

Žoga je zaprta in odprta

V vektorskih in metričnih prostorih sta upoštevana tudi dva pojma, povezana s sferično površino. Če žogica vključuje samo to sfero, se imenuje zaprta, če pa ni, potem je žoga odprta. To so bolj »napredni« koncepti, ki jih preučujemo v institucijah z uvodom v analizo. Za preprosto in celo uporabo v gospodinjstvu zadostujejo tiste formule, ki se preučujejo v stereometriji 10–11 razredov. Takšni koncepti so dostopni skoraj vsakemu povprečnemu izobražencu, o katerem bomo še razpravljali.

Koncepti, ki jih morate poznati za naslednje izračune

- polmer in premer.

- Polmer krogle in njen premer se določita na enak način kot krog.

- Radius - segment, ki povezuje katero koli točko na meji žoge in točko, ki je središče žoge.

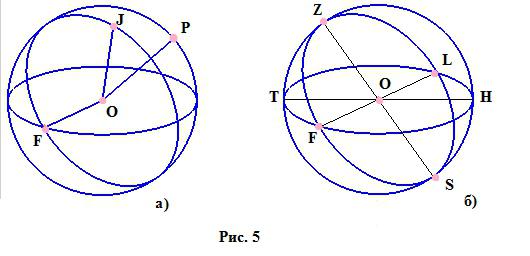
- Premer - segment, ki povezuje dve točki na robu krogle in poteka skozi njegovo središče. Slika 5a jasno kaže, kateri segmenti so polmeri krogle, na sliki 5b pa so prikazani premeri krogle (segmenti, ki prehajajo skozi točko O).

Odseki na področju (krogla)

Vsak del krogle je krog. Če gre skozi središče krogle, se imenuje velik krog (krog s premerom AB), preostali deli pa so majhni krogi (krog s premerom DC).

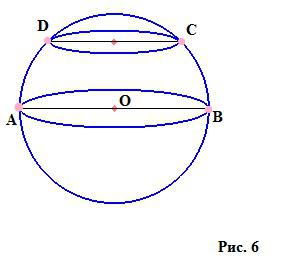
Območje teh krogov se izračuna po naslednjih formulah:

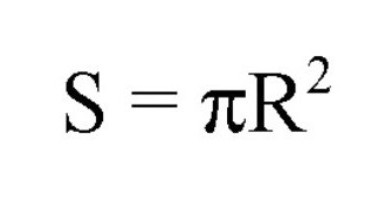
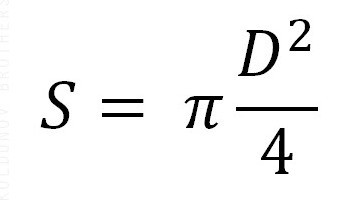
Tu je S oznaka območja, R je polmer, D premer. Prisotna je tudi konstanta 3,14. Vendar ne smemo zamenjevati, da za izračun površine velikega kroga z uporabo polmera ali premera krogle (krogle) in za določitev območja potrebujemo dimenzije polmera samo za majhen krog.

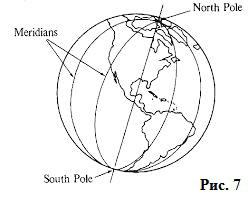
Obstaja nešteto takih odsekov, ki prečkajo dve točki istega premera, ki ležita na meji žoge. Kot primer - naš planet: dve točki na severnem in južnem polu, ki sta konca zemeljske osi, v geometrijskem smislu - konci premera in poldnevniki, ki tečejo skozi ti dve točki (slika 7). To pomeni, da se število velikih krogov v krogli nagiba k neskončnosti v številu.

Kroglični deli

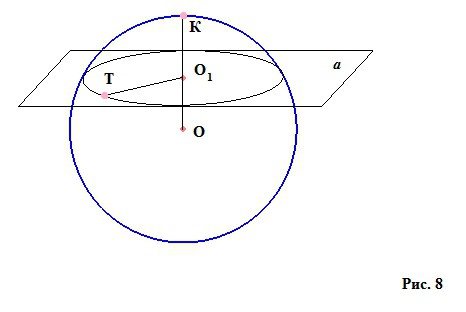
Če odrežemo kroglo iz krogle s pomočjo določene »kosovne« ravnine (slika 8), jo bomo imenovali sferični ali sferični segment. Ima višino - pravokotno od središča rezalne ravnine do sferične površine O ₁ K. Točka K na sferični površini, na katero prihaja višina, se imenuje vozlišče sferičnega segmenta. In majhen krog s polmerom O ₁ T (v tem primeru, glede na sliko, ravnina ni šla skozi središče krogle, če pa prečka središče skozi središče, potem bo krog prereza velik) nastal, ko je odsek krogle, se imenuje osnova našega kosa. krogla - sferični segment.

Če povežemo vsako točko podnožja sferičnega segmenta s središčem krogle, dobimo obliko, imenovano "krogelni sektor".

Če skozi kroglo potekajo dve ravnini, ki sta vzporedni drug z drugim, potem se tisti del krogle, ki je med njimi obdan, imenuje sferični sloj (slika 9, ki prikazuje kroglo z dvema ravninama in ločeno sferično plast).

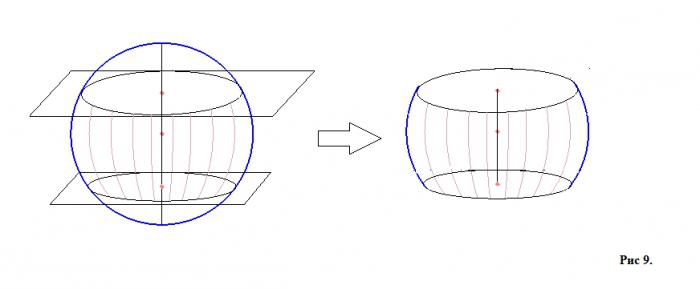
Površina (osvetljeni del na sliki 9 desno) tega dela krogle se imenuje pas (spet, za boljše razumevanje je mogoče z globusom narisati analogijo, in sicer s svojimi podnebnimi območji - arktičnimi, tropskimi, zmernimi itd.), Odseki pa bodo osnova. plast. Višina plasti je del premera, ki je pravokoten na ravnine rezanja od središč baz. Obstaja tudi koncept sfere. Oblikuje se v primeru, ko ravnine, ki so vzporedne druga z drugo, ne sekajo krogle, ampak jo dotaknejo v eni točki.

Formula za izračun prostornine krogle in njene površine

Kroglo se oblikuje z vrtenjem okoli fiksnega premera polkroga ali kroga. Za izračun različnih parametrov tega objekta ne bo potrebno preveč podatkov.

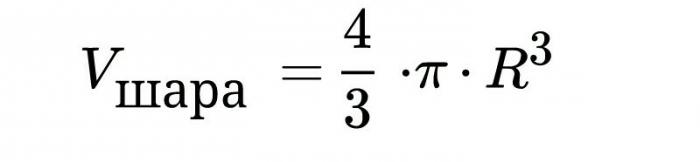
Volumen krogle, formula za izračun, ki je navedena zgoraj, je izpeljana s pomočjo integracije. Razumeli bomo točke.

Razmišljamo o krogu v dvodimenzionalni ravnini, ker, kot je omenjeno zgoraj, je krog tisti, ki tvori osnovo konstrukcije krogle. Uporabljamo le njegov četrti del (slika 10).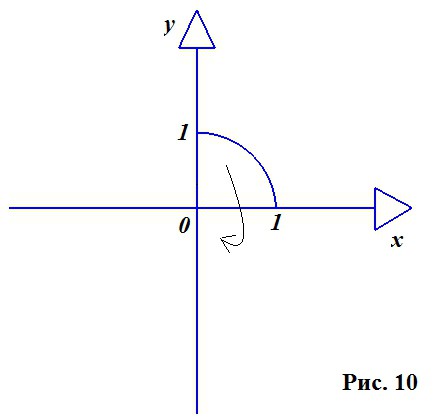

Vzemite krog s polmerom enote in sredino na začetku. Enačba takšnega kroga je naslednja: X ² + Y ² = R ² . Tukaj izrazimo Y: Y ² = R ² - X ² .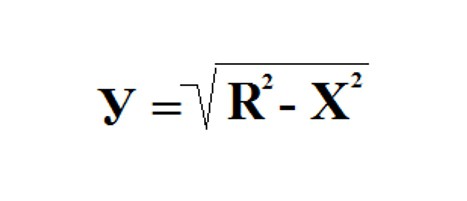

Upoštevajte, da je nastala funkcija na segmentu X (0; R) negativna, neprekinjena in padajoča, saj vrednost X v primeru, ko upoštevamo četrtino kroga, leži od nič do vrednosti polmera, to je do enega.

Naslednja stvar je, da zavrtimo četrtino kroga okoli osi x. Zato dobimo poloblo. Za določitev njegovega obsega se zatekamo k metodam integracije.

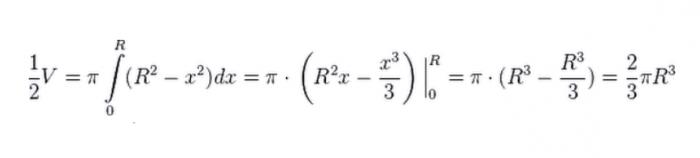
Ker je ta volumen le polobla, podvojimo rezultat, od koder dobimo, da je volumen kroglice enak:

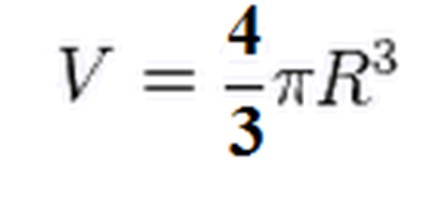
Majhne nianse

Če je potrebno izmeriti prostornino kroglice skozi njen premer, se spomnite, da je polmer polovice premera in to vrednost nadomestite z zgornjo formulo.

Prav tako je mogoče doseči formulo za prostornino krogle skozi območje njene mejne površine - kroglo. Spomnimo se, da je območje krogle izračunano s formulo S = 4πr ² , ki združuje to, prav tako pride do zgornje formule za volumen krogle. Iz enakih formul lahko izrazimo polmer, če pogoj problema vsebuje vrednost prostornine.