Kako zgraditi graf linearne funkcije. Primeri
Da bi ugotovili, kako načrtovati linearno funkcijo, je pomembno razumeti bistvo funkcije. Funkcija je model odvisnosti sprememb enega parametra od drugega.
Tema funkcionalnih odvisnosti se tradicionalno odpre z linearno funkcionalno odvisnostjo. Linearna je najpreprostejša odvisnost. Graf linearne funkcije je raven.
Življenje in funkcija
V življenju se linearne odvisnosti običajno nahajajo v idealnih umetnih procesih, pri katerih se domneva, da so spremembe trajne. Na primer, ko nekdo gre nekam s konstantno hitrostjo.
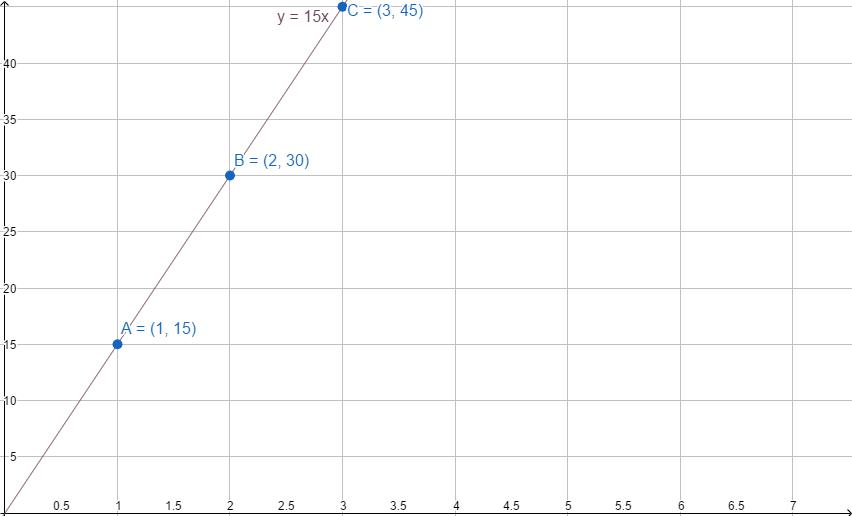
Razdalja, do katere bo oseba potovala s kolesom, se bo linearno razlikovala glede na število ur, ki jih potuje. Če vozi 15 kilometrov v eni uri (točka A), bo v dveh urah vozil 30 kilometrov (točka B), v treh urah - 45 (točka C).
Odvisnost je opisana z enačbo y = 15x. Kako načrtovati linearno funkcijo v tem primeru?
- poiščite koordinate točk, ki so rešitev enačbe;
- zgradite jih na koordinatni ravnini;
- te točke povežite z linijo.
Opis algoritma
Iskanje koordinat točk, ki so rešitve enačbe, se zniža na iskanje dveh točk, ki enolično določajo črto. Čeprav zadostuje, da izberemo dve različni vrednosti x in najdemo ustrezne vrednosti y, lahko najdemo tri pare vrednosti za samopreverjanje. Tako boste lahko hitro ugotovili morebitne napake v izračunih. Pogosto je prva vrednost x izbrana kot nič.
| y = 15x | (0, 0) | (1, 15) |
| x = 0 | x = 1 | |
| y = 15 × 0 | y = 15 × 1 | |
| y = 0 | y = 15 |
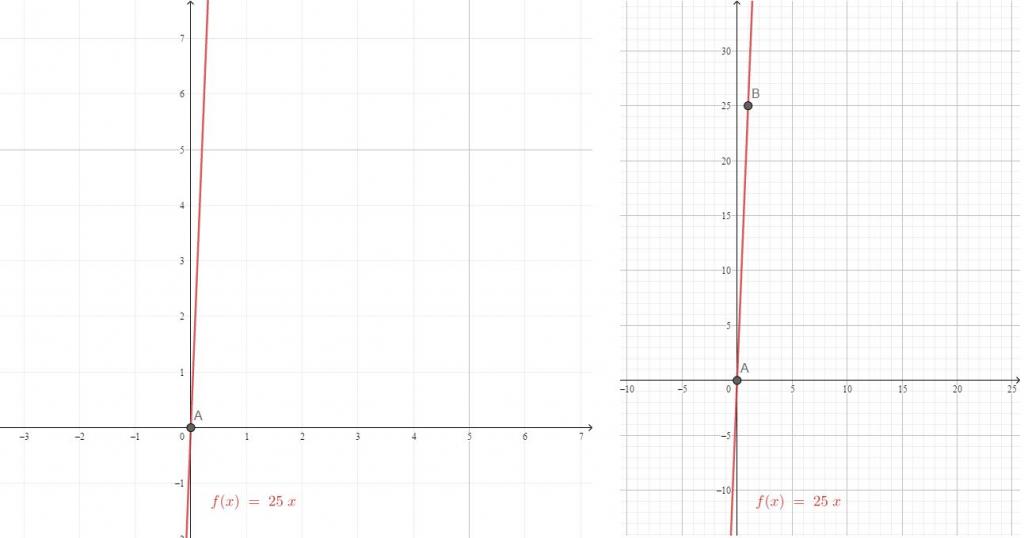
Druga vrednost x za večje k je bolje izbrati poleg prve. V nasprotnem primeru bo prisoten močan raztros v vrednostih y in x, na primer pri x = 4 v obravnavani enačbi, y = 60. V vsakem primeru je pred načrtovanjem linearne funkcije na najdenih točkah izbrana skala.
| y = 25 x | (0, 0) | (1, 25) |
| x = 0 | x = 1 | |
| y = 25 × 0 | y = 25 × 1 | |
| y = 0 | y = 25 |
Koeficient za x
Enačba linearne funkcije je oblike y = kx + b. Glede na spremembo koeficienta za neznano se spreminja tudi narava grafa linearne funkcije y = kx.
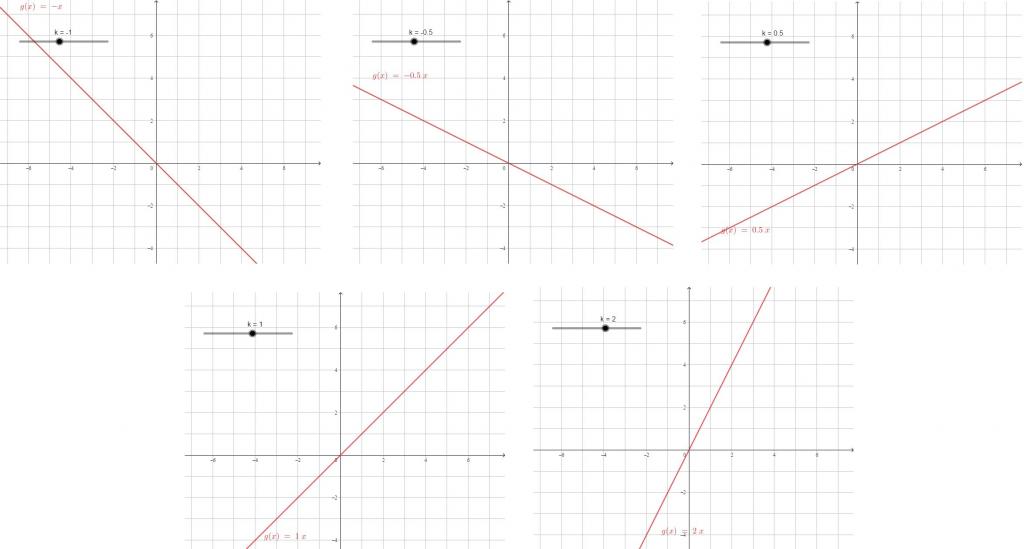
Večji koeficient modula, večja je strmina ravne črte, večja je za isto spremembo vrednosti x vrednosti y spremembe. Koeficient x je koeficient sorazmernosti.
Prosto razmerje
Prosti koeficient je konstanta, ki ni odvisna od sprememb vrednosti x. Prikazuje, kje se črta seka OY.
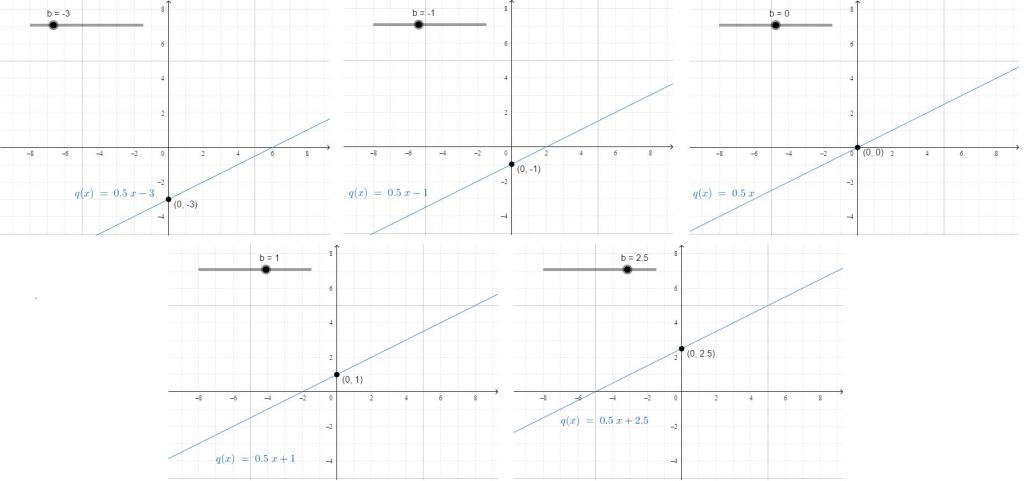
Na primer, oseba je hodila 10 kilometrov od jutra do 12 ure popoldneva, nato pa je tri ure jahala na kolesu. Potem je razdalja, ki jo je zajel dan: y = 15 × 3 + 10. Če želite izpeljati formulo za izračun razdalje na koncu vsake ure od treh, ki jih je vozil na kolesu, lahko uporabite: y = 15x + 10. Ob eni uri dan je odpeljal 15 × 1 in še 10 minilo, ob dveh je odpeljal 15 × 2, a je vseeno prešel 10.
Graf linearne funkcije y = kx + b opisuje črto, ki ima naklon k in seka OY na točki s koordinatami (0, b). Analiza enačbe vam pogosto omogoča reševanje problemov brez izdelave grafa. Da bi delovali v mislih, morajo biti dejanja dobro vezana na vizualni material.
Naloga je na primer najti presečišče y = - x 2 in y = 0.5x + 5. Prva funkcija se zmanjšuje, druga se povečuje, prva je pod drugo, ker so veje parabole navzdol in je njegova točka na izvoru. Linearna funkcija bi morala imeti veliko večji nagibni kot, da bi bila bolj strma in prečkala eno od vej parabole. Zato je mogoče nedvoumno ugotoviti, da ni križišč brez konstruiranja grafa in brez zamenjave.
Posebni primeri
- Kadar ni prostega koeficienta, je (dejansko) enaka nič, kar pomeni, da se premica premika z OY na nič.
- Če ni neznanega x ali y, sta y in x neodvisna drug od drugega. Na primer, y = 5. Ne glede na to, katera vrednost x vzame, bo y vedno 5. Grafično je to lahko predstavljeno kot ravna črta, vzporedna z OX.
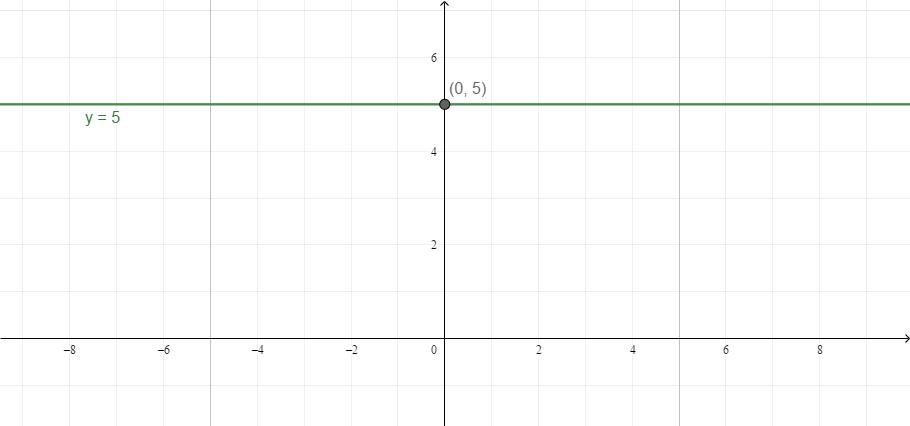
- Enako velja za primer, ko je spremenljivka x enaka številki: spremenljivka x ima konstantno vrednost.
Z analiziranjem enačbe, še preden narišemo linearno funkcijo, lahko ugotovimo njeno približno lokacijo na OY in nagibni kot, in s tem naklon. To pomaga ne le pri iskanju prave lestvice in gradnji grafov, ampak tudi pri reševanju nekaterih težav v mislih.