Diagonalna kocka: kaj je in kako jo najti?

Diagonala kocke je eden od elementov, ki jih boste morali poznati pri reševanju problemov v stereometriji med zaključkom zaključnega dela iz matematike za potek osnovne šole.

Neka teorija kock

Ta polieder se nanaša neposredno na ravne paralelepipede in prizme. On je poseben primer obeh. Na dnu kocke leži kvadrat, njegovi stranski robovi pa so enaki strani danega kvadrata. Torej vse tri dimenzije imajo enake vrednosti.

Vseh šest obrazov kocke so kvadrati. Dolžina vsakega od 12 robov je enaka.

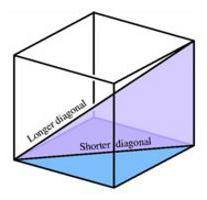
V vsakem obrazu lahko narišete diagonalo, katere dolžino je mogoče najti z uporabo pitagorejske formule. Poleg tega ima sama kocka diagonalo. Samo štiri so. Diagonala kocke je narisana tako, da se začne od vrha spodnje osnove. Konec tega segmenta je na vrhu zgornje osnove, vendar tako, da se ne ujema z diagonalo kvadrata.

Pomembne formule

Vnesti morajo isto oznako. Najpogosteje je črka “a” stran kocke. "V" je prostornina. "S" in "d" sta območje in diagonala. "R" in "r" polmeri opisanih in vpisanih krogel.

V = a³ (# 1) se uporablja za iskanje volumna;

S = a² (# 2) formula za območje obraza;

S = 6a² ( №3 ) je potrebno za izračun površine celotne površine kocke;

če želite vedeti diagonalo kocke, bo formula taka d = a (3 (# 4);

uporabno za iskanje polmerov: R = (a / 2) * √3 in r = a / 2 (št. 5) in (št. 6) .

Nekaj ​​besed o simetriji kocke

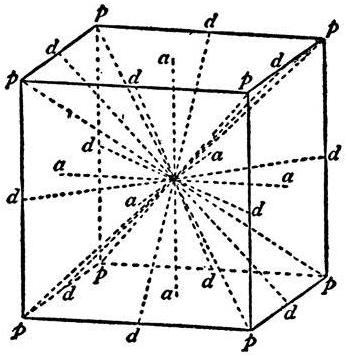
To geometrijsko telo ima dve vrsti simetrije: glede na točko in os. Če želite najti prvo, morate narisati diagonalo kocke, nato drugo, da bi našli točko njihovega presečišča. Bila bo središče simetrije.

Vse črte, ki potekajo skozi to točko in so pravokotne na obraze, so osi simetrije.

Primeri nalog iz izpita

Uporabljajo se v delu B, to je, kjer morate izvesti podrobno rešitev naloge. Samo izberite odgovor tukaj ne bo uspelo. Zato je potrebno poznati formule in jih uporabiti v različnih situacijah.

Prva skupina nalog. Pozna dolžino diagonale kocke. Potrebno je izračunati njegovo prostornino ali ugotoviti površino.

Znana vrednost je lahko na primer enaka eni. Potem, da bi ugotovili, obseg in območje, morate uporabiti formule št. 1 in 3. Ampak oni govorijo o robu, in glede na diagonalo. Napisati boste morali še eno formulo.

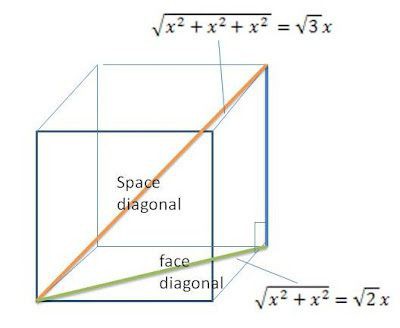
Če pogledate risbo kocke in diagonalno v njem, lahko vidite, katere oblike pravokotni trikotnik. Ena od njegovih nog sovpada z robom, druga z diagonalo obraza, diagonala kocke pa je hipotenuza.

Potem lahko napišemo Pitagorov izrek: kvadrat hipotenuze (d ² ) je enak kvadratu prve noge (a ² ), ki je zložen s kvadratom drugega (a√2) ² . Po izvedenih transformacijah se izkaže, da je rob kocke tako povezan z diagonalo, ki je enaka d, deljena s kvadratnim korenom 3.

Zdaj lahko začnete iskati rob in nato izračunate obseg in območje. Pri določenem problemu je a = 1 / =3 = (√3) / 3. Nato je volumen enak ()3) / 9. Območje je dve.

Druga skupina nalog. Inverzna prejšnja, ko je območje ali obseg znano, in je potrebno izračunati vrednost diagonale kocke.

Primer je problem, pri katerem je površina znana in je enaka 8. Potrebno je uporabiti formulo št. 3 in odvisnost, ki je bila izpeljana iz prejšnjega problema.

Najprej morate vedeti dolžino roba. Je enaka kvadratni koren od delne S do 6. Po zamenjavi znane količine a = √ (8/6) = √ (4/3). Sedaj je ostalo, da izračunamo diagonalo kocke, kvadriramo to število in jo pomnožimo s 3. Izkazalo se je 2.

Tretja skupina nalog vsebuje podatke o diagonali obraza kocke. Spoznati morajo obseg ali področje telesa. Možna je tudi možnost izračuna diagonale kocke. Pri takih težavah je sklepanje sledilo isti poti, kot je bila obravnavana v prejšnjih primerih.