Krog in njegove lastnosti. Obodna dolžina

Obseg matematike je ena najpomembnejših in pomembnejših osebnosti. To je potrebno za različne izračune. Poznavanje lastnosti te številke iz šolskega programa bo zagotovo koristno v življenju. Obseg je potreben pri izračunu več materialov z okroglim prerezom. Naredite risbe, zgradite ograjo v bližini gredice - to bo zahtevalo znanje geometrijska oblika in njegove lastnosti.

Koncept kroga in njegovi glavni elementi

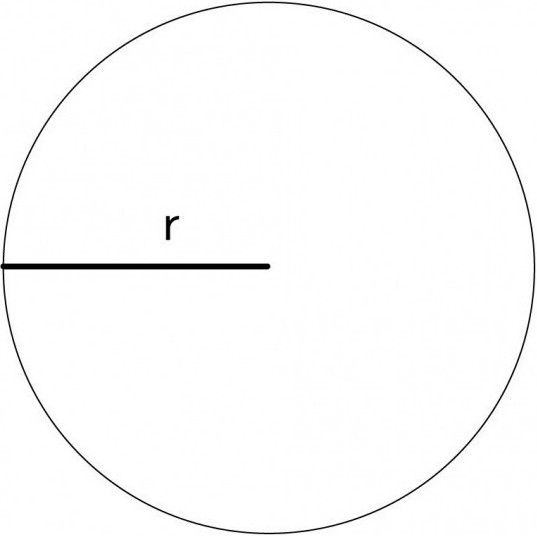
Slika na ravnini, sestavljeni iz številnih točk, ki se nahajajo na enaki razdalji od osrednje, se imenuje krog. Segment, ki zapušča središče in ga povezuje z eno od točk, ki tvorijo krog, se imenuje polmer. Akord je segment, ki med seboj povezuje par točk, ki se nahajajo vzdolž oboda kroga. Če je nameščen tako, da gre skozi osrednjo točko, potem je tudi premer.

Dolžina polmera kroga je enaka dolžini premera, prepolovljena. Par neskladnih točk, ki se nahajajo na krogu, ga razdelimo na dva loka. Če segment s konci na teh točkah poteka skozi osrednjo točko (torej premer), potem bodo oblikovani loki polkrogi.

Območje

Izračun perimetra kroga je določen na več načinov: skozi premer ali preko polmera. V praksi je bilo ugotovljeno, da dolžina kroga (l), kadar je deljena s premerom (d), vedno daje eno število. To število π, ki je enako 3.141692666 ... Izračun se izvede po formuli: π = l / d. S preoblikovanjem dobimo dolžino kroga. Formula je naslednja: l = πd.

Za iskanje polmera uporabite naslednjo formulo: d = 2r. To je omogočila delitev. Konec koncev je polmer polovice premera. Ko dobimo zgoraj navedene vrednosti, lahko izračunamo, kakšna je dolžina kroga po naslednji formuli: l = 2πr.

Osnovne lastnosti

Območje kroga je vedno večje v primerjavi z območji drugih zaprtih krivulj. Tangenta je črta, ki se dotakne kroga samo na eni točki. Če ga črta seka na dveh mestih, potem je sekantna. Točka, ko sta dva različna kroga v stiku drug z drugim, je vedno na ravni črti, ki poteka skozi njihove osrednje točke. Presejanje na ravnini so taki krogi, ki imajo 2 skupni točki. Kot med njimi se izračuna kot kot, ki ga tangente oblikujejo na točke dotika.

Če skozi točko, ki ni točka kroga, narišemo dve ravni črti, ki se nanj ločita, potem bo kot, ki ga oblikujejo, enak razliki v dolžinah lokov, prepolovljenih. To pravilo velja tudi v nasprotnem primeru, ko gre za dva akorda. Dva sekajoča akorda tvorita kot, ki je enak vsoti dolžin lokov, prepolovljenih. V tem vogalu so izbrani loki, v kotu pa nasprotni kot. Optična lastnost kroga se glasi: žarki svetlobe, ki se odbijajo od ogledal, postavljenih okoli oboda kroga, se zberejo nazaj v njegovo središče. V tem primeru mora biti vir svetlobe nameščen v središču kroga.