Osnovni zakoni enosmernega toka: definicije in formule

Ohmov zakon je najprej oblikoval nemški fizik in matematik Georg Simon Om. Ohmov zakon je osnovni zakon za električna vezja z enosmernim tokom. Ugotavlja razmerje med napetostjo ali padcem potenciala, jakostjo toka in uporom v vezju. Oglejmo si podrobneje Ohmov zakon in druge osnovne zakone enosmernega toka.

Zgodovinsko ozadje

Georg Simon Om se je rodil v mestu Erlangen (Nemčija) 16. marca 1789 v protestantski družini. Od zgodnjega otroštva je začel delati v vodovodni delavnici svojega očeta. Fizikalna kariera se je začela v Ommeju na Politehnični univerzi v Nürnbergu. Do konca svojih dni je poučeval fiziko na Univerzi v Münchnu.

Glavna zasluga Ohma v fiziki je, da je uvedel in opisal takšno fizično količino kot električni upor. V matematični obliki je najprej oblikoval razmerje med potencialno razliko, trenutno jakostjo in električnim uporom v vezju, za katero je enota upora poimenovana po njegovem priimku.

Ohmove nove ideje niso takoj sprejele svetovne znanstvene skupnosti, šele leta 1841 je Kraljevo društvo v Londonu podelilo Oomovo medaljo Copley, leta 1849 pa mu je Univerza v Münchnu dodelila Oddelek za fiziko.

Om v času njegove znanstvene dejavnosti se je ukvarjal ne le v električnih vezjih. Leta 1840 je študiral zvočnih valov od leta 1852 se je ukvarjal z optiko, zlasti s pojavom motenj. Znanstvenik je umrl v Münchnu 6. julija 1854.

Ohmovi poskusi

Pred Om je pripravil svoj slavni zakon enosmerni tok drugi znanstveniki so izvedli številne poskuse z električnimi vezji. Opozoriti je treba na poskuse britanskega Henryja Cavendisha, ki je leta 1781 raziskoval vedenje pločevin Leidena, vendar svojih ugotovitev ni mogel objaviti.

Fiziki imajo danes instrumente, ki omogočajo merjenje vseh parametrov električnega tokokroga s potrebno natančnostjo, na koncu 18. in začetku 19. stoletja takih naprav ni bilo, zaradi česar je Ohm težko odkriti zakon za enosmerni tok.

Zato se je Om odločil, da bo takšno napravo naredil sam. Predvsem je uporabil Coulombove torzijske tehtnice, vendar jih je izpopolnil z dodajanjem magnetnega elementa. Istočasno je znanstvenik uporabil odkritje Hansa Christiana Oersteda leta 1819 o dejstvu, da prevodnik s tokom izvaja silo na magnetizirano iglo v bližini njega. S svojim novim torzijskim ravnotežjem, prevodnimi kabli različnih dolžin, izvorom električnega toka in posodami z živim srebrom, je omm lahko izmeril zmanjšanje sile, s katero vodnik s tokom deluje na iglo, ko se dolžina tega vodnika poveča.

Kot rezultat teh poskusov je znanstvenik pridobil naslednjo matematično odvisnost: V = 0,41 lg (1 + x), kjer je V napetost v tokokrogu, x je dolžina prevodnika s tokom. Ta izraz je nato vodil znanstvenika k oblikovanju zakona enosmernega toka.

Koncept moči električnega toka

Pred obravnavo Ohmovega zakona za enosmerni tok uvajamo koncept trenutne moči. Nekateri delci v naravi imajo tako imenovani električni naboj. Koncept trenutne moči je neposredno povezan z gibanjem teh nabitih delcev, ki so večinoma ioni ali elektroni. Tok v fiziki razumemo kot količino naboja, ki prehaja skozi vodnik v enoti časa, kar je matematično izraženo kot naslednji izraz: I = dq / dt.

Enota trenutne jakosti v SI je amper (A), 1 A je jakost toka, pri kateri se naboj 1 C prenese skozi vodnik za 1 s. Ker se pozitivni in negativni naboji gibljejo v nasprotnih smereh v istem električnem polju, je običajno določiti jakost toka s smerjo gibanja pozitivnih nabojev.

Hitrost gibanja nabitih delcev v električnem polju

V fiziki je zakon enosmernega toka formuliran za I = const, kar pomeni, da se mora vsak delec, ki nosi električni naboj, gibati s konstantno hitrostjo. Za obstoj električnega toka pa je potrebno, da so lahko napolnjeni delci sposobni gibanja, kot tudi obstoj električnega polja. Slednji deluje na električni naboj q z določeno silo. Ta sila je določena s formulo: F = q * E, tukaj E je jakost električnega polja.

Po drugem zakonu Newtona nabite delec pridobi pospešek a = q * E / m, kjer je m masa delca. Ker so vse vrednosti v tem izrazu konstantne, bo pospešek tudi konstanten in ne-nič. Vsi ti argumenti so veljavni v primeru, ko se naboj giblje v praznem prostoru, če pa se premika v kateremkoli mediju, potem pride do nekega odpornosti iz medija.

Na primer, elektron, ki se giblje pod vplivom električne sile v kovinskem prevodniku, se srečuje z nenehnimi trki z ioni, ki tvorijo kovinsko kristalno mrežo. Zaradi teh trkov se elektroni premikajo s konstantno hitrostjo, ki se imenuje hitrost odnašanja. V interakciji elektronov z mrežastimi ioni leži narava električnega upora.

Gibanje elektrona v kovinskem vodniku se lahko primerja z gibanjem padca dežja v zraku, saj ta padec ne pada s pospeškom prostega padca, temveč povzroča enakomerno gibanje zaradi vpliva sile upora iz zraka.

Lokalni ohmski zakon

V vsaki šoli se začnejo učiti zakoni DC v 8. razredu. Hkrati oblikovati Ohmov zakon, najprej v lokalni obliki. V ta namen vzemite na primer kovinski vodnik.

V kovini so valenčni elektroni, to je elektroni, ki se nahajajo na zunanjih energetskih lupinah atomov, šibko vezani na atomska jedra, zato v razsutem materialu ne pripadajo določenemu atomskemu jedru, temveč so prosti ali socializirani. Vsak tak elektron pri sobni temperaturi se giblje neurejeno v kovinskem kristalu. To gibanje je podobno gibanju molekule v plinu. Hitrost toplotnega gibanja elektrona je velika, je približno 10 ⁶ m / s. Ker je gibanje enako verjetno v vseh smereh, ne povzroča električnega toka.

Če se ta vodnik nahaja v električnem polju, se pojavi tok. Posledica tega je, da elektron pridobi hitrost drifta, katere velikost je 10 ⁻⁶ m / s. Posledično je električni tok skozi presečno površino A napisan z naslednjo formulo: I = n * q ² * E * t * A / m _e , pri čemer je n število elektronov, ki v času t prehajajo skozi območje A, kar je čas med dva elektronska trka z mrežastimi ioni, m _e - masa elektronov

Nastali izraz lahko ponovno napišemo v obliki J = I / A = σ * E, kjer je J gostota električnega toka, σ je lastnost materiala, ki se imenuje električna prevodnost. Ta izraz za gostoto toka se imenuje Ohmov zakon za enosmerni tok v lokalni obliki.

Ohmov zakon v makroskopski obliki

V šoli v 8. razredu se pravilo enosmernega toka obravnava tudi v makroskopski obliki. Z lahkoto jo je mogoče dobiti iz ustrezne zakonodaje v lokalni obliki. V ta namen je potrebno določiti padec napetosti ali potenciala v električnem tokokrogu kot naslednji izraz: ΔV = E * l, kjer je l dolžina vodnika s tokom, in ΔV je napetost na njenih koncih.

Posledično bo Ohmov zakon dobil obliko: ΔV = I * l / (σ * A) = R * I, kjer je R električni upor. Kot je razvidno iz zakona direktnega električnega toka v makroskopski obliki, je vrednost R inverzna električna prevodnost σ, kar pomeni, da boljši je material, manjši je njegov električni upor. Pomembno je tudi opozoriti, da je σ, čeprav je lastnost materiala, iz katerega je vodnik, R lastnost določenega prevodnika in je odvisna ne le od materiala, temveč tudi od njegovih geometrijskih parametrov (dolžina in območje prereza).

Uporabnost in pomen klasičnega Ohmovega zakona

Ohmov zakon v klasični ali makroskopski obliki je zapisan v obliki: V = I * R. Za kovine je R konstantna vrednost, ne glede na jakost toka, ki poteka skozi prevodnik. Vendar v nekaterih materialih, kot so polprevodniki, ni tako. Materiali, pri katerih je električna upornost konstantna, se imenujejo linearni ali ohmski. Za njih je napetostna funkcija, to je funkcija napetosti kot funkcija toka U (I), linearna.

Ohmskega zakona ni mogoče šteti za temeljni zakon narave, saj velja le za določen razred materialov, predvsem kovin. Vendar ima pomembno vlogo v fiziki in v vsakdanjem življenju, ker nam omogoča, da na preprost način določimo pomembne fizične količine v električnem vezju. Zlasti po zaslugi Ohmovega zakona DC vezje izračuna izgubo električne energije med prenosom in porabo. Ohmov zakon se uporablja tudi za izračun zahtevane vrednosti upora, ki mora biti vključena v električni tokokrog, tako da opravlja svoje funkcije z največjo učinkovitostjo.

Odvisnost odpornosti na temperaturo za ohmske materiale

Glede na zakonitosti enosmernih tokokrogov je treba omeniti, kako se upornost spreminja z naraščanjem temperature. Po analogiji z električno prevodnostjo materiala v fiziki je uveden koncept specifičnega električnega upora ρ, ki je povezan z uporom po naslednji formuli: R = l * ρ / A.

Empirično je bilo ugotovljeno, da za ohmske materiale ρ izpolnjuje naslednjo temperaturno odvisnost: ρ = ρ ₀ * [1 + α (TT ₀ ) + β (TT ₀ ) ² + ...], pri čemer je ρ ₀ specifična upornost tega materiala z temperaturo T ₀ , za katero se pogosto predpostavlja, da je 20 ° C.

Pri kovinskih materialih v območju od 0 do 200 ° C je upornost linearno odvisna od temperature, to je ρ = ρ ₀ * [1 + α (TT ₀ )], pri čemer je α koeficient temperaturne odpornosti, ki je pozitivna vrednost za kovine, kaže, da električna upornost linearno narašča z naraščanjem temperature za kovine. To obnašanje je povezano z zmanjšanjem razdalje, ki jo elektron potuje med dvema trkoma z mrežastimi ioni s povišanjem temperature.

Zanimivo je, da se upornost v polprevodnikih z naraščanjem temperature zmanjšuje. To dejstvo je povezano s povečanjem števila nosilcev električnega toka pri segrevanju polprevodniškega materiala, na primer silicija ali germanija.

Kirchhoffovi zakoni

V šolah v 10. razredu zakoni enosmernega toka niso omejeni na Ohmov zakon. Šolski kurikulum prav tako preučuje zakone Kirchhoffa. Obstajata dva Kirchhoffova zakona za enosmerni tok. Temeljijo na ohranjanje energije in polnjenje v električnem vezju. Naslednje so formulacije za oba Kirchhoffova zakona:

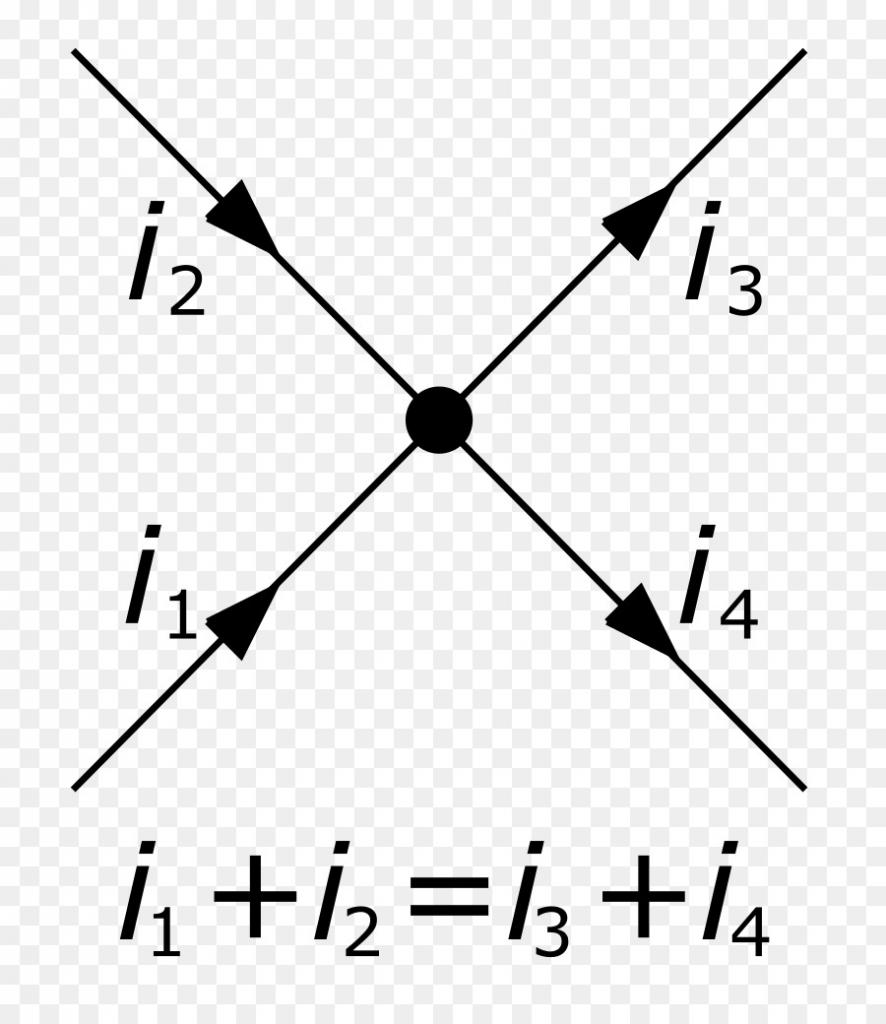
1. Za vsako vozlišče električnega tokokroga je vsota vseh tokov, ki vstopajo v to vozlišče, enaka vsoti tokov, ki ga zapuščajo. Ta formulacija odraža zakon ohranjanja dajatev.
2. V vsakem tokokrogu zaprte zanke je vsota vseh padcev napetosti na elementih tega vezja enaka napetosti, ki ji je napajana. Kirchhoffov drugi zakon odraža ohranjanje potencialne energije v električnem vezju.

Ti zakoni so bili prvič zapisani leta 1846. Trenutno se pogosto uporabljajo v elektrotehniki in elektroniki za določanje neznanih tokov, napetosti in uporov v vezjih. Upoštevajte, da se v primeru prisotnosti ničelnega električnega upora v tokokrogu R del električne energije spremeni v toploto Q, ki se imenuje Joule in se izračuna po formuli Q = I ² Rt, pri čemer je t čas toka, ki teče skozi element vezja z uporom R.

Praktična uporaba Ohmovih in Kirchhoffovih zakonov

Prikazan je primer problema o zakonih enosmernega toka. Spodnja slika prikazuje primer električnega vezja, ki je sestavljen iz dveh tokokrogov, dveh napetostnih virov in 5 uporov z različnimi upori. Naloga je najti neznane tokove I _x in I _y . Takoj je treba povedati, da je smer v obeh konturah izbrana poljubno, v tem primeru v smeri urinega kazalca.

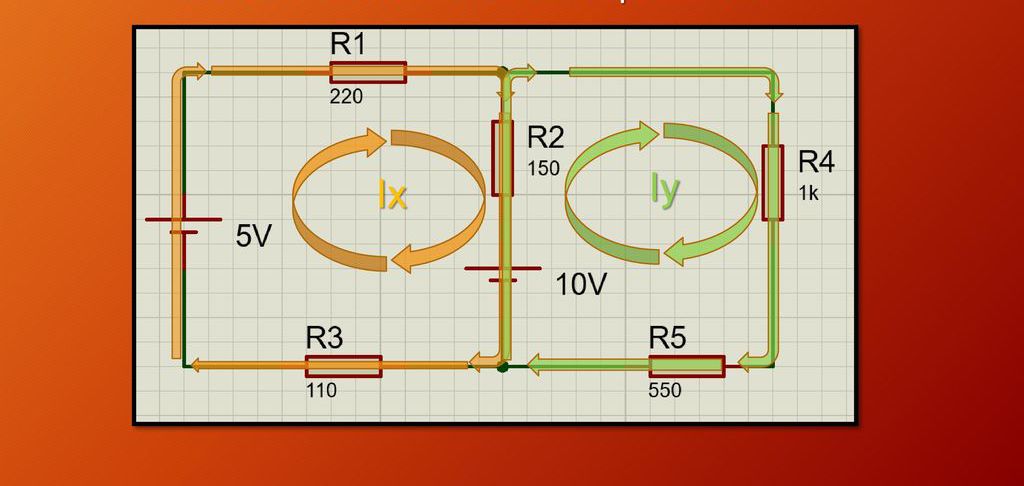
Nato morate upoštevati vsako vezje posebej. Če želite začeti, bodite pozorni na tokokrog z neznanim tokom I _x . Za izbrano vezje je potrebno uporabiti drugi Kirchhoffov zakon, to je zakon, ki pravi, da napetost pade na vseh uporih in napajalna napetost iz vseh tokovnih virov je enaka. Z uporabo tega zakona dobimo: 5-10 = I _x * R ₁ + (I _x -I _y ) * R ₂ + I _x * R ₃ . Pri sestavljanju tega izraza se je upošteval znak izbrane smeri toka I _x kot pozitivne smeri, zato je potencialna razlika pri viru 5 V pozitivna, pri viru 10 V pa negativna. Upoštevajte tudi, da je treba pri obravnavi tega vezja upoštevati tudi tok I _y, ki teče v skladu z vnesenimi simboli skozi upor R2.

Zdaj dobimo podobno enačbo za drugo vezje z neznanim tokom I _y . Ta izraz bo imel obliko: 10 = (I _y -I _x ) * R ₂ + I _y * R ₄ + I _y * R ₅ . V drugem tokokrogu je samo en vir napajanja (10 V), zato le vstopi v izraz, ki izhaja iz 2. Kirchhoffovega zakona.

Tako dobimo dve enačbi, v katerih sta dve neznani: I _x in I _y . Preostalo je združiti te izraze v sistem linearnih enačb in ga rešiti. Spodnja slika prikazuje zadevno vezje in sistem enačb za določanje neznanih tokov.

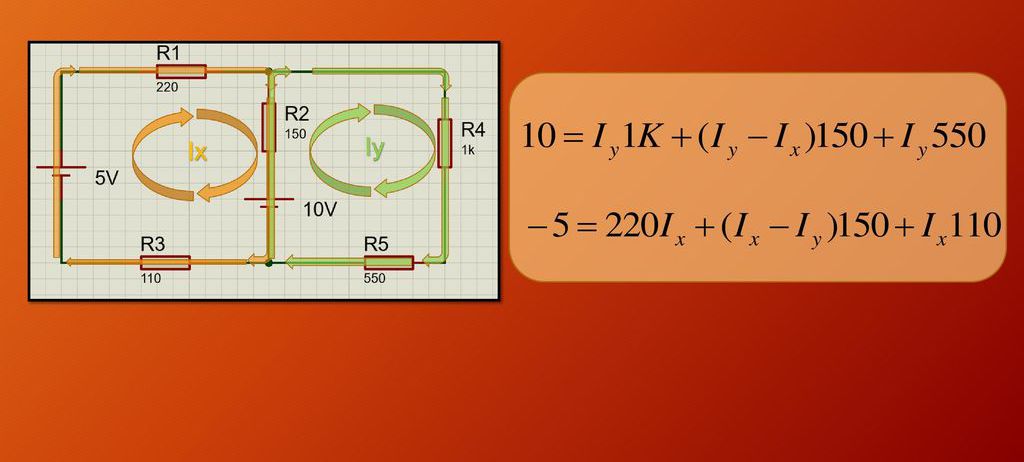
Z reševanjem sistema enačb dobimo, da je I _x = -0,00882 A = -8,82 mA in I _y = 0,0051 A = 5,1 mA. Znak minus kaže, da tok v resnici teče v smeri, ki je nasprotna izbrani. Rezultat je tok 8,82 mA, ki teče skozi upore R ₁ , R ₃ , skozi upore R4, R5 - 5,1 mA in skozi upor R ₂ - I _y - I _x = 13,92 mA.